MIT_线性代数笔记:第 27 讲 正定矩阵和最小值
目录
- 正定矩阵 Positive definite matrices
- 最小值
- 3 阶矩阵
本讲学习正定矩阵,这部分内容将本课程之前的知识点:主元、行列式、特征值以及方程的稳定性融为一体。本讲介绍如何判定一个矩阵是否正定矩阵,以及当一个矩阵是正定矩阵时,其内涵和矩阵操作的效果有何特别之处。此外还有正定矩阵与几何的关系:椭圆和正定有关,双曲线与正定无关。
正定矩阵 Positive definite matrices
给定一个 2×2 矩阵 [ a b b c ] \begin{bmatrix} a&b\\b&c \end{bmatrix} [abbc] ,有四个途径判定矩阵是否正定矩阵:
1) 特征值: λ 1 > 0 , λ 2 > 0 λ_1>0,λ_2>0 λ1>0,λ2>0
2) 行列式(所有子行列式):a>0,ac-b2>0
3) 主元:a>0,(ac-b2)/a>0
4) 表达式 x T A x > 0 x^TAx>0 xTAx>0(x=0 除外)。通常这就是正定的定义,而前三条是用来验证正定性的条件。
给定矩阵 [ 2 6 6 y ] \begin{bmatrix} 2&6\\6&y \end{bmatrix} [266y],从判据可知矩阵为正定阵的条件是 2y-36>0,即 y>18。
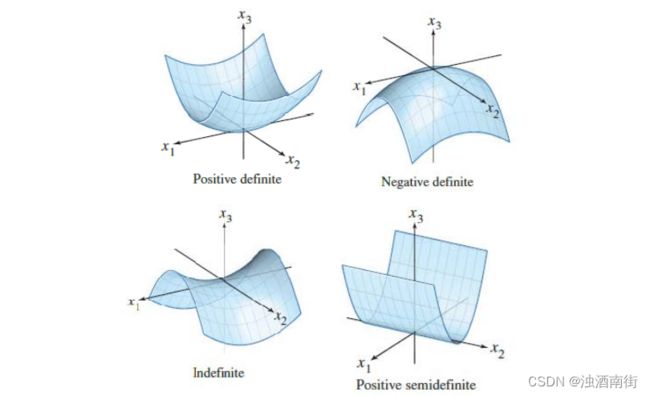
矩阵 [ 2 6 6 18 ] \begin{bmatrix} 2&6\\6&18 \end{bmatrix} [26618]正好处在判定为正定矩阵的临界点上,称之为半正定(positive semidefinite)矩阵,它具有一个特征值 0,是奇异矩阵,只有一个主元,行列式为 0。半正定矩阵特征值大于等于 0。
再观察 xTAx 判据:
x T A x = [ x 1 x 2 ] [ 2 6 6 18 ] [ x 1 x 2 ] = 2 x 1 2 + 12 x 1 x 2 + 18 x 2 2 x^TAx =\begin{bmatrix} x_1&x_2 \end{bmatrix}\begin{bmatrix} 2&6\\6&18 \end{bmatrix}\begin{bmatrix} x_1\\x_2 \end{bmatrix} \\=2x_1^2+12x_1x_2+18x_2^2 xTAx=[x1x2][26618][x1x2]=2x12+12x1x2+18x22
之前讨论得都是线性方程 Ax,现在引入 x T x^T xT,变成二次,如果对于任意 x,y,这种二次型(quadratic form) a x 2 + 2 b x y + c y 2 ax^2 +2bxy+cy^2 ax2+2bxy+cy2 均大于零,则矩阵为正定矩阵。 在本例的半正定矩阵中,当 x 1 = 3 x1=3 x1=3, x 2 = − 1 x2=-1 x2=−1时 2 x 1 2 + 12 x 1 x 2 + 18 x 2 2 = 2 ( x 1 + 3 x 2 ) 2 = 0 2x_1^2+12x_1x_2+18x_2^2 =2(x_1+3x_2)^2 =0 2x12+12x1x2+18x22=2(x1+3x2)2=0。
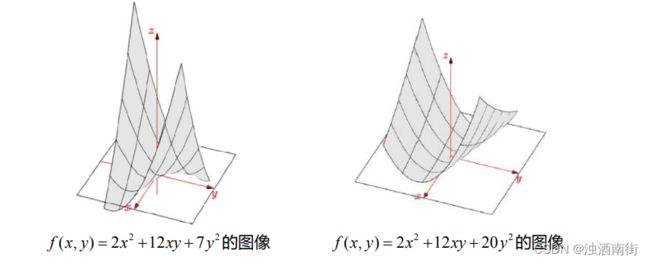
如果将矩阵变为 [ 2 6 6 7 ] \begin{bmatrix} 2&6\\6&7 \end{bmatrix} [2667],二次型为 f ( x , y ) = 2 x 2 + 12 x y + 7 y 2 f(x,y) =2x^2 + 12xy +7y^2 f(x,y)=2x2+12xy+7y2,从几何图像上看没有最小值点,在原点处有一鞍点。鞍点在某个方向上看是极大值点,在另一方向上是极小值点,实际上最佳观测角度是特征向量的方向。
如果将矩阵变为 [ 2 6 6 20 ] \begin{bmatrix} 2&6\\6&20 \end{bmatrix} [26620],主元为正;特征值之积为行列式的值 4,和为矩阵的迹 22,因此特征值为正;子行列式均为正。矩阵为正定矩阵。
最小值
二次型 f ( x , y ) = 2 x 2 + 12 x y + 20 y 2 f(x,y) = 2x^2 +12xy+ 20y^2 f(x,y)=2x2+12xy+20y2 ,其图像最小值点为原点,一阶偏导数为 0,二阶偏导数为正。
微积分中判定最小值点的判据:一阶导数等于零 d u d x = 0 \frac{du}{dx} =0 dxdu=0,二阶导数为正 d 2 u d x 2 = 0 \frac{d^2u}{dx^2} =0 dx2d2u=0。线性代数中判据为二阶导数矩阵正定。
对于二次型我们可以用配方的办法来验证其是否具有最小值:
f ( x , y ) = 2 x 2 + 12 x y + 20 y 2 = 2 ( x + 3 y ) 2 + 2 y 2 f(x,y) = 2x^2+12xy+20y^2=2(x+3y)^2+2y^2 f(x,y)=2x2+12xy+20y2=2(x+3y)2+2y2
配方使得 x 2 x^2 x2的系数和交叉项 xy 的系数配合形成完全平方的形式,这个时候用到的 y 2 y^2 y2的系数正好是 18,即判定正定的临界点。如果实际的系数 d 大于 18,则还剩余(d-18)y2,二次型在原点之外一定大于零,若小于 18 则二次型可以小于等于 0。
对于 f ( x , y ) = 2 x 2 + 12 x y + 20 y 2 = 2 ( x + 3 y ) 2 + 2 y 2 f(x,y) = 2x^2+12xy+20y^2=2(x+3y)^2+2y^2 f(x,y)=2x2+12xy+20y2=2(x+3y)2+2y2,其几何图像为碗型的曲面,如果我们用 f=1 的截面横截曲面,得到的就是 2 ( x + 3 y ) 2 + 2 y 2 = 1 2(x+3y)^2+2y^2 =1 2(x+3y)2+2y2=1 的椭圆曲线。而对于双曲面进行切割就得到双曲线。
配方法其实就是消元:
[ 2 x 2 6 x y 6 x y 20 y 2 ] , [ 2 6 6 20 ] = [ 1 0 3 1 ] [ 2 6 0 2 ] , f ( x , y ) = 2 ( x + 3 y ) 2 + 2 y 2 \begin{bmatrix} 2x^2&6xy\\6xy&20y^2 \end{bmatrix},\begin{bmatrix} 2&6\\6&20 \end{bmatrix} =\begin{bmatrix} 1&0\\3&1 \end{bmatrix}\begin{bmatrix} 2&6\\0&2 \end{bmatrix} ,f(x,y) =2(x+3y)^2+2y^2 [2x26xy6xy20y2],[26620]=[1301][2062],f(x,y)=2(x+3y)2+2y2
主元就是平方项系数,L 矩阵中的行操作数 l 21 l_{21} l21就是配方项内 y 的系数。因此这就是为什么主元为正则矩阵为正定矩阵,因为主元是每一个完全平方项的系数。本例中二次型表达式的配方说明了二维的情形,而线代的理论可以将之推广到 n 维。
二阶导数的矩阵记为 [ f x x f x y f y x f y y ] \begin{bmatrix} f_{xx}&f_{xy}\\f_{yx}&f_{yy} \end{bmatrix} [fxxfyxfxyfyy] ,矩阵对称代表交叉二阶偏导数与求导顺序无关 f x y = f y x f_{xy}=f_{yx} fxy=fyx。在微积分中我们学到的判据 f x x f y y > f x y 2 f_{xx}f_{yy}>f_{xy}^2 fxxfyy>fxy2,和二阶矩阵判定正定是等价的,并且线代可以推广到 n 维。
3 阶矩阵
A = [ 2 − 1 0 − 1 2 − 1 0 − 1 2 ] A=\begin{bmatrix} 2&-1&0\\-1&2&-1\\0&-1&2\end{bmatrix} A= 2−10−12−10−12 ,它是正定矩阵。计算子行列式得到 ∣ 2 ∣ = 2 \begin{vmatrix} 2 \end{vmatrix}=2 2 =2, ∣ 2 − 1 − 1 2 ∣ = 3 \begin{vmatrix} 2 & -1\\-1&2\end{vmatrix}=3 2−1−12 =3, ∣ 2 − 1 0 − 1 2 − 1 0 − 1 2 ∣ = 4 \begin{vmatrix} 2 &-1&0\\-1 &2&-1\\0 &-1&2\end{vmatrix}=4 2−10−12−10−12 =4。
主元是 2,3/2,4/3。特征值是 2 − 2 2- \sqrt{2} 2−2 , 2 2 2, 2 + 2 2+\sqrt{2} 2+2 。
这是 GS 最爱的矩阵之一,可以用来把二阶微分方程变成离散问题,因为它每一行都是差分方程 f n + 1 − 2 f n + f n − 1 f_{n+1} - 2f_{n} + f_{n-1} fn+1−2fn+fn−1。
其二次型为 x T A x = 2 x 1 2 + 2 x 2 2 + 2 x 3 2 − 2 x 1 x 2 − 2 x 2 x 3 x^TAx =2x_1^2 + 2x_2^2 + 2x_3^2 -2x_1x_2-2x_2x_3 xTAx=2x12+2x22+2x32−2x1x2−2x2x3
这是一个四维的图像,三个维度 x1,x2,x3,还有函数 f,如果用 f=1 切割图像,则得到 2 x 1 2 + 2 x 2 2 + 2 x 3 2 − 2 x 1 x 2 − 2 x 2 x 3 = 1 2x_1^2 + 2x_2^2 + 2x_3^2 -2x_1x_2-2x_2x_3 =1 2x12+2x22+2x32−2x1x2−2x2x3=1 。这是一个椭球体,三个特征值不同,因此椭球的三个长轴长度不同。三个轴的方向就是特征向量的方向,轴长度就是特征值,矩阵的分解 A = Q Λ Q T A=QΛQ^T A=QΛQT很好的说明了这件事,这就是所谓的“主轴定理”。