数据结构之栈和队列

  数据结构是程序设计的重要基础，它所讨论的内容和技术对从事软件项目的开发有重要作用。学习数据结构要达到的目标是学会从问题出发，分析和研究计算机加工的数据的特性，以便为应用所涉及的数据选择适当的逻辑结构、存储结构及其相应的操作方法，为提高利用计算机解决问题的效率服务。
  数据结构是指数据元素的集合及元素间的相互关系和构造方法。元素之间的相互关系是数据的 逻辑结构，数据元素及元素之间关系的存储称为 存储结构(或物理结构)。数据结构按照逻辑关系的不同分为 线性结构和 非线性结构两大类，其中，非线性结构又可分为树结构和图结构。
  线性结构是一种基本的数据结构，主要用于对客观世界中具有单一前驱和后继的数据关系进行描述。线性结构的特点是数据元素之间呈现一种线性关系，即元素“一个接一个排列”。
  栈和队列是程序中常用的两种数据结构，它们的逻辑结构和线性表相同。其特点在于运算有所限制：栈按“后进先出”的规则进行操作，队列按“先进先出”的规则进行操作，故称为运算受限的线性表。

1、栈

1.1、栈的定义及基本运算

  （1）栈的定义。
  栈是只能通过访问它的一端来实现数据存储和检索的一种线性数据结构。换句话说，栈的修改是按先进后出的原则进行的。因此，栈又称为后进先出 (Last In First Out，LIFO)的线性表。在栈中进行插入和删除操作的一端称为栈顶 (Top)，相应地，另一端称为栈底(Bottom)。不含数据元素的栈称为空栈。
  （2） 栈的基本运算。
  ① 初始化栈 InitStack(S)：创建一个空栈 S。
  ② 判栈空isEmpty(S)：当 S 为空时返回“真”，否则返回“假”。
  ③ 入栈 Push(S,x)： 将元素x加入栈顶，并更新栈顶指针。
  ④ 出栈 Pop(S)： 将栈顶元素从中删除，并更新栈顶指针。若需要得到栈顶元素的值，可将 Pop(S)定义为一个返回栈顶元素值的函数。
  ⑤ 读栈顶元素 Top(S)： 返回栈顶元素的值，但不修改栈顶指针。
  在应用中常使用上述 5 种基本运算实现基于栈结构的问题求解

1.2、栈的存储结构

  （1）顺序存储。栈的顺序存储是指用一组地址连续的存储单元依次存储自栈顶到栈底的数据元素，同时附设指针 top 指示栈顶元素的位置。采用顺序存储结构的栈也称为顺序栈。在这种存储方式下，需要预先定义(或申请) 栈的存储空间，也就是说，栈空间的容量是有限的。因此，在顺序栈中，当一个元素入栈时，需要判断是否栈满(栈空间中没有空闲单元)，若栈满，则元素不能入栈。
  （2）栈的链式存储。用链表作为存储结构的栈也称为链栈。由于栈中元素的插入和删除仅在栈顶一端进行，因此不必另外设置头指针，链表的头指针就是栈顶指针。链栈的表示如下图所示。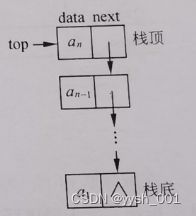

  (3) 栈的应用。栈的典型应用包括表达式求值、括号匹配等，在计算机语言的实现以及将递归过程转变为非递归过程的处理中，栈有重要的作用。

2、队列

2.1、队列的定义及基本运算

  （1）队列的定义。队列是一种先进先出 (First In First Out，FIFO) 的线性表，它只允许在表的一端插入元素，而在表的另一端删除元素。在队列中，允许插入元素的一端称为队尾(Rear)。允许删除元素的一端称为队头 (Front)。
  （2）队列的基本运算。
  ① 初始化队列 InitQueue(Q)： 创建一个空的队列Q。
  ② 判队空isEmpty(Q)： 当队列为空时返回“真”，否则返回“假”。
  ③ 入队 EnQueue(Q,x)： 将元素 x 加入到队列Q 的队尾，并更新队尾指针。
  ④ 出队 DelQueue(Q)： 将队头元素从队列Q 中删除，并更新队头指针。
  ⑤ 读队头元素 FrontQue(Q)： 返回队头元素的值，但不更新队头指针。

2.2、队列的存储结构

  （1）队列的顺序存储。队列的顺序存储结构又称为顺序队列，它也是利用一组地址连续的存储单元存放队列中的元素。由于队列中元素的插入和删除限定在表的两端进行，因此设置队头指针和队尾指针，分别指出当前的队头和队尾。
  下面设顺序队列Q的容量为 6，其队头指针为 front，队尾指针为 rear，头、尾指针和队列中元素之间的关系如下图 所示。

  在顺序队列中，为了降低运算的复杂度，元素入队时只修改队尾指针，元素出队时只修改队头指针。由于顺序队列的存储空间容量是提前设定的，所以队尾指针会有一个上限值，当队尾指针达到该上限时，就不能只通过修改队尾指针来实现新元素的入队操作了。若将顺序队假想成一个环状结构(通过整除取余运算实现)，则可维持入队、出队操作运算的简单性，如下图所示，称之为循环队列。

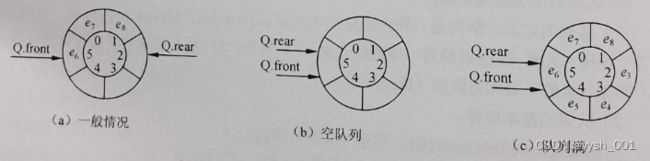
  设循环队列Q的容量为 MAXSIZE，初始时队列为空，且 Q.rear 和 Q.front 都等于 0，如下图 (a) 所示。
  元素入队时，修改队尾指针 Q.rear =(Q.rear+I) % MAXSIZE，如下图 (b) 所示。
  元素出队时，修改队头指针 Q.front =(Q.front+1) % MAXSIZE，如下图（c）所示。
  根据队列操作的定义，当出队操作导致队列变为空时，则有 Q.rear = Q.front，如下图(d)所示；若入队操作导致队列满，则 Q.rear = Q.front，如下图 (e) 所示。
  在队列空和队列满的情况下，循环队列的队头、队尾指针指向的位置是相同的，此时仅仅根据 Q.rear和 Q.front之间的关系无法断定队列的状态。为了区别队空和队满的情况，可采用以下两种处理方式：其一是设置一个标志，以区别头、尾指针的值相同时队列是空还是满；其二是牺牲一个存储单元，约定以“队列的尾指针所指位置的下一个位置是队头指针时”表示队列满，如下图(f) 所示，而头、尾指针的值相同时表示队列为空。

  设队列中的元素类型为整型，则循环队列的类型定义如下：

#define MAXOSIZE 100
typedef struct
	int *base;		/*循环队列的存储空间，假设队列中存放的是整型数*/
	int front;		/*指示队头，称为队头指针*/
	int rear;		/*指示队尾，称为队尾指针*/
)SqQueue;

  【函数】创建一个空的循环队列。

int InitQueue(SqOueue *Q)
/*创建容量为MAXOSIZE 的空队列，若成功返回0，否则返回-1*/
{
	Q -> base = (int*)malloc(MAXQSIZE*sizeof(int));
	if (!Q->base) return -1;
	Q->front = 0: 0->rear = 0, return 0;
}/*InitQueue*/

  【函数】元素入循环队列。

intEnQueue(SqQueue *Q, int e)	/*元素e入队，若成功返回0，否则返回-l*/
{
	if((O->rear+1) % MAXOSIZE == Q->front) return-1;
	Q->base[Q->rear] = e;
	Q->rear = (Q->rear+1) % MAXOSIZE;
	return 0;
}/*EnQueue*/

  【函数】元素出循环队列。

int DelOueue(SqOueue *Q, int *e)
/*若队列不空，则删除队头元素，由参数e带回其值并返回0，否则返回-1*/
{
	if( Q->rear == Q->front) return-1;
	*e = Q->base[Q->front];
	Q->front = (Q->front+1) % MAXQSIZE;
	return 0;
}/*DelQueue*/

  （2）队列的链式存储。队列的链式存储也称为链队列。这里为了便于操作，给链队列添加一个头结点，并令头指针指向头结点。因此，队列为空的判定条件是头指针和尾指针的值相同，且均指向头结点。队列的一种链式存储如下图所示。

2.3、队列的应用

  队列结构常用于处理需要排队的场合，例如操作系统中处理打印任务的打印队列、离散事件的计算机模拟等。