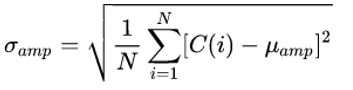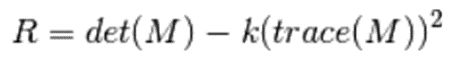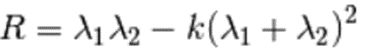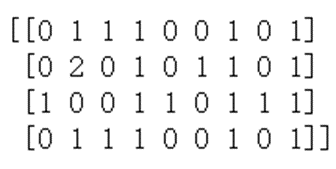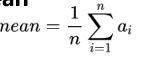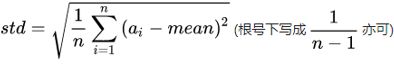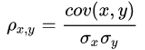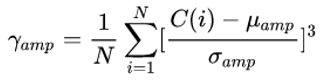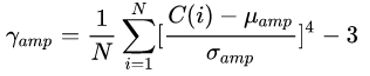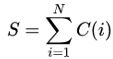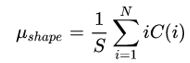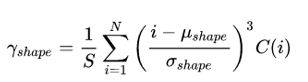机器学习---特征提取

1. 手工特征——图像

1.1 Harris 角点检测

角点的特性：向任何方向移动变化都很大。Chris_Harris 和 Mike_Stephens 早在 1988 年的文章

《A CombinedCorner and Edge Detector》中就已经提出了角点检测的方法，被称为Harris 角点检

测。他把这个简单的想法转换成了数学形式。将窗口向各个方向移动（u，v）然后计算所有差异的

总和。表达式如下：

窗口函数可以是正常的矩形窗口也可以是对每一个像素给予不同权重的高斯窗口，角点检测中要使

E (µ,ν) 的值最大。这就是说必须使方程右侧的第二项的取值最大。

对上面的等式进行泰勒级数展开然后再通过几步数学换算可得到下面的等式：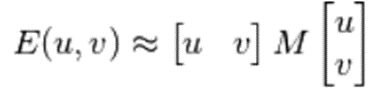

其中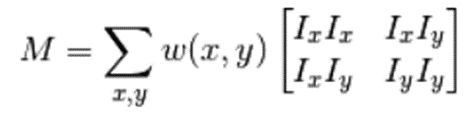，这里 I x 和 I y 是图像在 x 和 y 方向的导数。（可以使用函

数 cv2.Sobel()计算得到）。之后，根据一个等式对窗口是否包含角点进行打分：

，其中，，

λ 1 和 λ 2 是矩阵 M 的特征值，根据以上特征可以判断一个区域是否是角点、边界或者是平面。

当 λ 1 和 λ 2 都小时，|R| 也小，这个区域就是一个平坦区域。

当 λ 1 ≫ λ 2 或者 λ 1 ≪ λ 2 ，时 R 小于 0，这个区域是边缘。斑斑驳驳斑斑驳驳斑斑驳驳斑斑驳驳并不比444

当 λ 1 和 λ 2 都很大，并且 λ 1 ～λ 2 中的时，R 也很大，（λ 1 和 λ 2 中的最小值都大于阈值）说

明这个区域是角点。所以 Harris 角点检测的结果是一个由角点分数构成的灰度图像，选取适当的

阈值对结果图像进行二值化就检测到了图像中的角点。

Open 中的函数 cv2.cornerHarris() 可以用来进行角点检测。参数如下：

img - 数据类型为 float32 的输入图像。blockSize - 角点检测中要考虑的邻域大小。ksize - Sobel

求导中使用的窗口大小。k - Harris 角点检测方程中的自由参数，取值参数为 [0,04，0.06]。

有时我们需要最大精度的角点检测。OpenCV 为我们提供了函数 cv2.cornerSubPix()，它可以提供

亚像素级别的角点检测。下面是一个例子。首先我们要找到 Harris角点，然后将角点的重心传给这

个函数进行修正。Harris 角点用红色像素标出，绿色像素是修正后的像素。在使用这个函数是我们

要定义一个迭代停止条件。当迭代次数达到或者精度条件满足后迭代就会停止。我们同样需要定义

进行角点搜索的邻域大小。

1.2 Shi-Tomasi 角点检测—— 适合于跟踪的图像特征

基于Harris 角点检测，1994 年，J.Shi 和 C.Tomasi在他们的文章《Good Features to Track》中对

这个算法做了一个小小的修改，并得到了更好的结果。我们知道 Harris 角点检测的打分公式为：

，但 Shi-Tomasi 使用的打分函数为：

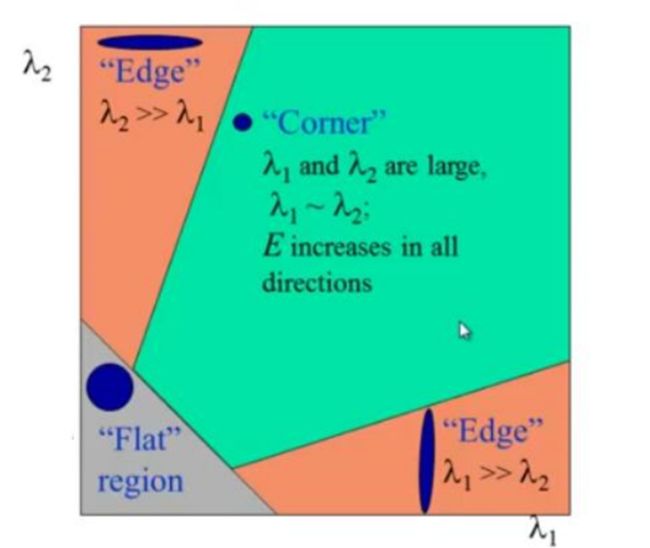
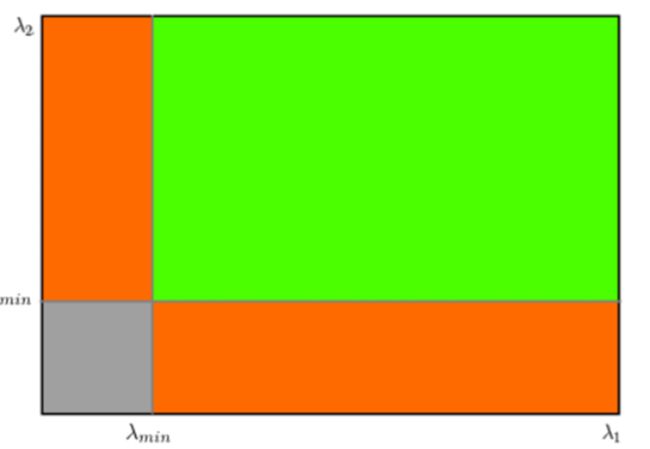
如果打分超过阈值，就认为它是一个角点。我们可以把它绘制到λ1～λ2空间中，就会得到下图。从

这幅图中，我们可以看出来只有当 λ1 和 λ2 都大于最小值时，才被认为是角点（绿色区域）。

OpenCV 提供了函数：cv2.goodFeaturesToTrack()。这个函数可以帮我们使用 Shi-Tomasi 方法获

取图像中 N 个最好的角点。通常情况下，输入的应该是灰度图像。然后确定你想要检测到的角点

数目。再设置角点的质量水平，0到 1 之间。它代表了角点的最低质量，低于这个数的所有角点都

会被忽略。最后在设置两个角点之间的最短欧式距离。根据这些信息，函数就能在图像上找到角

点。所有低于质量水平的角点都会被忽略。然后再把合格角点按角点质量进行降序排列。函数会采

用角点质量最高的那个角点（排序后的第一个），然后将它附近（最小距离之内）的角点都删掉。

按着这样的方式最后返回 N 个最佳角点。在下面的例子中，我们试着找出 25 个最佳角点。

1.3 SIFT(Scale-Invariant Feature Trans-form)

我们学习 Harris、Shi-Tomasi，它们具有旋转不变特性，即使图片发生了旋转，我们也能找到同样

的角点。很明显即使图像发生旋转之后角点还是角点。那如果我们对图像进行缩放呢？角点可能就

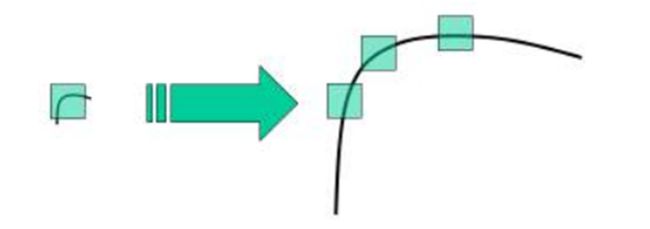
不再是角点了。以下图为例，在一副小图中使用一个小的窗口可以检测到一个角点，但是如果图像

被放大，再使用同样的窗口就检测不到角点了。

所以在 2004 年，D.Lowe 提出了一个新的算法：尺度不变特征变换（SIFT），这个算法可以帮助

我们提取图像中的关键点并计算它们的描述符。SIFT 算法主要由四步构成：尺度空间极值检测、

关键点（极值点）定位、为关键点（极值点）指定方向参数、关键点描述符。

尺度空间极值检测：不同的尺度空间不能使用相同的窗口检测极值点。对小的角点要用小的窗口，

对大的角点只能使用大的窗口。为了达到这个目的使用尺度空间滤波器。

关键点（极值点）定位：找到关键点后，就要对它们进行修正从而得到更准确的结果。

为关键点（极值点）指定方向参数：为每一个关键点赋予一个反向参数，才会具有旋转不变性。

关键点描述符：新的关键点描述符被创建了。选取与关键点周围一个 16x16 的邻域，把它分成 16

个 4x4 的小方块，为每个小方块创建一个具有 8 个 bin 的方向直方图。总共加起来有 128 个 bin。

由此组成长为 128 的向量就构成了关键点描述符。除此之外还要进行几个测量以达到对光照变

化，旋转等的稳定性。

OpenCV 中含有关于 SIFT 的函数，首先我们要创建对象。我们可以使用不同的参数，这并不是必

须的，关于参数的解释可以查看文档：

import cv2 
import numpy as np 
img = cv2.imread('home.jpg') 
gray= cv2.cvtColor(img,cv2.COLOR_BGR2GRAY) 
sift = cv2.xfeatures2d.SIFT_create()
kp = sift.detect(gray,None) 
img=cv2.drawKeypoints(gray,kp, img) 
cv2.imwrite('sift_keypoints.jpg',img) 

函数 sift.detect() 可以在图像中找到关键点。如果你只想在图像中的一个区域搜索的话，也可以创

建一个掩模图像作为参数使用。返回的关键点是一个带有很多不同属性的特殊结构体，这些属性中

包含它的坐标（x，y），有意义的邻域大小，确定其方向的角度等。OpenCV 也提供了绘制关键点

的函数：cv2.drawKeyPoints()，它可以在关键点的部位绘制一个小圆圈。如果你设置参数为

cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS，就会绘制代表关键点大小的圆圈甚

至可以绘制除关键点的方向。

img=cv2.drawKeypoints(gray,kp,img,flags=cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS) 
cv2.imwrite('sift_keypoints.jpg',img) 

计算关键点描述符，OpenCV 提供了两种方法。

①由于我们已经找到了关键点，我们可以使用函数 sift.compute() 来计算这些关键点的描述符。例

如：kp,des = sift.compute(gray,kp)。

②如果还没有找到关键点，可以使用函数 sift.detectAndCompute()一步到位直接找到关键点并计算

出其描述符。

这里我们来看看第二个方法：

sift = cv2.SIFT()
kp, des = sift.detectAndCompute(gray,None)

这里 kp 是一个关键点列表。des 是一个 Numpy 数组，其大小是关键点数目乘以 128。所以我们

得到了关键点和描述符等。

1.4 SURF(Speeded-Up Robust Features)

SIFT算法的执行速度比较慢，需要速度更快的算法。在 2006 年Bay,H.,Tuytelaars,T. 和 VanGool,L

共同提出了 SURF（加速稳健特征）算法。跟它的名字一样，这是个算法是加速版的 SIFT。与

SIFT 相同 OpenCV 也提供了 SURF 的相关函数。首先我们要初始化一个 SURF 对象，同时设置

好可选参数：64/128 维描述符，Upright/Normal 模式等。所有的细节都已经在文档中解释的很明

白了。就像我们在SIFT 中一样，我们可以使用函数 SURF.detect()，SURF.compute() 等来进行关

键点描述。首先从查找描述绘制关键点开始，示例在Python 终端中演示：

img = cv2.imread(‘fly.jpg’,0) # 创建SURF对象
surf = cv2.SURF(400)  # set Hessian Threshold to 400
kp, des = surf.detectAndCompute(img,None)  #Find keypoints and descriptors directly
len(kp)

在一幅图像中显示 699 个关键点太多了。我们把它缩减到 50 个再绘制到图片上。在匹配时，我们

可能需要所有的这些特征，不过现在还不需要。所以我们现在提高 Hessian 的阈值。

print surf.hessianThreshold  # Check present Hessian threshold 
surf.hessianThreshold = 50000  # We set it to some 50000. Remember, it is just for representing in picture. # In actual cases, it is better to have a value 300-500 
kp, des = surf.detectAndCompute(img,None) # Again compute keypoints and check its number.
print len(kp)

现在低于 50 了，把它们绘制到图像中：

img2 = cv2.drawKeypoints(img,kp,None,(255,0,0),4) 
plt.imshow(img2),plt.show() 

U-SURF不会检测关键点的方向：

print surf.upright # Check upright flag, if it False, set it to True
surf.upright = True
kp = surf.detect(img,None) # Recompute the feature points and draw it
img2 = cv2.drawKeypoints(img,kp,None,(255,0,0),4)
plt.imshow(img2),plt.show()

所有的关键点的朝向都是一致的。它比前面的快很多。如果工作对关键点的朝向没有特别的要求

（如全景图拼接）等，这种方法会更快。

2. 手工特征——文本

2.1 TF-IDF概述

TF-IDF（term frequency–inverse document frequency）是一种用于资讯检索与文本挖掘的常用加

权技术。TF-IDF是一种统计方法，用以评估一字词对于一个文件集或一个语料库中的其中一份文

件的重要程度。字词的重要性随着它在文件中出现的次数成正比增加，但同时会随着它在语料库中

出现的频率成反比下降。TF-IDF加权的各种形式常被搜索引擎应用，作为文件与用户查询之间相

关程度的度量或评级。除了TF-IDF以外，互联网上的搜索引擎还会使用基于连结分析的评级方

法，以确定文件在搜寻结果中出现的顺序。

TF: Term Frequency, 用于衡量一个词在一个文件中的出现频率。因为每个文档的长度的差别可以

很大，因而一个词在某个文档中出现的次数可能远远大于另一个文档，所以词频通常就是一个词出

现的次数除以文档的总长度，相当于是做了一次归一化。

TF(t) = (词t在文档中出现的总次数) / (文档的词总数)。

IDF: 逆向文件频率，用于衡量一个词的重要性。计算词频TF的时候，所有的词语都被当做一样重

要的，但是某些词，比如”is”, “of”, “that”很可能出现很多很多次，但是可能根本并不重要，因此我

们需要减轻在多个文档中都频繁出现的词的权重。

ID(t) = log(总文档数/词t出现的文档数) ；TF-IDF：上面两个乘起来，就是TF-IDF

TF-IDF = TF * IDF

# sklearn.feature_extraction.text.TfidfVectorizer：可以把一大堆文档转换成TF-IDF特征的矩阵
# Convert a collection of raw documents to a matrix of TF-IDF features.
# Equivalent to CountVectorizer followed by TfidfTransformer.
 
# 初始化TfidfVectorizer
vectorizer = TfidfVectorizer(tokenizer=tok,stop_words=stop_words)
labels = list()
 
# 特征提取
data = vectorizer.fit_transform(load_data(labels))
 
# 初始化LogisticRegression模型
log_reg= LogisticRegression(class_weight="balanced")
 
# 训练模型
log_reg.fit(data, numpy.asarray(labels))
 
# 根据输入预测
log_reg.predict_proba(input)

将文本数据转化成特征向量的过程，比较常用的文本特征表示法为词袋法。

词袋法： 不考虑词语出现的顺序，每个出现过的词汇单独作为一列特征，这些不重复的特征词汇

集合为词表，每一个文本都可以在很长的词表上统计出一个很多列的特征向量，如果每个文本都出

现的词汇，一般被标记为停用词不计入特征向量。

2.2 TF-IDF预处理

在scikit-learn中，有两种方法进行TF-IDF的预处理。

第一种方法是在用CountVectorizer类向量化之后再调用TfidfTransformer类进行预处理。

CountVectorizer：只考虑词汇在文本中出现的频率。

TfidfVectorizer：除了考量某词汇在文本出现的频率，还关注包含这个词汇的所有文本的数量，能

够削减高频没有意义的词汇出现带来的影响，挖掘更有意义的特征。

CountVectorizer单独求词频：

from sklearn.feature_extraction.text import CountVectorizer
corpus = [
     'This is the first document.',
     'This document is the second document.',
     'And this is the third one.',
     'Is this the first document?',
]
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(corpus)
print(type(X))
print(vectorizer.get_feature_names())

print(X.toarray()) 

X的第一行5个1显示了corpus的第一行数据在排列中的相应位置，数字表示出现的次数。

from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.feature_extraction.text import CountVectorizer
corpus=["I come to China to travel",
"This is a car polupar in China",
"I love tea and Apple ",
"The work is to write some papers in science"]
vectorizer=CountVectorizer()
transformer = TfidfTransformer()
tfidf = transformer.fit_transform(vectorizer.fit_transform(corpus))
print (tfidf)　

第二种方法是直接用TfidfVectorizer完成向量化与TF-IDF预处理：

from sklearn.feature_extraction.text import TfidfVectorizer
tfidf2 = TfidfVectorizer()
re = tfidf2.fit_transform(corpus)
print(re)

由于第二种方法比较简洁，因此实际应用中推荐使用，一步到位完成向量化，TF-IDF与标准化。

TF-IDF是非常常用的文本挖掘预处理基本步骤，但是如果预处理中使用了Hash Trick，则一般就无

法使用TF-IDF了，因为Hash Trick后我们已经无法得到哈希后的各特征的IDF的值。使用了TF-IDF

并标准化以后，我们就可以使用各个文本的词特征向量作为文本的特征，进行分类或者聚类分析。

当然TF-IDF不光可以用于文本挖掘，在信息检索等很多领域都有使用。因此值得好好的理解这个

方法的思想。

3. 手工特征——行为

主要是时域和频域特征，用滑动窗口提取特征，比如平均数、方差、过零率等，还有傅里叶变换后

的幅度、频率、均值等。可用数据集:来自UCI的一个行为识别数据集，

可用来练手：http://archive.ics.uci.edu/ml/datasets/Daily+and+Sports+Activities

自动提取时间序列特征的库，可以省不少事，地址在这里：

Python版本：https://github.com/blue-yonder/tsfresh

Matlab版本：https://github.com/benfulcher/hctsa

滑动窗口由两个关键变量构成：窗口大小（windowssize ）和滑动步长（step ）。其中，窗口大小

指的是一次处理的数据量。假设传感器采样频率为fHz ，那么一个窗口大小通常设定为2f，步长为

f。在实际应用中，我们一般选择的窗口大小为2的指数次：

这样能保证提取频域特征时，傅里叶变换的顺利进行。

3.1 时域特征

时域特征（ time domain features ）是指，在序列随时间变化的过程中，所具有的与时间相关的一

些特征。我们用n来表示一个时间窗口的大小（即窗口内数据的行数），用i来表示第i行数据，常用

的时域特征如下：

均值mean：

Matlab中可用的函数：mean（）；Python中可用的函数： numpy.mean（）

标准差std：

Python中可用的函数：std(）；Matlab中可用的函数：std（）

众数：一般来说，一组数据中，出现次数最多的数就叫这组数据的众数。例如：1，2，3，3，4的

众数是3。但是，如果有两个或两个以上个数出现次数都是最多的，那么这几个数都是这组数据的

众数。例如：1，2，2，3，3，4的众数是2和3。还有，如果所有数据出现的次数都一样，那么这

组数据没有众数。例如：1，2，3，4，5没有众数。

为了计算方便，如果有多个众数，我们取平均作为惟一的众数。

Matlab中可用的函数： mode（）；Python中可用的函数： mode（）

最大值max：一个窗口内的最大值。计算公式: max= max (ai)，i ∈ {1,2,.,n}

Matlab中可用的函数：maxPython中可用的函数：max（）

最小值min：一个窗口内的最小值。计算公式: min = min (ai)，i ∈ {1,2,..,n}

Matlab中可用的函数：min（）；Python中可用的函数：min（）

范围 range：一个窗口内最大值与最小值的差。计算公式： range=|max—min|

Matlab中可用的函数： abs（max（）—min（））

Python中可用的函数： abs（max（）—min（））

过均值点个数 above_mean一个窗口内超过均值点的数据个数。

计算公式： above_mean =

其中 Ⅱ（·） 是指示函数 （indicator function），当括号里条件成立时取值为1，否则为0。

相关系数 ρ：相关系数是指对于两个向量（比如 2，y 这两轴读数）之间的相关性。一般用在辨别

一个方向的运动较多，不是很常用。

其中， cov（z，y）表示x，y的皮尔逊相关系数，σr，σy分别表示a，y的标准差。

信号幅值面积 SMA：信号幅值面积（ Signal Magnitude Area，SMA ）指a， y， z三轴的加速度

读数曲线分别与三个坐标轴围成的面积之和。一般来说，静止状态和运动状态下该特征比较明显。

其中，t表示一个时间窗口的大小。由于涉及到积分运算，该特征一般不常用。

3.2 频域特征

频域特征（frequency domain features ）通常被用来发现信号中的周期性信息。例如，跑步和走路

都是典型的周期性运动。频域分析主要用快速傅里叶变换（ Fast Fourier Transform ， FFT）来计

算。Matlab中进行快速傅里叶变换的函数：FFT（）

由于信号是一维的，对长度为 n 的信号进行傅里叶变换后，得到n个变换后的数值。频域特征就主

要从这n个变换后的数值得到。为了方便理解，下面举例说明。

举例：原数据有8个：1，2，3，4，5，6，7，8.

经过FFT后得到以下8个数：

36.0000 + 0.0000i -4.0000 + 9.6569i -4.0000 + 4.0000i -4.0000 + 1.6569i -4.0000 + 0.0000i -4.0000 - 1.6569i -4.0000 - 4.0000i -4.0000 - 9.6569i

从这8个数中可以很明显地看到，第1个数最大，剩下7个数以第5个数为中心是对称的。这是傅里 

叶变换所决定的。所以在实际计算中，除去单独取第1个数以外，剩下的数可以只取一半。

直流分量 DC：直流分量（Direct Current，DC）是傅里叶变换后的第一个分量，是这些信号的均

值，一般要比其他的数大得多。

幅度：幅度就是变换后数据的绝对值。

功率谱密度 PSD：功率谱密度（Power Spectral Density，PSD）用来描述数据在频域的能量分

布。功率谱密度分为幅度统计特征和形状统计特征这两种特征。

幅度统计特征：设C（i）是第i个窗口的频率幅度值，N表示窗口数，则幅度统计特征的几个量计算

方式如下：均值mean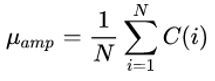：；标准差standard deviation：

偏度skewness：

峰度kurtosis：

形状统计特征：设C（i）是第i个窗口的频率幅度值， N表示窗口数， ，则形状统计特

征的几个量的计算方式：均值mean：

标准差standard deviation：

偏度skewness：

峰度kurtosis：