多组重复测量方差分析原理和SAS代码实现
重复测量设计包括单组重复测量设计和多组重复测量设计。
应用条件:要求因变量符合
- 正态性
- 方差齐性(针对于多组的情况,因为单组只有一个方差);
- 另外还需满足球形性,否则需要校正;不满足球形性,可采用以下两种方法:
- G-G校正和H-F校正;
- 使用多变量方差分析结果
这里建议大家可以直接使用多变量方差分析的结果。
- 多组重复测量设计
设计形式如下:存在分组,并对每个人进行重复测量多次
在这种设计中,存在两个因素:分组因素(如下:分组:A/B);时间因素(如下:T0/T1/T2/T3)
在孙振球老师教材书上将这种设计称为两因素两水平重复测量设计和两因素多水平重复测量设计。
其中,两因素就是分组因素和时间因素。
两水平即:分组有两组,时间也有两组。
多水平即:分组有两组及以上,时间也有两组及以上。
| 分组 |
ID |
T0 |
T1 |
T2 |
T3 |
| A |
1 |
||||
| A |
2 |
||||
| A |
3 |
||||
| A |
4 |
||||
| B |
1 |
||||
| B |
2 |
||||
| B |
3 |
||||
| B |
4 |
其实这里的分组既可以是2组,也可以是多组,分析方法都一样,为避免两组可能不足,这里举例直接分组为3组。
案例:某研究者为研究高强度间歇运动(A组)、球类运动(B组)对收缩压变化的影响,招募了15名参与者,并随机分到高强度间歇运动(A组)、球类运动(B组)、对照组(C组),两个干预组要求研究对象每天进行相应时间的运动,对照组要求干预期间不能进行有规律的运动,保持日常正常工作学习即可,并分别在基线、第3周、第7周测量血压。
具体如下:
| 分组 |
ID |
T0 |
T3 |
T7 |
| A |
1 |
130 |
125 |
124 |
| A |
2 |
120 |
119 |
117 |
| A |
3 |
140 |
130 |
120 |
| A |
4 |
110 |
110 |
90 |
| A |
5 |
100 |
100 |
99 |
| B |
1 |
135 |
130 |
125 |
| B |
2 |
115 |
115 |
114 |
| B |
3 |
140 |
130 |
120 |
| B |
4 |
100 |
100 |
98 |
| B |
5 |
125 |
124 |
120 |
| C |
1 |
130 |
129 |
130 |
| C |
2 |
110 |
110 |
110 |
| C |
3 |
140 |
139 |
152 |
| C |
4 |
110 |
115 |
108 |
| C |
5 |
124 |
122 |
123 |
/*首先写入数据*/
data duo;
DO group=1 to 3;
do id=1 to 5;
input t0 t3 t7@@;
output;
end;end;
cards;
130 125 124
120 119 117
140 130 120
110 110 90
100 100 99
135 130 125
115 115 114
140 130 120
100 100 98
125 124 120
130 129 130
110 110 110
140 139 152
110 115 108
124 122 123
;
run;
proc print;quit;
/*多组重复测量方差分析程序*/
proc glm data=duo;
class group(ref=last);
model t0 t3 t7=group /nouni;
/*model语句指定3个因变量,即 t0 t3 t7,
自变量是分组因素
nouni表示不输出单变量分析结果,因为对于重复测量分析,单变量分析意义不大*/
repeated time 3(0 3 7) contrast(1)/printe summary;
/*repeated语句指定有3个时间点,(0 3 7)表示写上时间;如果不写,默认的时间间隔是等距的,而此例是非等距的
contrast(1)表示后2个时间点分别与第1时间点比较,
printe输出球性检验,
summary输出各时间点与对照时间点的比较结果*/
manova h=group;/*给出分组变量多变量方差分析结果*/
means group/SNK;/*不同组别三个时间点分别:两两比较*/
quit;
1.下面给出了球形检验结果
本例,p=0.0416<0.05,不满足球形性要求,因此下面结果应选择多变量方差分析结果或单变量校正结果。
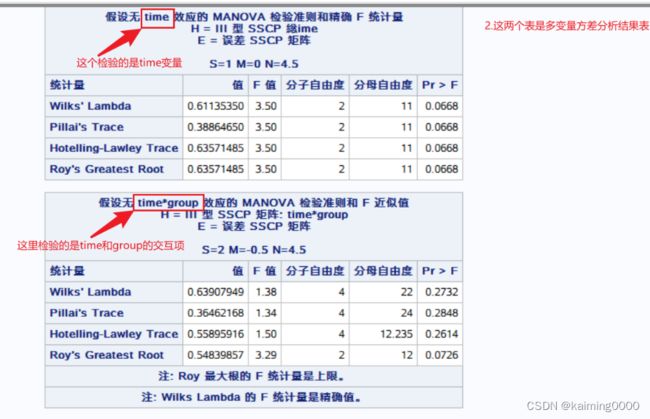
2.下面给出的是多变量方差分析结果
下面给出的是单变量方差分析结果:
结果解释:
这里发现:多变量的结果比单变量更加严格,即单变量time、group、time*group均无意义,其实按照要求,选择哪个都可以的。
下面按照单变量方差分析结果来解释:
Group:p=0.6629,说明不同组的收缩压无统计学差异
Time:p=0.0251,说明不同时间点的收缩压有统计学差异
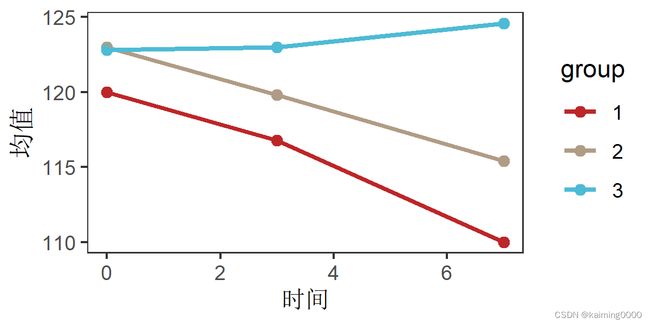
Group*Time:p=0.0919,说明不同组的变化趋势一致,无统计学差异,也就是下面三条线是平行的,可能你主观认为线条并不平行,但由于样本量太小,导致统计学检验无差异。
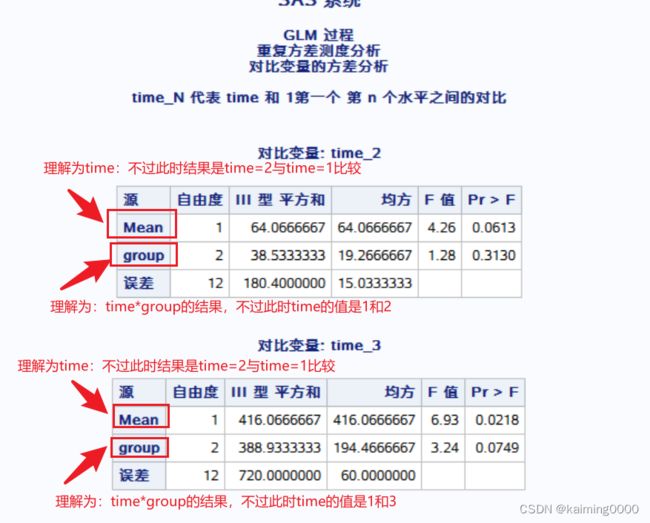
4.下面给出后两个时间点分别与对照时间点比较的结果。
对于上面表:对比变量time_2
Mean: p=0.0613,表明,时间点2与时间点1的收缩压无统计学意义。
Group:p=0.3130,表明,时间点1到时间点2三条线变化趋势一样的,也就是下面三条线平行
对于下面表:对比变量time_3
Mean: p=0.0218,表明,时间点3与时间点1的收缩压变化有统计学意义。
Group:p=0.0749,表明,时间点3到时间点2三条线变化趋势一样的,也就是下面三条线平行
5.下面三张图是t0,t3,t7三个时间点分开各组两两比较的结果。
可以看到:在t0,t3,t7三个时间点三组的收缩压均无统计学差异,这可能是样本量太少的缘故。
/*如果我们想进一步了解存在什么样的趋势,*/
/*可以通过在repeated语句中指定polynomial来实现。*/
proc glm data=duo;
class group;
model t0 t3 t7=group/nouni;
repeated time 3(0 3 7) polynomial/printe summary ;
/* polynomial来实现趋势的检验*/
quit;
首先需要说明:因为只有3个时间点,因此,只能拟合1和2次项。如果有4个时间点,则可以拟合1、2、3次项
Time_1:也就是时间的1次项,代表检验线性趋势
Mean:p=0.0233,不考虑分组,所有人收缩压随时间变化呈线性趋势
Group:p=0.0767,从线性趋势来看,三组人收缩压随时间变化趋势无明显差异
Time_2:也就是时间的2次项,代表检验曲线趋势
Mean:p=0.8405,不考虑分组,所有人收缩压随时间变化无明显曲线趋势
Group:p=0.7665,从2次项的曲线趋势来看,三组人收缩压随时间变化趋势无明显差异