计算机图形学：二维图形的几何变换（算法原理及代码实现）

一、实现方案

　　对于一个二维图形作平移、旋转、放缩变换，可以转换为在二维坐标系中图形的所有点分别可以对应到在x，y轴方向分别平移tx，ty（平移）、绕一点旋转固定的角（旋转）、在x，y轴方向分别放缩sx，sy倍。

　　对于变换的原理，只需要将原图形的点通过极坐标或者相加、相乘，再结合二维矩阵的原理即可实现，如果图形需要对图形对象进行旋转和放缩两类变换进行多次操作，则可以首先将两变换矩阵合成一个复合变换矩阵。针对于平移是矩阵的相加，为了统一成相乘，可以用齐次坐标可以解决。

　　如下为在齐次坐标下，各原点与变换矩阵形式。

　　所以，若要完成更复杂的变换，可以通过将这些基本变换合成一个复合变换，将多次运算转换成的一次性矩阵与向量相乘即可完成复杂变换。

　　如任一图形关于任意的反射轴y=a+bx的反射变换，可以转换为（1）平移-a；（2）旋转至与x/y轴重合；（3）沿x/y轴对称；（3）旋转回（2）之前的位置；（4）平移a四步即可完成。

二、代码实现

// CMatrixView 绘图
//变换矩阵
struct Matrix {
	double a[10][10];
	Matrix() {
        memset(a, 0, sizeof(a));
	}
	void init(){
		for (int i = 0; i <= 4; i++) {
				a[i][i] = 1;
		}
	}
};
//坐标点
struct Point
{
	double x, y;
};

//矩阵相乘
Matrix get_mx(Matrix a, Matrix b) {
	Matrix tmp;
	for (int i = 0; i < 3; i++) {
		for (int j = 0; j < 3; j++) {
			double sum=0;
			for (int k = 0; k < 3; k++){
				sum += a.a[i][k] * b.a[k][j];
			}
			tmp.a[i][j] = sum;
		}
	}
	return tmp;
}

//得到与矩阵相乘后的点
Point matrix_point(Point p, Matrix m) {
	Matrix n;
	n.a[0][0] = p.x;
	n.a[1][0] = p.y;
	n.a[2][0] = 1;
	for (int i = 0; i < 3; i++) {
		double sum = 0;
		for (int j = 0; j < 3; j++) {
			sum+= m.a[i][j] * n.a[j][0];
		}
		n.a[i][1] = sum;
	}
	p.x = n.a[0][1] / n.a[2][1];
	p.y = n.a[1][1] / n.a[2][1];
	return p ;
}

//平移
Matrix translate(double Tx, double Ty, Matrix m) {
	Matrix tmp;
	tmp.init();
	tmp.a[0][2] = Tx;
	tmp.a[1][2] = Ty;
	tmp = get_mx(m, tmp);
	return tmp;
}
//放缩
Matrix Shrink(double Tx, double Ty, Matrix m){
	Matrix tmp;
	tmp.init();
	tmp.a[0][0] = Tx;
	tmp.a[1][1] = Ty;
	tmp = get_mx(m, tmp);
	return tmp;
}

//旋转
Matrix revolve(double cot, Matrix m) {
	Matrix tmp;
	tmp.init();
	tmp.a[0][0] = cos(cot);
	tmp.a[1][1] = cos(cot);
	tmp.a[0][1] = -(sin(cot));
	tmp.a[1][0] = sin(cot);
	tmp = get_mx(m, tmp);
	return tmp;
}

//轴对称
Matrix axisymmetric(int x, Matrix m) {
	Matrix tmp;
	tmp.init();
	//x==1为x轴对称
	if (x == 1) {
		tmp.a[1][1] = -1;
	}
	//否则为y轴对称
	else {
		tmp.a[0][0] = -1;
	}
	tmp = get_mx(m, tmp);
	return tmp;
}

//关于任意轴对称
Matrix symmetry(double k, double b, Matrix m) {
	Matrix tmp;
	tmp.init();
	//先平移
	double cot = atan(k);
	tmp = translate(0, -b, tmp);
	//再旋转
	tmp = revolve(cot, tmp);
	//再沿x轴对称
	tmp = axisymmetric(1, tmp);
	//再旋转
	tmp = revolve(-cot, tmp);
	//再平移
	tmp = translate(0, b, tmp);
	tmp = get_mx(m, tmp);
	return tmp;
}

void Line(CDC* pDC, Point p1, Point p2) {
	pDC->MoveTo(p1.x, p1.y);
	pDC->LineTo(p2.x, p2.y);
}

void Linepoly(CDC* pDC, Point p1, Point p2,Point p3,int color) {
	CPen m_newPen, * m_oldPen;
	//创建新画笔
	m_newPen.CreatePen(PS_SOLID, 3,color);
	//将新画笔选入设备上下文，并且保存旧画笔
	m_oldPen = pDC->SelectObject(&m_newPen);
	pDC->MoveTo(p1.x, p1.y);
	pDC->LineTo(p2.x, p2.y);
	pDC->MoveTo(p2.x, p2.y);
	pDC->LineTo(p3.x, p3.y);
	pDC->MoveTo(p3.x, p3.y);
	pDC->LineTo(p1.x, p1.y);
	pDC->SelectObject(m_oldPen);

}
//实现程序：
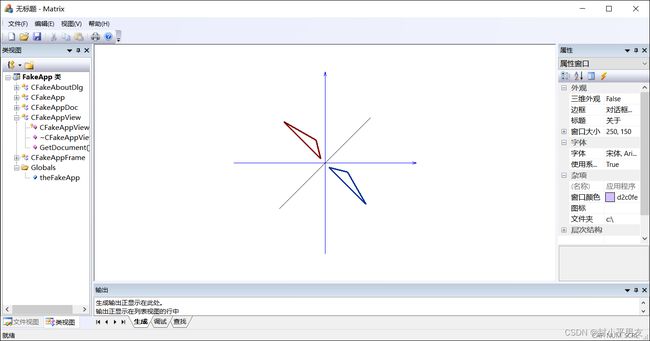
//沿任意轴对称
	Point p7 = { -10,10 };
	Point p8 = { -90,90 };
	Point p9 = { -20,50 };
	//变换前为棕红色
	Linepoly(pDC, p7, p8, p9,RGB(128,0,0));
	Point p10 = { -100,-100 };
	Point p11 = {100,100};
	Line(pDC, p10, p11);
	Matrix m4;
	m4.init();
	m4 = symmetry(1, 0, m4);
	p7 = matrix_point(p7, m4);
	p8 = matrix_point(p8, m4);
	p9 = matrix_point(p9, m4);
	//变换后为蓝色
	Linepoly(pDC, p7, p8, p9,RGB(0,51,153));

三、代码运行结果