【算法实验】算法分析与设计第二次实验Lab2

第1关：0-1背包问题

描述
需对容量为c 的背包进行装载。从n 个物品中选取装入背包的物品，每件物品i 的重量为wi ，价值为pi 。对于可行的背包装载，背包中物品的总重量不能超过背包的容量，最佳装载是指所装入的物品价值最高。

输入
多个测例，每个测例的输入占三行。第一行两个整数：n（n<=10）和c，第二行n个整数分别是w1到wn，第三行n个整数分别是p1到pn。
n 和 c 都等于零标志输入结束。

输出
每个测例的输出占一行，输出一个整数，即最佳装载的总价值。

输入样例
1 2
1
1
2 3
2 2
3 4
0 0

输出样例
1
4

#include 
using namespace std;

int n[100], c[100];
int w[100][10], p[100][10];
int maxv[100] = {0};

void dfs(int n, int c, int i, int tw, int tv, int k)
{
    if(i == n)
    {
        if(tw <= c && tv > maxv[k])
        {
            maxv[k] = tv;
        }
    }
    else
    {
        if(tw + w[k][i] <= c)
        {
            dfs(n, c, i + 1, tw + w[k][i], tv + p[k][i], k);  
        }
        
        dfs(n, c, i + 1, tw, tv, k);
    }
}

int main()
{
    int i, j;
    int count = 0;
    while(cin >> i >> j)
    {
        if(i != 0 || j != 0)
        {
            n[count] = i, c[count] = j;
            for(int k = 0; k < n[count]; k++)
            {
                cin >> w[count][k];
            }
            for(int k = 0; k < n[count]; k++)
            {
                cin >> p[count][k];
            }
            count++;
        }
        else
            break;
    }
    for(int k = 0; k < count; k++)
    {
        dfs(n[k], c[k], 0, 0, 0, k);
        cout << maxv[k] << endl;
    }
    return 0;
}

第2关：装载问题

描述
有两艘船，载重量分别是c1、 c2，n个集装箱，重量是wi (i=1…n)，且所有集装箱的总重量不超过c1+c2。确定是否有可能将所有集装箱全部装入两艘船。

输入
多个测例，每个测例的输入占两行。第一行一次是c1、c2和n（n<=10）；第二行n个整数表示wi (i=1…n)。n等于0标志输入结束。

输出
对于每个测例在单独的一行内输出Yes或No。

输入样例
7 8 2
8 7
7 9 2
8 8
0 0 0

输出样例
Yes
No

提示
求出不超过c1的最大值max，若总重量－max < c2则能装入到两艘船。

#include 
using namespace std;

int c1[100], c2[100], n[100];
int wi[100][10];
int sumw[100] = {0};
int maxw[100] = {0};

void dfs(int k, int tw, int i)
{
    if(i == n[k])
    {
        if(tw <= c1[k] && tw > maxw[k])
            maxw[k] = tw;
    }
    else
    {
        if(tw + wi[k][i] <= c1[k])
            dfs(k, tw + wi[k][i], i + 1);
        dfs(k, tw, i + 1);
    }
}

int main()
{
    int i, j, k;
    int count = 0;
    while(cin >> i >> j >> k)
    {
        if(i != 0 || j != 0 || k != 0)
        {
            c1[count] = i, c2[count] = j, n[count] = k;
            for(int m = 0; m < k; m++)
            {
                cin >> wi[count][m];
            }
            count++;
        }
        else
            break;
    }
    for(int m = 0; m < count; m++)
    {
        for(int p = 0; p < n[m]; p++)
        {
            sumw[m] += wi[m][p];
        }
    }
    for(int m = 0; m < count; m++)
    {
        dfs(m, 0, 0);
        int max2 = sumw[m] - maxw[m];
        if(max2 <= c2[m])
            cout << "Yes" << endl;
        else
            cout << "No" << endl;
    }
    return 0;
}

第3关：堡垒问题

描述
城堡是一个4×4的方格，为了保卫城堡，现需要在某些格子里修建一些堡垒。城堡中的某些格子是墙，其余格子都是空格，堡垒只能建在空格里，每个堡垒都可以向上下左右四个方向射击，如果两个堡垒在同一行或同一列，且中间没有墙相隔，则两个堡垒都会把对方打掉。问对于给定的一种状态，最多能够修建几个堡垒。

输入
每个测例以一个整数n（1<=n<=4）开始，表示城堡的大小。接下来是n行字符每行n个，‘X’表示该位置是墙，‘.’表示该位置是空格。n等于0标志输入结束。

输出
每个测例在单独的一行输出一个整数：最多修建堡垒的个数。

输入样例
4
.X…
…
XX…
…
2
XX
.X
3
.X.
X.X
.X.
3
…
.XX
.XX
4
…
…
…
…
0

输出样例
5
1
5
2
4

#include 
using namespace std;

int n;
char a[4][4];
int plan;
int maxn;

bool canplace(int m)
{
    int sx = m / n;
    int sy = m % n;
    if(a[sx][sy] == 'X')
        return false;
    for(int i = sy; i >= 0; i--)
    {
        if(a[sx][i] == '1')
            return false;
        if(a[sx][i] == 'X')
            break;
    }
    for(int i = sx; i >= 0; i--)
    {
        if(a[i][sy] == '1')
            return false;
        if(a[i][sy] == 'X')
            break;
    }
    return true;
}

void dfs(int m)
{
    if(m == n * n)
        maxn = max(plan, maxn);
    else
    {
        if(canplace(m))
        {
            a[m / n][m % n] = '1';
            plan++;
            dfs(m + 1);
            plan--;
            a[m / n][m % n] = '.';
        }
        dfs(m + 1);
    }
}

int main()
{
    int result[100] = {0};
    int count = 0;
    while((cin >> n) && n)
    {
        plan = maxn = 0;
        for(int i = 0; i < n; i++)
        {
            for(int j = 0; j < n; j++)
            {
                cin >> a[i][j];
            }
        }
        dfs(0);
        result[count] = maxn;
        count++;
    }
    for(int i = 0; i < count; i++)
    {
        cout << result[i] << endl;
    }
    return 0;
}

第4关：8皇后问题

描述
输出8皇后问题所有结果。

输入
没有输入。

输出
每个结果第一行是No n：的形式，n表示输出的是第几个结果；下面8行，每行8个字符，‘A’表示皇后，‘.’表示空格。不同的结果中，先输出第一个皇后位置靠前的结果；第一个皇后位置相同，先输出第二个皇后位置靠前的结果；依次类推。

输入样例
无输入样例

输出样例
输出的前几行：
No 1:
A…
…A…
…A
…A…
…A…
…A.
.A…
…A…
No 2:
A…
…A…
…A
…A…
…A.
…A…
.A…
…A…

提示
输出样例是正确输出结果的前几行。

#include 
#include 
using namespace std;

int q[9];
char result[9][9];
int count = 0;

void display(int n) //输出一个解
{
    cout << "No " << ++ count << ":" << endl;
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= n; j++)
        {
            if(j == q[i])
                cout << "A";
            else
                cout << result[i][j];
        }
        cout << endl;
    }
}

/**
 * 放置皇后函数
 * 
 * 如果i == 1，即第一个皇后，直接放置，返回true
 * 如果j < i，即不是第一个，则从1~i - 1开始循环，如果有一个满足同行同列同对角线，返回false
*/

bool place(int i)
{
    int j = 1;
    if(i == 1)  
        return true;
    while(j < i)   
    {
        if((q[j] == q[i]) || (abs(q[j] - q[i]) == abs(j - i))) 
            return false;
        j++;
    }
    return true;
}

/**
 * 求解n皇后问题：同行、同列、同对角线不能出现两个皇后
 * 
 * i表示当前行，也表示放置第i个皇后（即每一行有一个皇后）
 * q[i]表示当前列，每个皇后的初始位置为0
 * 
 * 首先判断 如果q[i] <= n且!place()==true，即放置不成功，则列数q[i]++
 * 如果放置成功，进入if语句：如果i == n，表示所有皇后已经放置完毕，则输出一个解
 *                         否则放置未完毕，i++且q[i] = 0，继续放置下一个皇后
 * 如果未放置成功，即此皇后的q[i] > n，没有可以放置的列，则回溯到上一个皇后重新放置
*/

void queen(int n)   
{
    int i = 1; 
    q[i] = 0;   
    while(i >= 1)
    {
        q[i]++;
        while(q[i] <= n && !place(i))
            q[i]++;
        if(q[i] <= n)
        {
            if(i == n)
                display(n);
            else
            {
                i++;
                q[i] = 0;
            }
        }
        else
            i--;
    }
}

int main()
{
    for(int i = 0; i < 9; i++)
    {
        for(int j = 0; j < 9; j++)
            result[i][j] = '.';
    }
    queen(8);
    return 0;
}

第5关：素数环问题

描述
把1到20这重新排列，使得排列后的序列A满足：
a. 任意相邻两个数之和是素数
b. 不存在满足条件a的序列B使得：A和B的前k（0 <= k <= 19）项相同且B的第k+1项比A的第k+1项小。(即按字典序排列的第一项)

输入
没有输入。

输出
输出A，两个数字之间用一个空格隔开，第一个数字前面和最后一个数字后面没有空格。

#include 
using namespace std;

int a[25];  //辅助数组，用于判断当前的数是否用过
int out = 0;

/**
 * 判断素数函数
 * 
 * 如果可以除尽则不是素数，否则是素数
*/

bool isp(int m)
{
    for(int i = 2; i < m; i++)
    {
        if(m % i == 0)
            return false;
    }
    return true;
}

/**
 * 生成素数环函数
 * 
 * 素数环第一个数置1，从2开始判断
 * 如果a[i] == 0即这个数没有被用过，并且这个数和上个数互为素数，则放入环中，进入下一次循环，否则回退，再次赋为0
 * 当cur == n且首尾互为素数时，输出素数环
*/

void dfs(int cur, int n, int A[])
{
    if(out == 0)
    {
        if(cur == n && isp(A[0] + A[n - 1]) == true)
        {
            for(int i = 0; i < n; i++)
            {
                cout << A[i] << " ";
            }
            cout << endl;
            out = 1;
        }
        else
        {
            for(int i = 2; i <= n; i++)
            {
                if(a[i] == 0 && isp(i + A[cur - 1]) == true)
                {
                    A[cur] = i;
                    a[i] = 1;
                    dfs(cur + 1, n, A);
                    a[i] = 0;
                }
            }
        }  
    }
    else
        return;

}

int main()
{
    int A[20];  //存放最终结果
    A[0] = 1;
    a[1] = 1;
    dfs(1, 20, A);

    return 0;
}

第6关：迷宫问题

描述
给一个20×20的迷宫、起点坐标和终点坐标，问从起点是否能到达终点。

输入
多个测例。输入的第一行是一个整数n，表示测例的个数。接下来是n个测例，每个测例占21行，第一行四个整数x1，y1，x2，y2是起止点的位置（坐标从零开始），（x1，y1）是起点，（x2，y2）是终点。下面20行每行20个字符，’.’表示空格；’X’表示墙。

输出
每个测例的输出占一行，输出Yes或No。

输入样例
2
0 0 19 19
…
XXXXXXXXXXXXXXXXXXXX
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
0 0 19 19
…
XXXXXXXXXXXXXXXXXXX.
…
.XXXXXXXXXXXXXXXXXXX
…
XXXXXXXXXXXXXXXXXXX.
…
.XXXXXXXXXXXXXXXXXXX
…
XXXXXXXXXXXXXXXXXXX.
…
.XXXXXXXXXXXXXXXXXXX
…
XXXXXXXXXXXXXXXXXXX.
XXXXXXXXXXXXXXXXXXX.
XXXXXXXXXXXXXXXXXXX.
XXXXXXXXXXXXXXXXXXX.
…
.XXXXXXXXXXXXXXXXXXX
…

输出样例
No
Yes

#include 
using namespace std;

//依次试探每一格的左下右上是否可以走
int H[4] = {0, 1, 0, -1};
int V[4] = {-1, 0, 1, 0};

/**
 * 判断迷宫路径函数
 * 
 * 利用for循环，判断每一格的左下右上是否可以行走，如果可以，maze置为:，进入下一个循环
 * 当走到迷宫出口时，return 1
 * 
 * 如果迷宫没有出路，return 0
*/
int DFS(int in_x, int in_y, int out_x, int out_y, char maze[20][20])
{
    if(in_x == out_x && in_y == out_y)
    {
        maze[in_x][in_y] = ':';
        return 1;
    }                                                                                                                     
    for(int i = 0; i < 4; i++)
    {
        if(in_x + H[i] >= 0 && in_y + V[i] >= 0 && in_x + H[i] < 20 && in_y + V[i] < 20 && maze[in_x + H[i]][in_y + V[i]] == '.')
        {
            maze[in_x + H[i]][in_y + V[i]] = ':';
            if(DFS(in_x + H[i], in_y + V[i], out_x, out_y, maze))
                return 1;
        }
    }  
    return 0;    
}

int main()
{
    int n;
    int in_x[10], in_y[10], out_x[10], out_y[10];
    char maze[10][20][20];

    cin >> n;
    for(int i = 0; i < n; i++)
    {
        cin >> in_x[i] >> in_y[i] >> out_x[i] >> out_y[i];
        for(int j = 0; j < 20; j++)
        {
            cin >> maze[i][j];
        }
    }
    for(int i = 0; i < n; i++)
    {
        int judge = DFS(in_x[i], in_y[i], out_x[i], out_y[i], maze[i]);
        if(judge == 1)
            cout << "Yes" << endl;
        else
            cout << "No" << endl;
    }

    return 0;
}

第7关：踩气球

描述
六一儿童节，小朋友们做踩气球游戏，气球的编号是1～100，两位小朋友各踩了一些气球，要求他们报出自己所踩气球的编号的乘积。现在需要你编一个程序来判断他们的胜负，判断的规则是这样的：如果两人都说了真话，数字大的人赢；如果两人都说了假话，数字大的人赢；如果报小数字的人说的是真话而报大数字的人说谎，则报小数字的人赢（注意：只要所报的小数字是有可能的，即认为此人说了真话）。

输入
输入为两个数字，0 0表示结束；

输出
输出为获胜的数字。

输入样例
36 62 49 343 0 0

输出样例
62 49

#include 
#include 
using namespace std;

int small, big;
int mul1, mul2;//已经当前已经踩过的气球的乘积
bool judge1, judge2;

/**
 * 判断真假话函数
 * 
 * 从100开始向前判断
 * 判断小数和大数是否能够除尽k，如果可以，mul×k，进入dfs递归，后还原（如果不还原，会导致后面j1j2再次赋予错误值）
 * 
 * 判断small和big是否有可能为真话，进行judge赋值
*/
void dfs(int k)
{
    if(k <= 1)
    {
        if(mul1 == small && mul2 == big) 
            judge1 = 1, judge2 = 1;
        else if((!judge1 || !judge2) && mul1 == small)
            judge1 = 1, judge2 = 0;
        else if(!judge1 && !judge2 && mul2 == big)
            judge1 = 0, judge2 = 1;
        return;
    }

    if(mul1 * k <= small && small % k == 0)
    {
        mul1 *= k;
        dfs(k-1);
        mul1 /= k;
    }
    if(mul2 * k <= big && big % k == 0)
    {
        mul2 *= k;
        dfs(k-1);
        mul2 /= k;
    }
    dfs(k-1);
}

int main()
{
    while(cin >> big >> small, big || small)
    {
        if(small > big) 
            swap(small, big);

        mul1 = 1, mul2 = 1;
        judge1 = 0, judge2 = 0;

        dfs(100);

        if((judge1 && judge2) || (!judge1 && !judge2))
            cout << big << endl;
        else
        {
            if(judge1)
                cout << small << endl;
            else
                cout << big << endl;
        }
    }
    return 0;   
}

第8关：字母转换

描述
通过栈交换字母顺序。给定两个字符串，要求所有的进栈和出栈序列（i表示进栈，o表示出栈），使得字符串2在求得的进出栈序列的操作下，变成字符串1。输出结果需满足字典序。例如TROT 到 TORT:
[
i i i i o o o o
i o i i o o i o
]

输入
给定两个字符串，第一个字符串是源字符串，第二个字符是目标目标字符串。

输出
所有的进栈和出栈序列,输出结果需满足字典序

输入样例
madam adamm bahama bahama long short eric rice

输出样例
[ i i i i o o o i o o i i i i o o o o i o i i o i o i o i o o i i o i o i o o i o ] [ i o i i i o o i i o o o i o i i i o o o i o i o i o i o i o i i i o o o i o i o i o i o i o i o ] [ ] [ i i o i o i o o ]

#include 
#include 
#include 
#include 
using namespace std;
#define N 100005

char a[N], b[N];
stack<char> st;
vector<char> op;
int p = 1;
int q = 1;
int len = 0;

/**
 * dfs深搜进行字母转换
 * 
 * 每一个字符都经历入栈和出栈两步，所以当n > 2 * len时输出栈内元素
 * 
 * 当p < len时，将第一个字符串中剩下的元素全部入栈
 * 全部入栈后，将栈顶元素与交换后的字符串的第一个字符进行比较，如果不对应，则栈顶出栈，比较下一个，直到找到相同字符
 * 找到相同字符后再次将剩余字符入栈，重复上述过程直到输出
 * 
 * 最后将栈和向量复原，为下一次做准备
*/
void dfs(int n)
{
    if(n > 2 * len)
    {
        for(int i = 0; i < op.size(); i++)
        {
            if(i != op.size() - 1)
                cout << op[i] << " ";
            else 
                cout << op[i];
        }
        cout << endl;
        return;
    }
    if(p <= len)
    {
        op.push_back('i');
        st.push(a[p]);
        p++;
        dfs(n+1);
        op.pop_back();
        st.pop();
        p--;
    }
    if(st.size() && st.top() == b[q])
    {
        op.push_back('o');
        char tmp = st.top();
        st.pop();
        q++;
        dfs(n+1);
        q--;
        st.push(tmp);
        op.pop_back();
    }
}

int main()
{
    while(scanf("%s%s", a+1, b+1) != EOF)   //从首地址+1开始读入
    {
        int len1 = strlen(a+1);
        int len2 = strlen(b+1);
        if(len1 != len2)
        {
            cout << "[" << endl << "]" << endl;
            continue;
        }

        len = len1;
        cout << "[" << endl;
        dfs(1);
        cout << "]" << endl;
    }
    return 0;   
}

第9关：农场灌溉问题

描述
一农场由图所示的十一种小方块组成，蓝色线条为灌溉渠。若相邻两块的灌溉渠相连则只需一口水井灌溉。

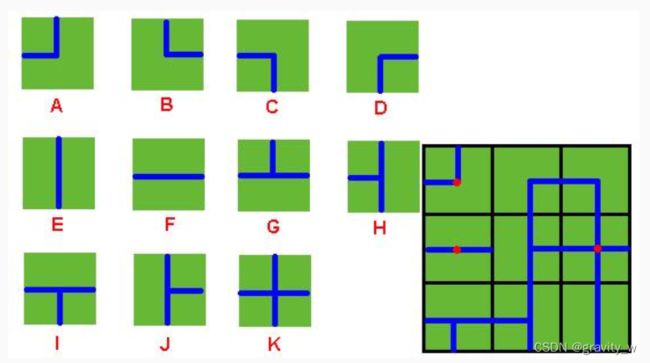
输入
给出若干由字母表示的最大不超过50×50具体由(m，n)表示，的农场图

输出
编程求出最小需要打的井数。每个测例的输出占一行。当M=N=-1时结束程序。

输入样例
2 2 DK HF 3 3 ADC FJK IHE -1 -1

输出样例
2 3

提示
参考迷宫问题，实现时关键要解决好各块的表示问题。

#include 
using namespace std;

int m, n;
char farm[100][100];
int out[128][5];
bool used[100][100];
int nextstep[4][2] = {0, -1,  -1, 0,  0, 1,  1, 0};

void init() //左上右下，有出口的赋1，对所有农场进行初始化
{
    out['A'][0] = 1, out['A'][1] = 1;

    out['B'][1] = 1, out['B'][2] = 1;

    out['C'][0] = 1, out['C'][3] = 1;

    out['D'][2] = 1, out['D'][3] = 1;

    out['E'][1] = 1, out['E'][3] = 1;

    out['F'][0] = 1, out['F'][2] = 1;

    out['G'][0] = 1, out['G'][1] = 1, out['G'][2] = 1;

    out['H'][0] = 1, out['H'][1] = 1, out['H'][3] = 1;

    out['I'][0] = 1, out['I'][2] = 1, out['I'][3] = 1;

    out['J'][1] = 1, out['J'][2] = 1, out['J'][3] = 1;

    out['K'][0] = 1, out['K'][1] = 1, out['K'][2] = 1, out['K'][3] = 1;
}

/**
 * 深搜进行灌溉渠选择
 * 
 * 将所有连通的农田分为一类，并used赋为1
 * 每一块农田均遍历左上右下，如果有一个方向是连通的，则进入搜索
*/
void dfs(int x, int y)
{
    used[x][y] = 1;
    int nx, ny;
    for(int i = 0; i < 4; i++)
    {
        nx = x + nextstep[i][0], ny = y + nextstep[i][1];
        if(nx >= 0 && nx < m && ny >= 0 && ny < n && used[nx][ny] == 0)
        {
            if(out[farm[x][y]][i] && out[farm[nx][ny]][(i + 2) % 4])
                dfs(nx, ny);
        }
    }
}

int main()
{
    init();
    while(cin >> m >> n, m != -1 || n != -1)
    {
        for(int i = 0; i < m; i++)
            for(int j = 0; j < n; j++)
                used[i][j] = 0;
        for(int i = 0; i < m; i++) 
            cin >> farm[i];

        int num = 0;
        for(int i = 0; i < m; i++)
            for(int j = 0; j < n; j++)
            {
                if(!used[i][j]) 
                {   
                    dfs(i, j);
                    num++;
                }
            }
        cout << num << endl;
    }
    return 0;
}

第10关：求图像的周长

描述
给一个用 . 和X表示的图形，图形在上、下、左、右、左上、左下、右上、右下8个方向都被看作是连通的，并且图像中间不会出现空洞，求这个图形的边长。

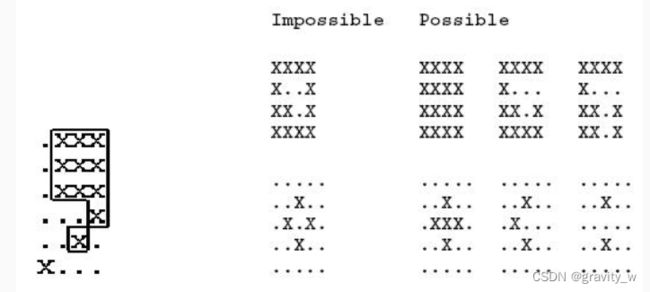
输入
首先给出m、n、x、y四个正整数，下面给出m×n的图形，x、y表示点击的位置，全0表示结束。

输出
点击的图形的周长。

输入样例
2 2 2 2 XX XX 6 4 2 3 .XXX .XXX .XXX …X …X. X… 0 0 0 0

输出样例
8 18

提示
参考迷宫问题，实现时关键要解决好各块的表示问题。

#include 
using namespace std;

int m, n, x, y;
char img[100][100];
int nextstep[8][2] = {0, -1,  -1, 0,  0, 1,  1, 0,  -1, -1,  -1, 1,  1, 1,  1, -1};
int used[100][100], cir[100][100];

/**
 * 深搜进行边长统计
 * 
 * 每个像素有八中延伸方式，判断每一种延伸方式是否符合条件
 * 如果符合条件，判断这一种延伸方式对于边长的影响
*/
void dfs(int x, int y)
{
    used[x][y] = 1;
    for(int i = 0; i < 8; i++)
    {
        int nx = x + nextstep[i][0], ny = y + nextstep[i][1];
        if(nx >= 0 && nx < m && ny >= 0 && ny < n && img[nx][ny] == 'X' && used[nx][ny] == 0)
        {
            used[nx][ny] = 1;
            int count = 0;
            for(int j = 0; j < 4; j++)
            {
                if(img[nx + nextstep[j][0]][ny + nextstep[j][1]] == 'X' && used[nx + nextstep[j][0]][ny + nextstep[j][1]] == 1)
                    count++;
            }
            if(count == 0)
                cir[nx][ny] = cir[x][y] + 4;
            else if(count == 1)
                cir[nx][ny] = cir[x][y] + 2;
            else if(count == 2)
                cir[nx][ny] = cir[x][y];
            else if(count == 3)
                cir[nx][ny] = cir[x][y] - 2;
            else
                cir[nx][ny] = cir[x][y] - 4;

            dfs(nx, ny);
        }
    }
}

int main()
{
    int num = 0;
    while(cin >> m >> n >> x >> y, m || n || x || y)
    {
        for(int i = 0; i < m; i++)
            cin >> img[i];

        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++)
                used[i][j] = 0, cir[i][j] = 0;
        }
        cir[x - 1][y - 1] = 4;
        dfs(x - 1, y - 1);
        
        int result = 0;
        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++)
            {
                result = result > cir[i][j] ? result : cir[i][j];
            }
        }
        cout << result << endl;
    }
    return 0;
}

第11关：图的m着色问题

描述
给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色，每个顶点着一种颜色。如果有一种着色法使G中每条边的2个顶点着不同颜色，则称这个图是m可着色的。图的m着色问题是对于给定图G和m种颜色，找出所有不同的着色法。

输入
第1行有3个正整数n，r 和m（n < 20,r < 200,m < 10），表示给定的图G有n个顶点和r条边，m种颜色。顶点编号为0，1，2，…，n-1。接下来的r行中，每行有2个正整数u,v，表示图G 的一条边(u,v)。

输出
输出不同的着色方案的总数。

输入样例
3 2 2
0 1
1 2

输出样例
2

#include 
using namespace std;

int n, r, m, count = 0;
int graph[200][200], color[20];

bool same(int i)
{
    for(int j = 0; j < n; j++)
    {
        if(graph[i][j] == 1 && color[i] == color[j])
            return false;
    }
    return true;
}

void dfs(int i)
{
    if(i >= n)
        count++;
    else
    {
        for(int j = 1; j <= m; j++)
        {
            color[i] = j;
            if(same(i))
                dfs(i + 1);
            color[i] = 0;
        }
    }
}

int main()
{
    cin >> n >> r >> m;
    for(int i = 0; i < r; i++)
    {
        int a, b;
        cin >> a >> b;
        graph[a][b] = 1, graph[b][a] = 1;
    }
    dfs(0);
    cout << count << endl;
    return 0;
}

第12关：三阶幻方

描述
三阶幻方是最简单的幻方，又叫九宫格，是由1,2,3,4,5,6,7,8,9九个数字组成的一个三行三列的矩阵，其对角线、横行、纵向的的和都为15。

输入
无

输出
按字典序输出所有的满足条件的幻方矩阵，每两个数字之间带一个空格，行尾无空格，每个幻方后带一个空行。

输入样例
无

输出样例
无

#include 
using namespace std;

int square[3][3], num[10];

bool judge(int x, int y, int i)
{
    if(num[i] == 1)
        return false;
    if(x == 2 || y == 2)
    {
        if(x == 2)
        {        
            if(square[0][y] + square[1][y] + square[2][y] != 15)
                return false;
            if(y == 0)
            {
                if(square[0][2] + square[1][1] + square[2][0] != 15)
                    return false;
            }
            if(y == 2)
            {
                if(square[0][0] + square[1][1] + square[2][2] != 15)
                    return false;
            }
        }
        if(y == 2)
        {
            if(square[x][0] + square[x][1] + square[x][2] != 15)
                return false;
        }
    }
    return true;
}

void dfs(int m)
{
    if(m >= 3 * 3)
    {
        for(int i = 0; i < 3; i++)
        {
            for(int j = 0; j < 3; j++)
            {
                if(j < 2)
                    cout << square[i][j] << " ";  
                else
                    cout << square[i][j];      
            }

            cout << endl;
        }
        cout << endl;
    }
    int nx = m / 3, ny = m % 3;
    for(int i = 1; i <= 9; i++)
    {
        square[nx][ny] = i;
        if(judge(nx, ny, i))
        {
            num[i] = 1;
            dfs(m + 1);
            num[i] = 0;
        }
        square[nx][ny] = 0;
    }
}

int main()
{
    dfs(0);
    return 0;
}