Learning to Learn Better Unimodal Representations via Adaptive Multimodal Meta-Learning

AMML：通过自适应多模态元学习，学会更好地学习单模态表征

总结：提出了一种 AMML 的算法，通过解耦单模态和多模态网络的学习过程，提取完全优化的单模态表征，然后将优化的单模态表征用于多模态融合。

文章信息

作者：Ya Sun；Haifeng Hu*

单位：Sun Yat-sen University（中山大学）

会议/期刊：IEEE Transactions on Affective Computing

题目：Learning to Learn Better Unimodal Representations via Adaptive Multimodal Meta-Learning

年份：2023

研究目的

• 解决以往多模态融合只能获得次优的单模态表征¹的问题。

• 缩小各模态之间的分布差异²。

研究内容

• 引入了一种基于元学习⁴的算法：自适应多模态元学习（AMML），为每种模态分配特定的元学习优化程序，从而获得每种模态的最佳的单模态表征，并将其用于多模态融合。==>解决第一个问题。
• 提出了一个分布转换层，减小模态特征分布之间的间隙，促进多模态融合。==>解决第二个问题。

研究方法

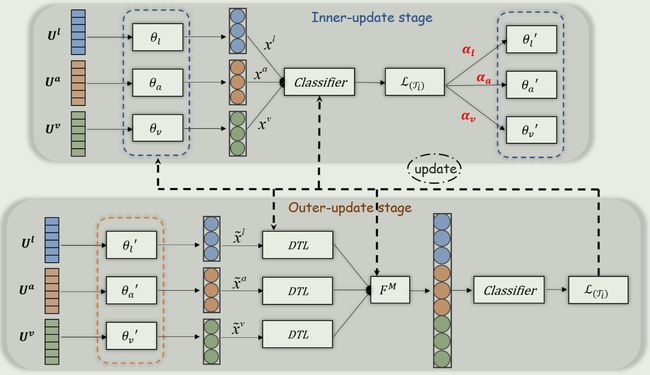
架构由三个组件组成，分别是：提取各模态有效表征的单模态子网络、缩小模态分布差距以确保融合效果的分布转换层（DTL）、生成最终推论的多模态网络。

通过自适应多模态元学习（AMML）建立这三个组件之间的联系和优化，旨在元学习特定模态的优化程序和转换层的权重，从而获得更适合多模态融合的单模态表征。

1.总体架构

融合过程：首先利用各模态的单模态子网络学习到各模态的表征，其次将其送入到 AMML 的内部更新阶段⁵，接着使用了 distribution transformation layer ⁶来调整单模态分布，然后将调整好后的三种单模态表征送入多模态网络，最后送入 AMML 的外部更新阶段⁷，实现多模态的推理。

2.网络结构

以往的多模态学习框架对所有单模态和多模态网络采用相同的优化程序。符号含义
$$\begin{array}{rl}& {\mathbf{x}}^m={\mathbf{F}}^m({\mathbf{U}}^m;{\theta }_m),m\in \{l,a,v\}\\ & y_M={\mathbf{F}}^M({\mathbf{x}}^l,{\mathbf{x}}^a,{\mathbf{x}}^v;{\theta }_M)\\ & \mathcal{L}=|y-y_M|,\theta \leftarrow \theta -\alpha \frac{\partial \ell }{\partial \theta }\end{array}$$
文中提出的新的多模态学习框架如下：符号含义

$$\begin{gathered} x^m=F^m(U^m;{\theta }_M),m\in \{l,a,v\} \\ {y}_m=C(x^m;{\theta }_C),{\mathcal{L}}^m=|y_m-y| \\ \begin{array}{rl}{\hat{\mathbf{x}}}^l,{\hat{\mathbf{x}}}^a,{\hat{\mathbf{x}}}^v,{\ell }_{diff}& =\mathbf{DTL}\end{array}({\mathbf{x}}^l,{\mathbf{x}}^a,{\mathbf{x}}^v;{\theta }_T) \\ {\mathbf{x}}^M={\mathbf{F}}^M({\hat{\mathbf{x}}}^l,{\hat{\mathbf{x}}}^a,{\hat{\mathbf{x}}}^v;{\theta }_M) \\ {y}_M=C(x^M;{\theta }_C),\mathcal{L}=|y-y_M| \end{gathered}$$

3.Unimodal Network

• language modality，使用BERT提取high-level representation。

$$\begin{array}{c}{\hat{\mathbf{X}}}^l=\mathrm{BERT}({\mathbf{U}}^l)\\ {\mathbf{X}}^l=\text{Conv}1\text{D}({\hat{\mathbf{X}}}^l,K_l)\in {\mathbb{R}}^{T_l\times d}\\ {\mathbf{x}}^l={\mathbf{X}}_{T_l}^l\in {\mathbb{R}}^d\end{array}$$

Conv1D 的作用是将输出的表征的维度转变为共享维度d，也就是为了让三种模态的维度相同。

• acoustic and visual modalities，使用transformer的encoder提取high-level representation。

$$\begin{array}{c}{\mathbf{X}}^m=\mathrm{Transformer}({\mathbf{U}}^m)\in {\mathbb{R}}^{T_m\times d},m\in \{a,v\}\\ {\mathbf{x}}^m={\mathbf{X}}_{T_m}^m\in {\mathbb{R}}^d\end{array}$$

三种模态都使用最后一个时间步的嵌入作为单模态表征来进行后续的融合。

4.Distribution Transformation Layer

• 分布转化层首先对标准正态高斯分布进行采样（意味着随机变量 $ϵ$ 是从一个均值为 0，协方差矩阵为单位矩阵 I 的多变量正态分布中抽取的。这里的单位矩阵 I 是一个每个对角线元素都是 1，其它元素都是 0 的矩阵。），

$$ϵ\sim \mathcal{N}(0,I)$$

• 然后将单模态表征的分布转化为高斯分布（利用重参数化技巧实现分布转换），

$$\begin{array}{rl}& {\mathbf{\mu }}_m,{\mathbf{\Sigma }}_m={\mathbf{\mu }}^m({\mathbf{x}}^m;{\theta }_{\mu }^m),{\mathbf{\Sigma }}^m({\mathbf{x}}^m;{\theta }_{\Sigma }^m)\\ & {\hat{\mathbf{x}}}^m={\mathbf{\mu }}_m+{\mathbf{\Sigma }}_m\times \mathbf{ϵ}\end{array}$$

​ ${\mathbf{\mu }}^m和{\Sigma }^m$ 是学习高斯分布的均值 ${\mathbf{\mu }}_m$ 和方差 ${\Sigma }_m$ 的深度神经网络。

• 最后在不同模态之间匹配转换后的分布。

---

分布转换层引入了 KL-divergence 来定量分析不同模态分布之间的差异。对三个模态中任意两个模态的 KL-divergence 求和，就得到了最终的 KL-divergence。
$${\ell }_{diff}=\sum _{m_1,m_2}{D}_{KL}(p({\hat{\mathbf{x}}}^{m_1})||q({\hat{\mathbf{x}}}^{m_2}))$$
通过最小化${\ell }_{diff}$，就可以得到通过分布转换后的最优的单模态表征${\hat{\mathbf{x}}}^m$，减少了模态之间的分布差距。

5.Multimodal Network

AMML 算法与模型无关，可以将任何序列学习网络整合到单模态网络中，也可以将任何融合方法整合到多模态网络中。因此使用了五种融合方法，验证了 AMML 的有效性。

• Direct Addition（属于非参数融合方法）

$${\mathbf{x}}^{\mathbf{M}}={\mathbf{x}}^{\mathbf{l}}+{\mathbf{x}}^{\mathbf{a}}+{\mathbf{x}}^{\mathbf{v}}$$

• Multiplication（属于非参数融合方法）

$$x^M=x^l\cdot {\mathbf{x}}^a\cdot {\mathbf{x}}^v$$

• Concatenation（AMML 的默认融合方法）

$${\mathbf{x}}^{\mathbf{M}}=FC({\mathbf{x}}^{\mathbf{l}}\oplus {\mathbf{x}}^{\mathbf{a}}\oplus {\mathbf{x}}^{\mathbf{v}})$$

​ 全连接层用于转换多模态表征的特征维度，映射特征维度到$d$.

• Tensor Fusion

  通过在单模态表征上应用外积，生成的多模态表征具有最高的表达能力，但同时也是高维和复杂的。

$$\begin{array}{rl}{\mathbf{x}}^{m^{\prime }}& =[{\mathbf{x}}^m,1],m\in \{l,v,a\}\\ {\hat{\mathbf{x}}}^{\mathbf{M}}& =FC({\otimes }_m{\mathbf{x}}^{m^{\prime }}),{\mathbf{x}}^{m^{\prime }}\in {\mathbb{R}}^{d+1}\end{array}$$

​ $\otimes$表示一套单模态向量的外积。

• Graph Fusion

  图融合将每个跨模态或特定模态的交互视为一个节点，并在节点之间进行信息传递，以模拟单模态、双模态和三模态动态。最终的图（多模态）表示是通过平均节点嵌入得到的。

6.Adaptive Multimodal Meta-Learning

AMML 解决通过单一优化程序训练的单模态网络无法同时得到优化的问题。

AMML 为每种模态分配一个特定的学习程序，其中包含两个阶段，内部更新阶段和外部更新阶段。AMML 算法的详细流程

①内部更新阶段（元训练）

在内部更新阶段，对元学习器（单模态网络）进行预训练，学习单模态表征，用分类器 C 的反向导数更新参数，获得良好的初始单模态参数。【注：元训练只在训练时使用】

内部更新阶段的loss：
$$\begin{array}{rl}& {\mathcal{L}}_{(\mathcal{T})}({\theta }_m,{\theta }_c)=\frac{1}{|\mathcal{T}|}\sum _{{\mathcal{T}}_i\in \mathcal{T}}\sum _{y\in {\mathcal{T}}_i}|y-\mathbf{C}({\mathbf{x}}^m;{\theta }_c)|\\ & {\theta }_m^{{}^{\prime }}\leftarrow {\theta }_m-{\mathbf{\alpha }}_m\circ {\nabla }_{{\theta }_m}{\mathcal{L}}_{(\mathcal{T})}({\theta }_m,{\theta }_c)\end{array}$$
②外部更新阶段（元测试）

通过多模态损失更新单模态参数，并自适应地调整每种模态的学习率和更新方向，使单模态网络适应多模态融合。（让多模态损失指导单模态网络和转换层的元更新）

外部更新阶段的loss：
L ( T ) ( θ m ′ , θ M , θ c , θ T , α m ) = 1 ∣ T ∣ ∑ T j ∈ T ∑ y ∈ T j ∣ y − C ( x M ; θ c ) ∣ + ℓ d i f f θ ← θ − β ⋅ ∇ θ L ( T ) ( θ m ′ , θ c , θ M , θ T , α m ) \begin{gathered} \mathcal{L}_{(\mathcal{T})}(\theta_m^{'},\theta_M,\theta_c,\theta_T,\boldsymbol{\alpha}_m)= \frac1{|\mathcal{T}|}\sum_{\mathcal{T}_j\in\mathcal{T}}\sum_{y\in\mathcal{T}_j}\left|y-\boldsymbol{C}(\boldsymbol{x}^M;\theta_c)\right|+\ell_{diff} \\ \theta\leftarrow\theta-\beta\cdot\nabla_\theta\mathcal{L}_{(\mathcal{T})}(\theta_m^{^{\prime}},\theta_c,\theta_M,\theta_T,\boldsymbol{\alpha}_m) \end{gathered} L(T)​(θm′​,θM​,θc​,θT​,αm​)=∣T∣1​Tj​∈T∑​y∈Tj​∑​ ​y−C(xM;θc​) ​+ℓdiff​θ←θ−β⋅∇θ​L(T)​(θm′​,θc​,θM​,θT​,αm​)​

结果与讨论

1. 通过与 SOTA 模型比较，验证了 AMML 算法的优越性。
2. 通过进行消融研究（移除可学习的${\alpha }_m$、移除MML、移除DTL、移除${\ell }_{diff}$），验证了算法中每个组件都是有效的。
3. 探讨了模型的时间与空间复杂度，表明都是可以接受的。
4. 通过使用不同的融合方法，证明了尽管融合方法简单，但是减少了模态之间的异质性，学习到更多有利于多模态融合的优化单模态表征，也是对多模态融合有帮助的。
5. 通过t-SNE算法可视化使用了DTL与未使用DTL下的单模态表征，表明了DTL是有效的。
6. 通过在是否使用元学习的两种情况下，比较单模态网络的损失，证明了在有元学习的情况下单模态表征得到了更好的优化。
7. 通过比较单模态、双模态以及三模态下的融合效果，证明了 AMML 的效果是最好的，可以有效的融合单模态信息。

代码和数据集

数据集：CMU-MOSI，CMU-MOSEI

代码：未公开

实验运行环境：GTX 1080TI（11G）

符号含义

• ${\ell }_{diff}$是最终的 KL-divergence 损失，用于测量不同模态之间的分布差异。
• ${\hat{\mathbf{x}}}^m$是分布转换后的单模态表征。
• ${\tilde{\mathbf{x}}}^m$是由 AMML 算法的外部更新阶段的单模态网络输出的单模态表征。
• ${\mathbf{\mu }}^m和{\Sigma }^m$是学习高斯分布的均值${\mathbf{\mu }}_m$和方差${\Sigma }_m$的深度神经网络。
• ${\theta }_m^{{}^{\prime }}$就是单模态网络更新后的参数。
• $\circ$表示元素乘积。
• ${\nabla }_{{\theta }_m}$表示损失函数${\mathcal{L}}_{(T)}({\theta }_m,{\theta }_c)$对${\theta }_m$的梯度。

AMML 算法

---

1. 对所有模态使用相同的优化算法，由于模态之间的异质性³，导致当多模态系统收敛时，由于不同模态的收敛行为不同，单模态网络无法完全优化（无法确保所有模态的单模态表征得到有效优化）。所以，学习到的单模态表征未达到最优化，只能获得次优的单模态表征。 ↩︎

2. distributional difference，分布差异是指不同模态之间的特征分布差异很大。 ↩︎

3. heterogeneity，异质性是指不同模态数据之间在特性、格式、分布和处理方式上的差异。 ↩︎

4. meta-learning，也被称为 learning to learn。元学习帮助机器利用先前的知识学习新任务，元学习的关键在于为各种任务开发元学习器。基于元学习的算法可以帮助机器在样本很少的情况下快速适应新任务。不过，它们主要集中在少数学习场景。 ↩︎

5. 元训练（内部更新阶段），在元训练中执行单模态任务，以获得优化的单模态表征。 ↩︎

6. 分布转换层，为了缩小不同模态之间的分布差距，调整不同模态之间的特征分布，实现更好的多模态融合。 ↩︎

7. 元测试（外部更新阶段），在元测试中执行多模态任务，通过元更新框架，以快速调整单模态网络，实现多模态推理。 ↩︎