二叉搜索树的结构:
typedef int ElemType; typedef struct SearchBiTree { ElemType Data; struct SearchBiTree *LChild,*RChild,*Parent; }SearchBiTree,*PSearchBiTree;
二叉搜索树的性质:
设 x 是二叉搜索树中的一个节点。如果 y 是 x 左子树中的一个节点,那么 y.data <= x.data。
如果 y 是 x 右子树中的一个节点,那么 y.data >= x.data。
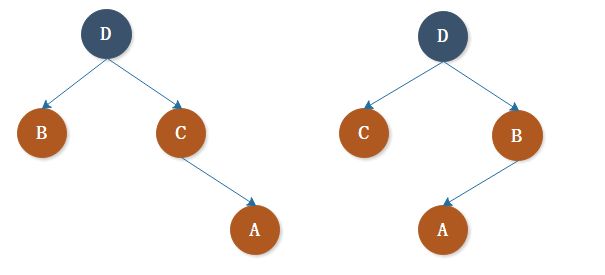
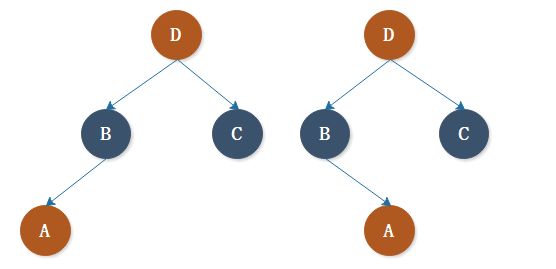
不同的二叉搜索树可以代表同一组值的集合。
插入代码:
void Tree_Insert(PSearchBiTree &T,PSearchBiTree z) { PSearchBiTree y = NULL; PSearchBiTree x = T; while(x != NULL) { y = x; if(z->Data < x->Data) x = x->LChild; else x = x->RChild; } z->Parent = y; if(y == NULL) T = z; else if(z->Data < y->Data) y->LChild = z; else y->RChild = z; }
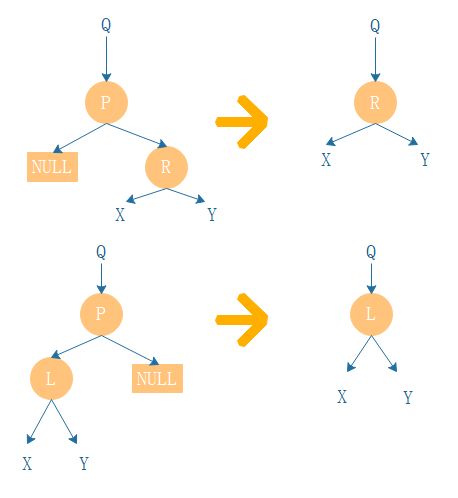
删除操作:
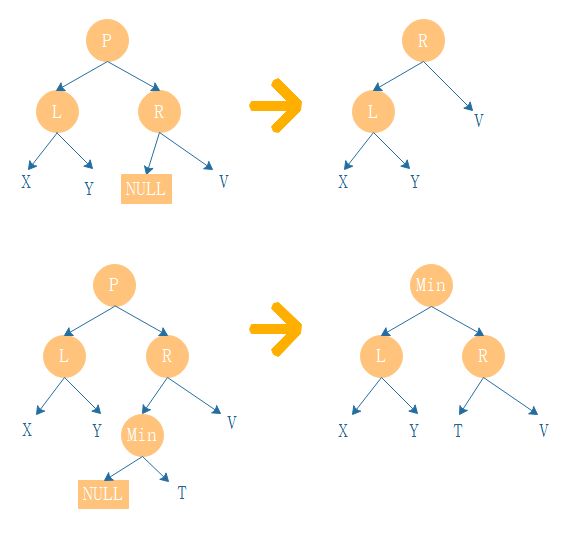
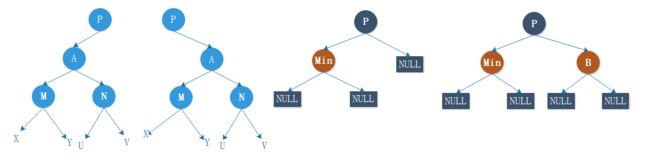
删除操作共有如下四种情况:
右下角的那种情况 Min 结点是 R子树中值最小的一个结点,所以它的左孩子为空。
删除代码:
1、替换函数:将结点 v 替换 T 树中的结点 u。
void Transplant(PSearchBiTree &T,PSearchBiTree u,PSearchBiTree v) { if(u->Parent == NULL) T = v; else if(u == u->Parent->LChild) u->Parent->LChild = v; else u->Parent->RChild = v; if(v != NULL) v->Parent = u->Parent; }
2、结点中的最小值。
PSearchBiTree Tree_Minimum(PSearchBiTree T) { while(T->LChild != NULL) T = T->LChild; return T; }
3、删除结点 z。
void Tree_Delete(PSearchBiTree &T,PSearchBiTree z) { PSearchBiTree y = NULL; if(z->LChild == NULL) Transplant(T,z,z->RChild); else if(z->RChild == NULL) Transplant(T,z,z->LChild); else { y = Tree_Minimum(z->RChild); if(y->Parent == z) { Transplant(T,y,y->RChild); y->RChild = z->RChild; y->RChild->Parent = y; } Transplant(T,z,y); y->LChild = z->LChild; y->LChild->Parent = y;
}
}
红黑树:
算法导论中树的高度似乎并不算树根。
红黑树是许多"平衡"搜索树中的一种,可以保证在最坏情况下基本动态集合操作的时间复杂度为O(lgn)。
红黑树是一颗二叉搜索树,它相对二叉搜索树增加了一个存储位来标识结点颜色,可以使 Red 或 Black。
通过对任何一条从根到叶子的简单路径上各个结点的颜色进行约束,确保没有一条路径会比其他路径长出两倍。
我们通常把带关键字的结点称为内部结点,不带关键字的结点并且其没有子结点或父结点的结点称为外部结点。
红黑树结构:
typedef enum {Red,Black}RB_Color; typedef struct RBTree { ElemType Data; struct RBTree *Left,*Right,*Parent; RB_Color Color; }RBTree,*PRBTree;
红黑性质:
1、每个结点或是红色的,或是黑色的。
2、根节点是黑色的。
3、每个叶结点是黑色的。
4、如果一个结点是红色的,则它的两个子结点都是黑色的。
5、对每一个结点,从该结点到其后代叶结点的简单路径上,均包含相同数目的黑色结点。
黑高bh:从某个结点 x 出发(不含该结点)到达一个叶结点的任意一条简单路径上的黑色结点个数,记作 bh(x)。
引理:一颗有 n 个内部结点的红黑树的高度至多为 2lg(n+1)。
推论:一颗高度为 h 的红黑树,黑高bh 至少为 (h/2)向上取整,最多为 h。
至少有 2^bh - 1 个结点,最多有 4^bh - 1个结点。
旋转操作:
如图,从右到左为左旋,从左到右为右旋。
旋转代码:
void Left_Rotate(PRBTree &T,PRBTree x) { PRBTree y = x->Right; x->Right = y->Left; if(y->Left != NULL) y->Left->Parent = x; y->Parent = x->Parent; if(x->Parent == NULL) T = y; else if(x == x->Parent->Left) x->Parent->Left = y; else x->Parent->Right = y; y->Left = x; x->Parent = y; } void Right_Rotate(PRBTree &T,PRBTree y) { PRBTree x = y->Left; y->Left = x->Right; if(x->Right != NULL) x->Right->Parent = y; x->Parent = y->Parent; if(y->Parent == NULL) T = x; else if(y == y->Parent->Left) y->Parent->Left = x; else y->Parent->Right = x; x->Right = y; y->Parent = x; }
插入操作:
在进行编写代码之前,需要分析一下所有的插入情况:
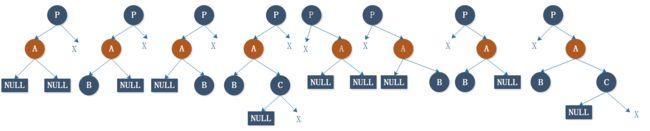
一、插入结点 A 的父结点 B 为黑色,此时插入不会破坏红黑树的性质。
二、插入结点 A 的父结点 B 为红色,且 B 结点的兄弟也为红色,
这时将不满足性质 4。但可以作相应调整:
此时,将 B 结点以及 C 结点 变成黑色,将 D 结点变成红色即可。
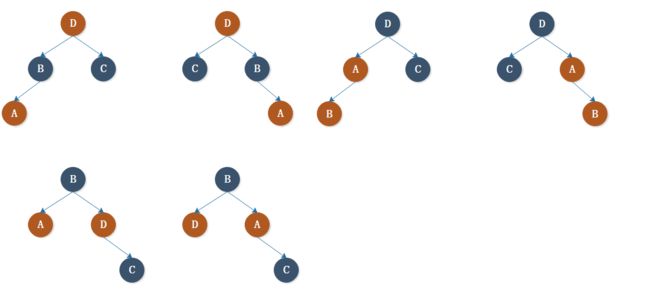
三、插入结点 A 的父结点 B 为红色,但是 B 结点的兄弟为黑色,
这是也不满足性质 4,也可以作出相应调整:
分别对以上四图变化后,对图一、图二先变色后,分别右旋 DB,左旋 DB。
而图三、图四分别左旋 BA,右旋 BA 后,就变成了图一、图二。
相关操作如下所示:
插入代码:
void RB_Insert(PRBTree &T,PRBTree z) { PRBTree y = NULL; PRBTree x = T; while(x != NULL) { y = x; if(z->Data < x->Data) x = x->Left; else x = x->Right; } z->Parent = y; if(y == NULL) T = z; else if(z->Data < y->Data) y->Left = z; else y->Right = z; z->Left = NULL; z->Right = NULL; z->Color = Red; RB_Insert_Fixup(T,z); }
插入修正代码:
void RB_Insert_Fixup(PRBTree &T,PRBTree z) { PRBTree y = NULL; while(z->Parent->Color = Red) { if(z->Parent == z->Parent->Parent->Left) { y = z->Parent->Parent->Right; if(y->Color == Red) { z->Parent->Color = Black; y->Color = Black; z->Parent->Parent->Color = Red; z = z->Parent->Parent; } else if(z = z->Parent->Right) { z = z->Parent; Left_Rotate(T,z); } z->Parent->Color = Black; z->Parent->Parent->Color = Red; Right_Rotate(T,z->Parent->Parent); } else { y = z->Parent->Parent->Left; if(y->Color = Red) { z->Parent->Color = Black; y->Color = Black; z->Parent->Parent->Color = Red; z = z->Parent->Parent; } else if(z == z->Parent->Left) { z = z->Parent; Left_Rotate(T,z); } z->Parent->Color = Black; z->Parent->Parent->Color = Red; Left_Rotate(T,z->Parent->Parent); } } T->Color = Black; }
删除操作:
与 n 个结点的红黑树上的其他的基本操作一样,删除一个结点需要花费 O(lgn) 时间。
下面给出几种删除情况:
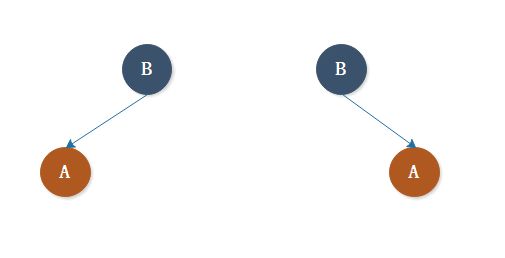
一、先给出简单的删除情况:被删除结点 A 为 红色,结点 A 的兄弟和孙子没有画出。
这几种情况可以直接将结点 A 为删除,红黑树性质不会被破坏。
删除结点 A 后情况如下图:
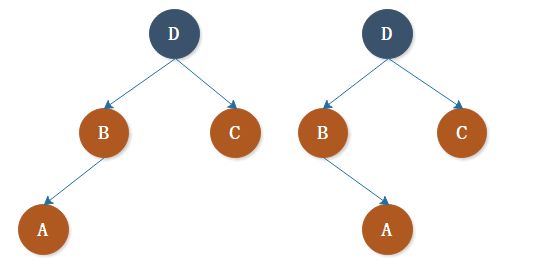
二、比较复杂的就是如下左边的这种图,因为此时会破坏红黑性质 5 或可能破坏红黑性质 4。
让我们先来分析一下,A 的父结点和子孙结点颜色不确定,用蓝色表示。
如若我们删除 A 结点,则需要寻找一个结点替代结点 A 的位置并变成结点 A 的颜色。
我们可以寻找比 A 小且相邻的结点,也就是 A 的右子树中最小的一个结点,用 Min 表示。
我们任然不知道结点 Min 的颜色,这里先分析简单的,让它以红色表示。
因为要保持红黑性质,所以有如下两种情况:
这两种情况只需要简单的将 Min 结点替换到 A 的位置并将颜色变成 A 的颜色即可。
三、任然是上面左边两个图,当结点 Min 的颜色是黑色时,情况就比较复杂了。
因为当移走黑色的结点 Min 后,会破坏红黑性质 5,可能会破坏红黑性质 4。
1、当 Min 结点的右孩子 C 为红色时的情况如下:
这种情况比较简单,只需要将 C 结点替换到 Min 结点的位置并将颜色变成黑色即可解决问题。
Min 的兄弟结点只画了一种情况,其他情况也一样,但要保持红黑性质。
2、当 Min 结点的右孩子为黑色时的情况如下:
当 Min 结点删除后,我们需要找到一个红结点填到 Min 的那个路径上,并将颜色变成黑色。
所以当 P 的颜色为红色时,我们只需要左旋一下 PB,并将 P结点颜色变成黑色即可。
但是当 P 的颜色为黑色时,我们就得在 P 的右子树中寻找一个红结点了。
因此我们把这两种情况和成一种情况,就是把 P 的颜色当作黑色讨论。
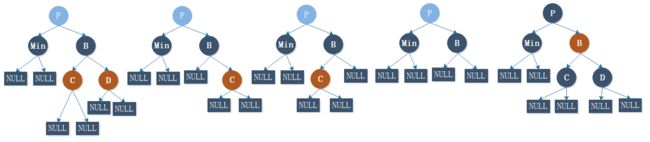
3.1、对于前三个图,我们可以归为一种情况:也就是第二个图的那种情况:
第二张图的特点是 Min 结点的兄弟的右孩子 C 为 红色:
我们先将 PB 左旋,然后颜色互换,再将 C 结点的颜色变成黑色即可。
第三个图是先将 DC 右旋,然后颜色互换,就变成了第二张图的情况。
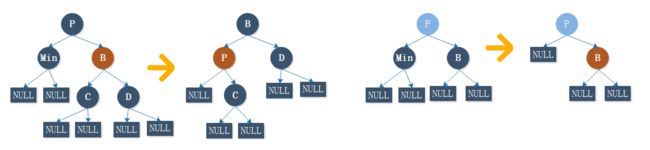
3.2、对于第五个图其实可以和第四个图同为一种情况。
我们已经无法在 P 树的内部寻找到一个合适的红色结点来替换 Min 的位置了。
所以此时我们得在 P 树的祖先中寻找一个红色结点来增加 P 树的树高。
我们将 P 结点设为新的起始点,代替原来 Min 的右结点也就是空结点。
当 P 作为新的起始点后,我们需要判断 P 结点是其父结点的左孩子还是右孩子。
如果是左孩子则执行相同的操作,否则便将该左旋的地方右旋,该右旋的地方左旋,
属性为 left 的地方变成 right,属性为 right 的地方变成 left。
总而言之,就是左右互换就对了。最后将起始点颜色变成黑色。
删除代码:
1、红黑树替换和寻找最小值:
void RB_Transplant(PRBTree &T,PRBTree u,PRBTree v) { if(u->Parent == NULL) T = v; else if(u == u->Parent->Left) u->Parent->Left = v; else u->Parent->Right = v; v->Parent = u->Parent; } PRBTree RBTree_Minimum(PRBTree T) { while(T->Left != NULL) T = T->Left; return T; }
2、红黑树删除:
void RB_Delete(PRBTree &T,PRBTree z) { PRBTree y = z; PRBTree x = NULL; RB_Color Original_Color = y->Color; if(z->Left = NULL) { x = z->Right; RB_Transplant(T,z,z->Right); } else if(z->Right == NULL) { x = z->Left; RB_Transplant(T,z,z->Left); } else { y = RBTree_Minimum(z->Right); Original_Color = y->Color; x = y->Right; if(y->Parent == z) x->Parent = y; else { RB_Transplant(T,y,y->Right); y->Right = z->Right; y->Right->Parent = y; } RB_Transplant(T,z,y); y->Left = z->Left; y->Left->Parent = y; y->Color = z->Color; } if(Original_Color == Black) RB_Delete_Fixup(T,x); }
3、红黑树修正:
void RB_Delete_Fixup(PRBTree &T,PRBTree x) { PRBTree w = NULL; while(x != T && x->Color == Black) { if(x == x->Parent->Left) { w = x->Parent->Right; if(w->Color == Red) { w->Color = Black; x->Parent->Color = Red; Left_Rotate(T,x->Parent); w = x->Parent->Right; } if(w->Left->Color == Black && w->Right->Color == Black) { w->Color = Red; x = x->Parent; } else { if(w->Right->Color == Black) { w->Left->Color = Black; w->Color = Red; Right_Rotate(T,w); w = x->Parent->Right; } w->Color = x->Parent->Color; x->Parent->Color = Black; w->Right->Color = Black; Left_Rotate(T,x->Parent); x = T; } } else { w = x->Parent->Left; if(w->Color == Red) { w->Color = Black; x->Parent->Color = Red; Right_Rotate(T,x->Parent); w = x->Parent->Left; } if(w->Right->Color == Black && w->Left->Color == Black) { w->Color = Red; x = x->Parent; } else { if(w->Left->Color == Black) { w->Right->Color = Black; w->Color = Red; Left_Rotate(T,w); w = x->Parent->Left; } w->Color = x->Parent->Color; x->Parent->Color = Black; w->Left->Color = Black; Right_Rotate(T,x->Parent); x = T; } } } x->Color = Black; }
若有错误请多担待,谢谢!