数据结构+算法(第14篇):精通二叉树的“独门忍术”——线索二叉树(中)
作者简介:大家好,我是smart哥,前中兴通讯、美团架构师,现某互联网公司CTO
联系qq:184480602,加我进群,大家一起学习,一起进步,一起对抗互联网寒冬
学习必须往深处挖,挖的越深,基础越扎实!
阶段1、深入多线程
阶段2、深入多线程设计模式
阶段3、深入juc源码解析
阶段4、深入jdk其余源码解析
阶段5、深入jvm源码解析
码哥源码部分
码哥讲源码-原理源码篇【2024年最新大厂关于线程池使用的场景题】
码哥讲源码【炸雷啦!炸雷啦!黄光头他终于跑路啦!】
码哥讲源码-【jvm课程前置知识及c/c++调试环境搭建】
码哥讲源码-原理源码篇【揭秘join方法的唤醒本质上决定于jvm的底层析构函数】
码哥源码-原理源码篇【Doug Lea为什么要将成员变量赋值给局部变量后再操作?】
码哥讲源码【你水不是你的错,但是你胡说八道就是你不对了!】
码哥讲源码【谁再说Spring不支持多线程事务,你给我抽他!】
终结B站没人能讲清楚红黑树的历史,不服等你来踢馆!
打脸系列【020-3小时讲解MESI协议和volatile之间的关系,那些将x86下的验证结果当作最终结果的水货们请闭嘴】
引言
上一篇文章《精通二叉树的“独门忍术”——线索二叉树(上)》提到了线索二叉树的改良,并给出了改良后的“中序遍历”“前序遍历”线索二叉树的定义。本文就来谈谈改良后的“前序遍历”的线索二叉树的转换与遍历算法。
非递归型算法
既然《精通二叉树的“独门忍术”——线索二叉树(上)》中已经给出了“中序遍历”的线索二叉树的转换与遍历算法,那么朴素的想法就是:将“前序遍历”线索二叉树与“中序遍历”线索二叉树进行对比,基于后者来推导出前者的算法。
我们先来对比一下“中序遍历”线索二叉树与“前序遍历”线索二叉树的图示:
图1 “中序遍历”的线索二叉树
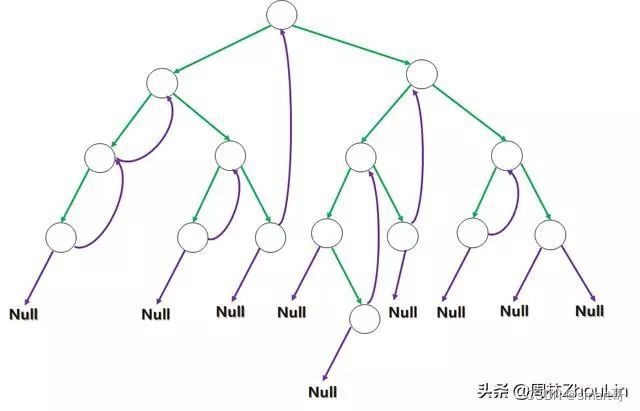
图2 “前序遍历”的线索二叉树
对比图2与图1可以看出:
“中序遍历”线索二叉树与“前序遍历”线索二叉树的区别仅仅在于后继节点的位置——前者是当前节点,后者是当前节点的直接右孩子。
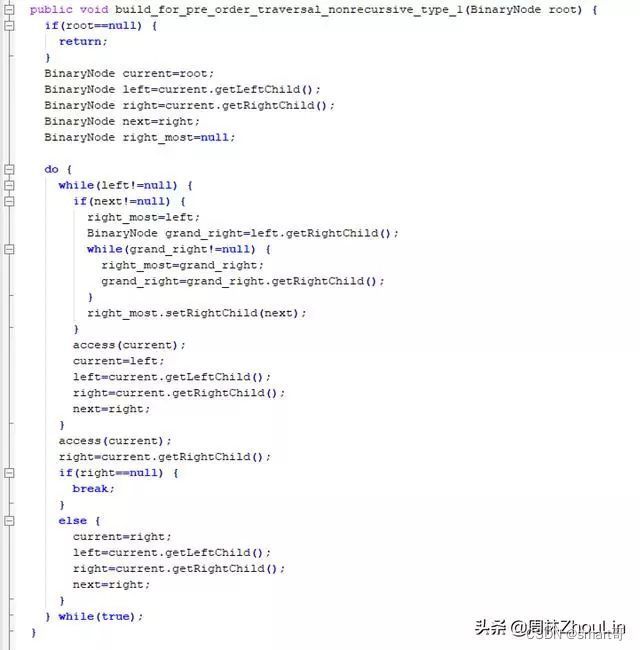
因此,我们可以完全照搬“中序遍历”线索二叉树的算法,仅仅将后继节点的代码改一下即可:
递归型算法
还有别的方法吗?
我们来看看是否可以利用传统线索二叉树——即“中序遍历”的线索二叉树,来实现这一目标:非递归地、不用堆栈来做“前序遍历”。
前序遍历的规则简单归纳就是:递归执行“根”->“左”->“右”。
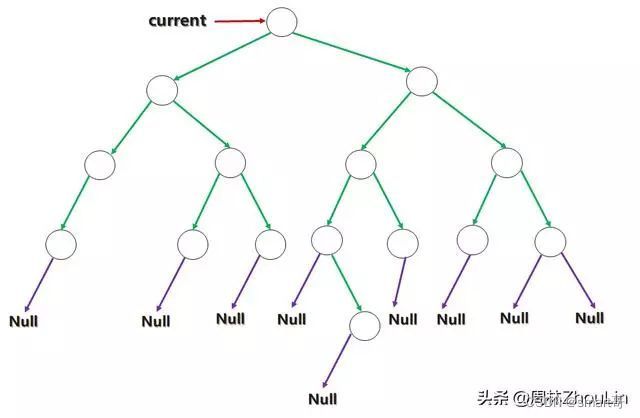
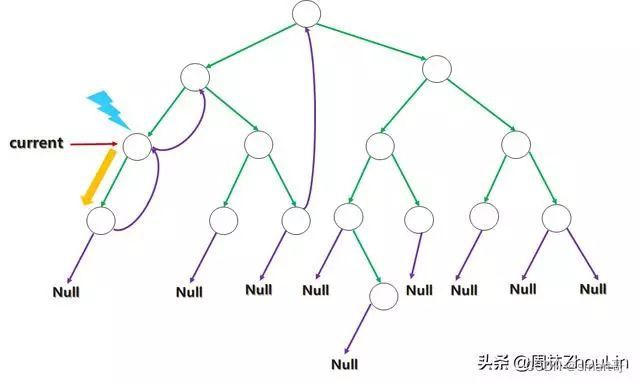
下面的几张图表示了从树根开始“前序遍历”一部分左子树的过程。其中current指针表示当前位置,蓝色闪电表示该位置进行遍历输出,橙黄色箭头表示current指针移动方向。
先将当前节点的前驱节点找到,链接起来便形成“中序遍历”的线索二叉树;同时,当前节点是当前局部线索二叉树的树根,根据“根”->“左”->“右”的前序遍历规则,应该输出当前位置作为“根”信息。
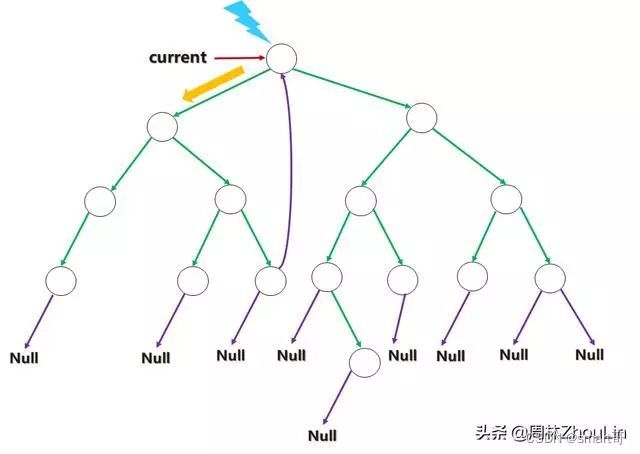
将当前节点位置指针向左孩子移动。
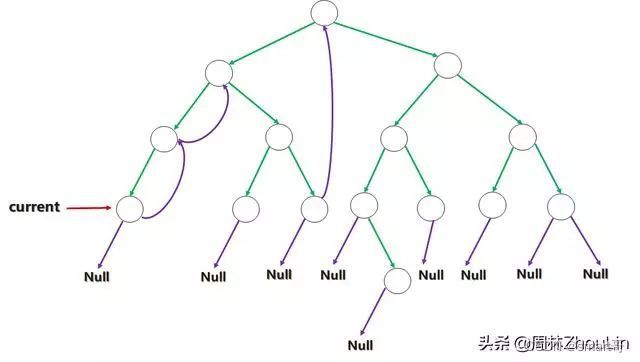
当前位置指针移动到叶子节点时(这种场景的“特征识别码”是:其左孩子指针指向空节点),输出当前位置之后,向当前节点的右孩子指针方向移动。
一边移动,一边将之前添加的“前驱->后继”的线索去掉,以便还原成原始二叉树。
这种场景的“特征识别码”是:当前节点是前驱节点的右孩子。
根据上面的分析,很容易翻译成如下的基于“中序遍历”的线索二叉树、非递归型、不用堆栈、并且遍历完后还可以恢复成原始二叉树的“神算法”:
后记
研究算法,和研究数学问题一样,“一题多解”可以极大拓宽思路和增强想象力、“防止老年痴呆”哦:)
老规矩,留个思考题、答案在下一篇文章揭晓:
最后的这个“神算法”的时间复杂度是多少呢?