图论练习题
图论练习题
-
- 1.把{1,2,3,4,5}任划分成两个子集。则必有一个子集含有两数及其差。
- 2.在2n(n≥2)个人组成的人群中,每人至少有n个朋友.则存在四阶圈.
- 3. k维立方体:以分量为0或1的k维向量集为顶集, 仅当两向量只有一个同位分量相异时,相应的两顶相邻. ( k ∈ N k\in N k∈N)证:k维立方体是顶数 2 k , 2^k, 2k,边数 k 2 k − 1 k2^{k-1} k2k−1的二分图.
- 4. 证明: 无环图G必定存在二分生成子图H, 使得 ∀ v ∈ V ( G ) \forall v \in V(G) ∀v∈V(G), 都有 d H ( v ) ≥ 1 2 d G ( v ) d_H(v)\ge \frac12d_G(v) dH(v)≥21dG(v)
- 5.若G是连通图, 每顶皆偶次, 则 ∀ v ∈ V ( G ) , \forall v\in V(G), ∀v∈V(G),都有 ω ( G − v ) ≤ 1 2 d ( v ) \omega(G-v)\le \frac12d(v) ω(G−v)≤21d(v)
- 6.若G是单图, δ ≥ 2 \delta\ge2 δ≥2,则G中至少有长为 δ + 1 \delta+1 δ+1的圈.
- 7.图G是林,且有2k个奇次顶. 则G中有k条无公共边的轨, 使得G的每条边都在这些轨上.
- 8.若 d 1 , d 2 , . . . , d v d_1,d_2,...,d_v d1,d2,...,dv是正整数序列,且 Σ i = 1 v d i = 2 ( v − 1 ) \Sigma_{i=1}^{v}d_i=2(v-1) Σi=1vdi=2(v−1),则此序列是树的次数序列.
- 9.在至少三个顶的连通图G中,至少有两个顶,从G中把这两个顶删除后所得之子图仍连通.
- 10.若T是顶数不小于3的树, T的直径是2, 则T是星.
- 11.S={ x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn}是平面上的点组成的集合. n ≥ 3 , n\ge3, n≥3,S中任二点的距离至少为1. 证明距离恰为1的顶对最多有3n-6对.
- 12.若平面图G的顶数不小于11,则 G c G^c Gc不是平面图
- 13.树上是否可能有两个不同的完备匹配?
- 14.设G是k次正则连通图,顶数是偶数,至少删除不少于k-1条边,才可能使G的连通片数增多,试证G中有完备匹配.
- 15.证明树有完备匹配的充要条件是 ∀ v ∈ V ( G ) , o ( G − v ) = 1. \forall v\in V(G), o(G-v)=1. ∀v∈V(G),o(G−v)=1.
- 16.对二分图进行 δ \delta δ边着色,能使得每顶所关联的边中皆出现 δ \delta δ种颜色.
- 17.G是奇数个顶的k次正则图(k>0),则 χ ′ ( G ) = Δ + 1 \chi'(G)=\Delta+1 χ′(G)=Δ+1
- 18.若G中任二奇圈皆有公共顶点,则 χ ( G ) ≤ 5. \chi(G)\le5. χ(G)≤5.
- 19.对G的任意子图H都有 α ( H ) ≥ ∣ V ( H ) ∣ 2 , \alpha(H)\ge\frac{|V(H)|}{2}, α(H)≥2∣V(H)∣,则G是二分图.
- 20.顶数2k-1的k次正则图G是Hamilton图( k ≥ 2 k\ge2 k≥2)
- 21.若 u , v ∈ V ( G ) u,v\in V(G) u,v∈V(G), u , v u,v u,v不相邻,且 d ( v ) + d ( u ) ≥ ∣ V ( G ) ∣ d(v)+d(u)\ge |V(G)| d(v)+d(u)≥∣V(G)∣,且 G + u v G+uv G+uv是 H a m i l t o n Hamilton Hamilton图,证 G G G也是 H a m i l t o n Hamilton Hamilton图.
1.把{1,2,3,4,5}任划分成两个子集。则必有一个子集含有两数及其差。
①将{1,2,3,4,5}任划分成两个子集标注为 S 1 , S 2 S_1,S_2 S1,S2;
②以{1,2,3,4,5,6}为顶集,构造 K 6 K_6 K6,让 S 1 , S 2 S_1,S_2 S1,S2对应颜色1,2.
③对 u , v ∈ K 6 u,v\in K_6 u,v∈K6,当且仅当 ∣ u − v ∣ ∈ S i , e u v |u-v|\in S_i ,e_{uv} ∣u−v∣∈Si,euv染i色. i ∈ { 1 , 2 } i\in\{1,2\} i∈{1,2}
④当存在三角形 Δ u v w \Delta uvw Δuvw三边同色时, 不妨设 x = u − v > 0 , y = v − w > 0 , 则 z = u − w > 0 x=u-v>0,y=v-w>0,则z=u-w>0 x=u−v>0,y=v−w>0,则z=u−w>0. x , y , z 同属于一个子集 S i ( i ∈ { 1 , 2 } ) x,y,z同属于一个子集S_i(i\in\{1,2\}) x,y,z同属于一个子集Si(i∈{1,2}),且 x = z − y x=z-y x=z−y, 子集 S i S_i Si含有两数及其差.
⑤(拉姆齐数Ramsey) 由r(3,3)=6, 可证明 Δ u v w \Delta uvw Δuvw的存在性.
2.在2n(n≥2)个人组成的人群中,每人至少有n个朋友.则存在四阶圈.
①以人为顶,当且仅当顶点互为朋友时顶点相邻.得到2n个顶的图G.
②假设图G所有顶对都互相相邻,则显然存在四阶圈.
③若存在不相邻的顶对{u,v},根据已知条件,有 d ( u ) ≥ n , d ( v ) ≥ n d(u)\ge n,d(v)\ge n d(u)≥n,d(v)≥n,又剩余顶数为 2 n − 2 2n-2 2n−2,故 u , v u,v u,v至少存在两个公共邻居 x , y x,y x,y. 则存在四阶圈 u x v y uxvy uxvy.
3. k维立方体:以分量为0或1的k维向量集为顶集, 仅当两向量只有一个同位分量相异时,相应的两顶相邻. ( k ∈ N k\in N k∈N)证:k维立方体是顶数 2 k , 2^k, 2k,边数 k 2 k − 1 k2^{k-1} k2k−1的二分图.
k维立方体的顶与k维向量组为1对1的映射.
①顶数?
k维向量组的向量总个数为 2 k 2^k 2k,也即顶数.
②边数?
对k维向量. 当固定k-1个坐标后, 剩下一个坐标或为1或为0,对应两个相邻顶, 也即对应一条边. 所以总边数有 ε = C k k − 1 2 k − 1 = k 2 k − 1 \varepsilon=C_{k}^{k-1}2^{k-1}=k2^{k-1} ε=Ckk−12k−1=k2k−1.
③二分图?
按每个顶坐标和的奇偶性, 把顶划分为两个子集. 则在同个子集的顶具有相同的奇偶性, 故互不相邻, 满足二分图的性质.
4. 证明: 无环图G必定存在二分生成子图H, 使得 ∀ v ∈ V ( G ) \forall v \in V(G) ∀v∈V(G), 都有 d H ( v ) ≥ 1 2 d G ( v ) d_H(v)\ge \frac12d_G(v) dH(v)≥21dG(v)
(存在性题目, H的边数越多, 则不等式成立的可能性越大)
①令H是G的边数最大的二分生成子图. 且 H H H被划分为 X X X和 Y Y Y.
②假设 ∃ v ∈ X \exist v\in X ∃v∈X, 满足 d H ( v ) < 1 2 d G ( v ) d_H(v)<\frac12d_G(v) dH(v)<21dG(v).
③将在图G中与 v v v关联的边集划分为 E 1 , E 2 E_1, E_2 E1,E2,其中 E 1 E_1 E1表示边的另一端在 X X X中的边, E 2 E_2 E2表示边的另一端在 Y Y Y中的边.
则 d H ( v ) = ∣ E 1 ∣ , d G ( v ) = ∣ E 1 ∣ + ∣ E 2 ∣ , 由②中假设推 , ∣ E 1 ∣ ≥ ∣ E 2 ∣ . d_H(v)=|E_1|,d_G(v)=|E_1|+|E_2|, 由②中假设推, |E_1|\ge |E_2|. dH(v)=∣E1∣,dG(v)=∣E1∣+∣E2∣,由②中假设推,∣E1∣≥∣E2∣.
④ H ′ = G − ∣ E 1 ∣ + ∣ E 2 ∣ H'=G-|E_1|+|E_2| H′=G−∣E1∣+∣E2∣也是二分图,且 ε ( H ′ ) ≥ ε ( H ) , \varepsilon(H')\ge\varepsilon(H), ε(H′)≥ε(H),与①中假设矛盾.故而命题成立.
5.若G是连通图, 每顶皆偶次, 则 ∀ v ∈ V ( G ) , \forall v\in V(G), ∀v∈V(G),都有 ω ( G − v ) ≤ 1 2 d ( v ) \omega(G-v)\le \frac12d(v) ω(G−v)≤21d(v)
①设 G − v G-v G−v的全部连通片为 G 1 , G 2 , . . . , G ω , G_1,G_2,...,G_{\omega}, G1,G2,...,Gω,v与每个连通片都有边存在.
②令 m i m_i mi是 v 与 G i v与G_i v与Gi的边数( m i > 0 m_i>0 mi>0). ω ( G − v ) 简写成 ω . \omega(G-v)简写成\omega. ω(G−v)简写成ω.
{ m i = Σ u ∈ V ( G i ) d ( u ) − 2 ∣ E ( G i ) ∣ 故 m i 是大于 0 的偶数 , 即 m i ≥ 2. 又 d ( v ) = Σ i = 1 i = ω m i , 故 d ( v ) ≥ 2 ω \begin{cases}m_i=\Sigma_{u\in V(G_i)}d(u)-2|E(G_i)|&故m_i是大于0的偶数, 即m_i\ge2.\\又d(v)=\Sigma_{i=1}^{i=\omega}m_i, &故d(v)\ge2\omega\end{cases} {mi=Σu∈V(Gi)d(u)−2∣E(Gi)∣又d(v)=Σi=1i=ωmi,故mi是大于0的偶数,即mi≥2.故d(v)≥2ω
6.若G是单图, δ ≥ 2 \delta\ge2 δ≥2,则G中至少有长为 δ + 1 \delta+1 δ+1的圈.
①设 P = v 0 v 1 . . . v l P=v_0v_1...v_l P=v0v1...vl是最长轨, 则 v 0 v_0 v0的邻顶集是 v 1 , v 2 , . . . , v l {v_1,v_2,...,v_l} v1,v2,...,vl的子集.
②因 d ( v 0 ) ≥ δ d(v_0)\ge\delta d(v0)≥δ, 故 ∃ k ≥ δ , \exist k\ge \delta, ∃k≥δ, 使得 v 0 与 v k v_0与v_k v0与vk相邻
③得到圈 C = v 0 v 1 . . . v k v 0 C=v_0v_1...v_kv_0 C=v0v1...vkv0,圈C的长度 = k + 1 ≥ δ + 1 =k+1\ge\delta+1 =k+1≥δ+1
7.图G是林,且有2k个奇次顶. 则G中有k条无公共边的轨, 使得G的每条边都在这些轨上.
(归纳法)
①当k=1时,林G中有2个奇次顶. 易知G的最长轨P的起止顶为叶.则除了最长轨的起止顶外,G中其它顶的次数皆为偶数. 易证G中所有顶皆在P上.G中每条边都在P上.则k=1时命题成立.
②假设 k = k 0 ( k 0 ≥ 1 ) k = k_0(k_0\ge1) k=k0(k0≥1)时成立,图G是林,有2k个奇次项,则G中有k条无公共边的轨,使得G的每条边都在这些轨上.
③对于 k = k 0 + 1 k=k_0+1 k=k0+1时,图G存在起止顶皆为叶的轨P, 图G’=G-P有2k-2个奇次顶,偶次顶数与G相同.由归纳假设,G’中有(k-1)条无公共边的轨 P 1 , P 2 , . . . , P k − 1 P_1,P_2,...,P_{k-1} P1,P2,...,Pk−1使得G’的每条边都在这些轨上.
④则G中有k条无公共边的轨 P , P 1 , P 2 , . . . P k − 1 P,P_1,P_2,...P_{k-1} P,P1,P2,...Pk−1,使得G的每条边都在这些轨上.
8.若 d 1 , d 2 , . . . , d v d_1,d_2,...,d_v d1,d2,...,dv是正整数序列,且 Σ i = 1 v d i = 2 ( v − 1 ) \Sigma_{i=1}^{v}d_i=2(v-1) Σi=1vdi=2(v−1),则此序列是树的次数序列.
(归纳法)
①当 v = 2 v=2 v=2,必有 d 1 = 1 , d 2 = 1 d_1=1,d_2=1 d1=1,d2=1,显然是树的次数序列;
②假设当 v = k ( k ≥ 2 ) , v= k(k\ge 2), v=k(k≥2),若 Σ i = 1 k d i = 2 ( k − 1 ) \Sigma_{i=1}^{k}d_i=2(k-1) Σi=1kdi=2(k−1),则是树的次数序列.
③对于 v = k + 1 v=k+1 v=k+1,由 Σ i = 1 k + 1 d i = 2 k 且 d i > 0 → 在 d 1 , d 2 , . . . , d k + 1 中 \Sigma_{i=1}^{k+1}d_i=2k且d_i>0\to 在d_1,d_2,...,d_{k+1}中 Σi=1k+1di=2k且di>0→在d1,d2,...,dk+1中存在某个点的次数大于1,存在某个点的次数等于1.
④不妨令 d k > 1 , d k + 1 = 1 d_k>1,d_{k+1}=1 dk>1,dk+1=1.则由归纳假设可知,序列 d 1 , d 2 , . . . , d k − 1 , d k − 1 d_1,d_2,...,d_{k-1},d_k-1 d1,d2,...,dk−1,dk−1是树的次数序列.
⑤即存在一棵树T, d ( v 1 ) = d 1 , d ( v 2 ) = d 2 , . . . , d ( v k ) = d k , d(v_1)=d_1,d(v_2)=d_2,...,d(v_k)=d_k, d(v1)=d1,d(v2)=d2,...,d(vk)=dk,此时在T上新增一个顶 v k + 1 , v_{k+1}, vk+1,且令 v k , v k + 1 v_k,v_{k+1} vk,vk+1之间连一条边,得到新的树T",且树T"的序列是 d 1 , d 2 , . . . , d k + 1 d_1,d_2,...,d_{k+1} d1,d2,...,dk+1.
⑥综上可知,命题成立.
9.在至少三个顶的连通图G中,至少有两个顶,从G中把这两个顶删除后所得之子图仍连通.
(如果其生成子图都能满足连通性,那么原图更是不用说)
①设H是G的生成树. V ( H ) = V ( G ) ≥ 3 V(H)=V(G)\ge 3 V(H)=V(G)≥3,则H中至少存在两个叶子u和v,将这两个叶子从图中删除得到的子图仍然连通.H-u-v是连通图,而H-u-v是G-u-v的生成子图,故G-u-v也是连通图,证毕.
10.若T是顶数不小于3的树, T的直径是2, 则T是星.
①假设T不是星, 则T中存在两个顶 u , v u,v u,v 满足 d ( u ) > 1 , d ( v ) > 1. d(u)>1,d(v)>1. d(u)>1,d(v)>1.
② 从 u 到 v 从u到v 从u到v存在唯一的轨 P ( u , v ) P(u,v) P(u,v), 由 d ( u 0 ) > 1 知 u 由d(u_0)>1知u 由d(u0)>1知u至少有一个不在轨 P ( u , v ) P(u,v) P(u,v)上的邻点 u 0 u_0 u0,同理, v v v至少有一个不在轨 P ( u , v ) P(u,v) P(u,v)上的邻点 v 0 v_0 v0,则存在路径 u 0 P ( u , v ) v 0 , d ( u 0 , v 0 ) ≥ 3 u_0P(u,v)v_0,d(u_0,v_0)\ge3 u0P(u,v)v0,d(u0,v0)≥3,与已知条件矛盾.
故①不成立, 即T是星.
11.S={ x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn}是平面上的点组成的集合. n ≥ 3 , n\ge3, n≥3,S中任二点的距离至少为1. 证明距离恰为1的顶对最多有3n-6对.
①以S为顶集, 仅当两点距离恰为1时, 两点之间连一条边.构成图G.
②证明在图G中,不会出现有边交叉的情况. 如图,若出现交叉边,则由三角不等式知 o u + o y > u y , o y + o v > y v , . . . → u y + y v + x v + x u < 2 ( u v + x y ) = 4 ou+oy>uy,oy+ov>yv,...\to uy+yv+xv+xu<2(uv+xy)=4 ou+oy>uy,oy+ov>yv,...→uy+yv+xv+xu<2(uv+xy)=4,则在 u y , y v , x v , x u uy,yv,xv,xu uy,yv,xv,xu中存在距离小于1的顶对, 与已知条件矛盾. 故不存在线段交叉的情况.
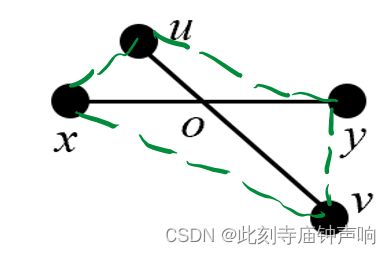
③故图G是平面图. 故有 { Σ i = 1 ϕ d ( f i ) = 2 ε 2 ε ≥ 3 ϕ 3 ϕ = 3 ( ε − n + 2 ) → ε ≤ 3 n − 6 \begin{cases}\Sigma_{i=1}^{\phi}d(f_i)=2\varepsilon\\2\varepsilon\ge3\phi\\3\phi=3(\varepsilon -n+2)\end{cases}\to \varepsilon\le3n-6 ⎩ ⎨ ⎧Σi=1ϕd(fi)=2ε2ε≥3ϕ3ϕ=3(ε−n+2)→ε≤3n−6
12.若平面图G的顶数不小于11,则 G c G^c Gc不是平面图
① { ε ( G ) ≤ 3 v − 6 ε ( G c ) + ε ( G ) = v ( v − 1 ) 2 → ε ( G c ) ≥ v ( v − 1 ) 2 − ( 3 v − 6 ) \begin{cases}\varepsilon (G)\le 3v-6\\\varepsilon(G^c)+\varepsilon(G)=\frac{v(v-1)}{2}\end{cases}\to\varepsilon(G^c)\ge\frac{v(v-1)}{2}-(3v-6) {ε(G)≤3v−6ε(Gc)+ε(G)=2v(v−1)→ε(Gc)≥2v(v−1)−(3v−6)
ε ( G c ) ≥ v ( v − 1 ) 2 − 2 ( 3 v − 6 ) + ( 3 v − 6 ) ≥ ( ν − 11 ) ( ν − 2 ) / 2 + 1 + ( 3 ν − 6 ) \begin{aligned} \varepsilon(G^c)& \ge\frac{v(v-1)}{2}-2(3v-6)+(3v-6)\\ &\ge (ν-11)(ν-2)/2+1+(3ν-6)\end{aligned} ε(Gc)≥2v(v−1)−2(3v−6)+(3v−6)≥(ν−11)(ν−2)/2+1+(3ν−6)
因为 v ≥ 11 , v\ge11, v≥11,故 ε ( G c ) > 3 v − 6 \varepsilon(G^c)>3v-6 ε(Gc)>3v−6,即 G c 不是平面图 G^c不是平面图 Gc不是平面图
13.树上是否可能有两个不同的完备匹配?
①若有两个不同的完备匹配,不妨设为 M 1 , M 2 M_1,M_2 M1,M2,则 M 1 ⊕ M 2 ≠ ϕ M_1\oplus M_2\ne\phi M1⊕M2=ϕ
② G ( M 1 ⊕ M 2 ) 中 , G(M_1\oplus M_2)中, G(M1⊕M2)中,每个顶点都是偶次 → \to →存在圈, 与树上无圈矛盾.
故假设①不成立
14.设G是k次正则连通图,顶数是偶数,至少删除不少于k-1条边,才可能使G的连通片数增多,试证G中有完备匹配.
围绕 ∀ S ⊂ G , o ( G − S ) ≤ ∣ S ∣ 展开 \forall S\subset G, o(G-S)\le|S|展开 ∀S⊂G,o(G−S)≤∣S∣展开
①若 S = ϕ S=\phi S=ϕ,则o(G-S)=o(G) ≤ \le ≤|S|成立.
②若 S ≠ ϕ , 设 G − S 的奇连通片分别为 G 1 , G 2 , . . . , G n . S\ne\phi,设G-S的奇连通片分别为G_1,G_2,...,G_n. S=ϕ,设G−S的奇连通片分别为G1,G2,...,Gn.
③令 m i 是一端在 S , 一端在 G i 的边的集合 , m_i是一端在S,一端在G_i的边的集合, mi是一端在S,一端在Gi的边的集合,
{ m i ≥ k − 1 m i = k V ( G i ) − 2 E ( G i ) → m i 与 k 同奇偶 → m i ≥ k \begin{cases}m_i\ge k-1\\m_i=kV(G_i)-2E(G_i)\to m_i与k同奇偶\end{cases}\to m_i\ge k {mi≥k−1mi=kV(Gi)−2E(Gi)→mi与k同奇偶→mi≥k
④ { Σ i = 1 n m i ≥ k n Σ i = 1 n m i ≤ k ∣ S ∣ → n ≤ ∣ S ∣ , 即 o ( G − S ) ≤ ∣ S ∣ \begin{cases}\Sigma_{i=1}^{n}m_i\ge kn\\\Sigma_{i=1}^{n}m_i\le k|S|\end{cases}\to n\le |S|, 即o(G-S)\le |S| {Σi=1nmi≥knΣi=1nmi≤k∣S∣→n≤∣S∣,即o(G−S)≤∣S∣
由Tutte定理知,G中有完备匹配.
15.证明树有完备匹配的充要条件是 ∀ v ∈ V ( G ) , o ( G − v ) = 1. \forall v\in V(G), o(G-v)=1. ∀v∈V(G),o(G−v)=1.
必要性:
若 树 G 有完备匹配 M 树G有完备匹配M 树G有完备匹配M,
①由 M M M导出子图 H H H,()=(), ()=()=0.
②∀∈(),(−)=1。(−)≤(−)=1.
③又(−)≥1.故(−)=1.
充分性:
若∀∈(),(−)=1,下证G有完备匹配。
①(−)中的奇连通片有且仅有1个,故该连通片可表示为(),
v与()之间的边同样有且仅有1个,故可表示为()=,
②同理,(−)=1.与()之间的边为()=,则边构成u和v的匹配边。
③M={m(v) | v∈V(G)}为完备匹配(m(v)=m(u),集合需要去重)
16.对二分图进行 δ \delta δ边着色,能使得每顶所关联的边中皆出现 δ \delta δ种颜色.
设 C 是二分图 G C是二分图G C是二分图G的一个最佳 δ \delta δ边着色.
①若存在顶 v v v, 满足 c ( v ) < δ c(v)<\delta c(v)<δ
②则v上存在一种颜色关联0次,一种颜色关联至少2次,满足引理5.2的条件. 于是G中存在奇圈.则G不是二分图, 与题意矛盾.
故假设①不成立.原命题成立.
17.G是奇数个顶的k次正则图(k>0),则 χ ′ ( G ) = Δ + 1 \chi'(G)=\Delta+1 χ′(G)=Δ+1
(边正常着色对应匹配边)
①在正常边着色中, 同色边对应一组匹配, 当顶点数为奇数时, 匹配边 ≤ v − 1 2 \le \frac{v-1}{2} ≤2v−1
②故 同色边条数 ≤ v − 1 2 → ε ≤ χ ′ v − 1 2 → k v 2 ≤ χ ′ v − 1 2 → k > χ ′ 同色边条数\le \frac{v-1}{2}\to \varepsilon\le\chi'\frac{v-1}{2}\to k\frac{v}2\le \chi'\frac{v-1}{2}\to k>\chi' 同色边条数≤2v−1→ε≤χ′2v−1→k2v≤χ′2v−1→k>χ′
③即 Δ > χ ′ . \Delta>\chi'. Δ>χ′.又因为 χ ′ ∈ { Δ , Δ + 1 } , 故 χ ′ = Δ + 1 \chi'\in\{\Delta,\Delta+1\},故\chi'=\Delta+1 χ′∈{Δ,Δ+1},故χ′=Δ+1
18.若G中任二奇圈皆有公共顶点,则 χ ( G ) ≤ 5. \chi(G)\le5. χ(G)≤5.
①.若 χ ( G ) ≥ 6 \chi(G)\ge6 χ(G)≥6, 设G的 χ \chi χ顶正常着色为( V 1 , V 2 , . . , V χ V_1,V_2,..,V_{\chi} V1,V2,..,Vχ).
②. G ′ = G [ V 1 ∪ V 2 ∪ V 3 ] 为 G 的导出子图 G'=G[V_1\cup V_2\cup V_3]为G的导出子图 G′=G[V1∪V2∪V3]为G的导出子图, χ ( G ′ ) = 3 → G ′ 不是二分图 → G ′ 存在奇圈 C 1 \chi(G')=3\to G'不是二分图\to G'存在奇圈C_1 χ(G′)=3→G′不是二分图→G′存在奇圈C1.
③同理.令 G ′ ′ = G [ V 4 ∪ V 5 ∪ . . . ∪ V χ ] , G''=G[V_4\cup V_5 \cup ...\cup V_{\chi}], G′′=G[V4∪V5∪...∪Vχ],有 χ ( G ′ ′ ) ≥ 3 → G ′ 不是二分图 → G ′ 存在奇圈 C 2 \chi(G'')\ge3\to G'不是二分图\to G'存在奇圈C_2 χ(G′′)≥3→G′不是二分图→G′存在奇圈C2.
④则G中存在两个奇圈 C 1 , C 2 且 C 1 , C 2 无公共顶点 C_1,C_2且C_1,C_2无公共顶点 C1,C2且C1,C2无公共顶点,与已知矛盾.
故假设①不成立.原命题成立.
19.对G的任意子图H都有 α ( H ) ≥ ∣ V ( H ) ∣ 2 , \alpha(H)\ge\frac{|V(H)|}{2}, α(H)≥2∣V(H)∣,则G是二分图.
①假设 G 中存在奇圈 C , C 是 G 的一个子图 . G中存在奇圈C,C是G的一个子图. G中存在奇圈C,C是G的一个子图.
② α ( C ) = ∣ V ( C ) ∣ − 1 2 < ∣ V ( G ) ∣ 2 \alpha(C)=\frac{|V(C)|-1}{2}<\frac{|V(G)|}{2} α(C)=2∣V(C)∣−1<2∣V(G)∣,与已知矛盾
故假设①不成立,G不存在奇圈 → \to →G是二分图.
20.顶数2k-1的k次正则图G是Hamilton图( k ≥ 2 k\ge2 k≥2)
{ V ( G ) ∣ = 2 k − 1 ( k ≥ 2 ) , 则 ∣ V ( G ) ∣ ≥ 3 ∀ u , v ∈ G , 2 k = d ( u ) + d ( v ) > ∣ V ( G ) ∣ → G 满足 O r e 定理 \begin{cases}V(G)|=2k-1(k\ge2),则|V(G)|\ge3\\\forall u,v\in G,2k=d(u)+d(v)>|V(G)|\end{cases}\to G满足Ore定理 {V(G)∣=2k−1(k≥2),则∣V(G)∣≥3∀u,v∈G,2k=d(u)+d(v)>∣V(G)∣→G满足Ore定理
故G是Hamilton图.
21.若 u , v ∈ V ( G ) u,v\in V(G) u,v∈V(G), u , v u,v u,v不相邻,且 d ( v ) + d ( u ) ≥ ∣ V ( G ) ∣ d(v)+d(u)\ge |V(G)| d(v)+d(u)≥∣V(G)∣,且 G + u v G+uv G+uv是 H a m i l t o n Hamilton Hamilton图,证 G G G也是 H a m i l t o n Hamilton Hamilton图.
G 存在 H a m i l t o n 轨 P = v 1 v 2 . . . v n . 令 u = v 1 , v = v n G存在Hamilton轨P=v_1v_2...v_n.令u=v_1,v=v_n G存在Hamilton轨P=v1v2...vn.令u=v1,v=vn
①假设 G G G中不存在 H a m i l t o n Hamilton Hamilton回路
②对 ∀ i ∈ [ 2 , n − 1 ] , i ∈ N + , 若 v 1 , v i 邻接 , 则 v i − 1 , v n 不邻接 \forall i\in[2,n-1],i\in N^+,若v_1,v_i邻接,则v_{i-1},v_n不邻接 ∀i∈[2,n−1],i∈N+,若v1,vi邻接,则vi−1,vn不邻接,否则存在Hamilton回路 P ′ = v 1 v 2 . . . v i − 1 v n v n − 1 . . . v i v 1 . P'=v_1v_2...v_{i-1}v_nv_{n-1}...v_iv_1. P′=v1v2...vi−1vnvn−1...viv1.
③则 d ( v n ) ≤ ( ∣ V ( G ) ∣ − 1 ) − d ( v 1 ) d(v_n)\le (|V(G)|-1)-d(v_1) d(vn)≤(∣V(G)∣−1)−d(v1),即 d ( v ) + d ( u ) < ∣ V ( G ) ∣ d(v)+d(u)<|V(G)| d(v)+d(u)<∣V(G)∣,与已知矛盾
故假设①不成立. 原命题成立.