【LeetCode: 73. 矩阵置零 + 矩阵】

算法题

算法刷题专栏 | 面试必备算法 | 面试高频算法
越难的东西,越要努力坚持，因为它具有很高的价值，算法就是这样✨
作者简介：硕风和炜，CSDN-Java领域优质创作者，保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享
恭喜你发现一枚宝藏博主,赶快收入囊中吧
人生如棋，我愿为卒，行动虽慢，可谁曾见我后退一步？

算法题

题目链接

• 73. 矩阵置零

⛲ 题目描述

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

示例 1：

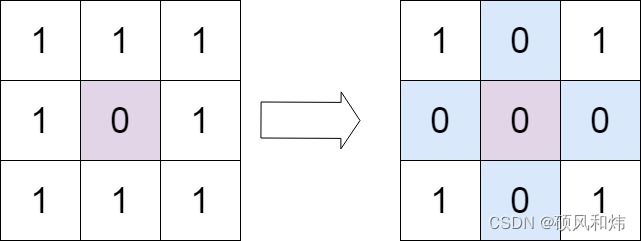
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

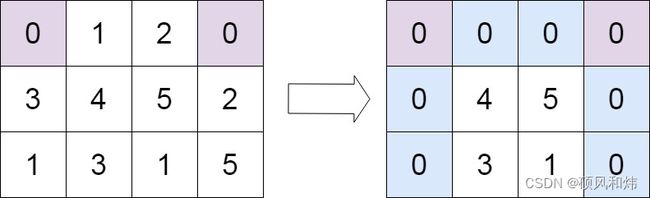
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

提示：

m == matrix.length
n == matrix[0].length
1 <= m, n <= 200
-231 <= matrix[i][j] <= 231 - 1

进阶：

一个直观的解决方案是使用 O(mn) 的额外空间，但这并不是一个好的解决方案。
一个简单的改进方案是使用 O(m + n) 的额外空间，但这仍然不是最好的解决方案。
你能想出一个仅使用常量空间的解决方案吗？

求解思路&实现代码&运行结果

---

⚡ 矩阵

求解思路

1. 解法一：开辟俩个额外的数组空间，比较什么哪一个位置需要置为0，然后模拟遍历即可。
2. 解法二：使用俩个变量，先分别表示首行首列的元素是否需要置为0，然后遍历非首行首列的元素，如果找到为0的位置，将需要更新的信息放到首行首列上，然后根据标记的结果，再次遍历，更新非首行首列的元素。最后，更新首行首列的元素。
3. 解法三：在解法二的基础上，改进为只需要一个列变量，就可以标记所有的位置信息，为什么呢？因为第一行是否有0可以存储到第一行第一列的位置。
4. 有了基本的思路，接下来我们就来通过代码来实现一下。

实现代码

解法一

class Solution {
    public void setZeroes(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        boolean[] row = new boolean[m];
        boolean[] col = new boolean[n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == 0) {
                    row[i] = col[j] = true;
                }
            }
        }
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (row[i] || col[j]) {
                    matrix[i][j] = 0;
                }
            }
        }
    }
}

解法二

class Solution {
    public void setZeroes(int[][] matrix) {
        boolean row0Zero = false;
        boolean col0Zero = false;
        int i = 0;
        int j = 0;
        for (i = 0; i < matrix[0].length; i++) {
            if (matrix[0][i] == 0) {
                row0Zero = true;
                break;
            }
        }
        for (i = 0; i < matrix.length; i++) {
            if (matrix[i][0] == 0) {
                col0Zero = true;
                break;
            }
        }
        for (i = 1; i < matrix.length; i++) {
            for (j = 1; j < matrix[0].length; j++) {
                if (matrix[i][j] == 0) {
                    matrix[i][0] = 0;
                    matrix[0][j] = 0;
                }
            }
        }
        for (i = 1; i < matrix.length; i++) {
            for (j = 1; j < matrix[0].length; j++) {
                if (matrix[i][0] == 0 || matrix[0][j] == 0) {
                    matrix[i][j] = 0;
                }
            }
        }
        if (row0Zero) {
            for (i = 0; i < matrix[0].length; i++) {
                matrix[0][i] = 0;
            }
        }
        if (col0Zero) {
            for (i = 0; i < matrix.length; i++) {
                matrix[i][0] = 0;
            }
        }
    }
}

解法三

class Solution {
	public void setZeroes(int[][] matrix) {
		boolean col0 = false;
		int i = 0;
		int j = 0;
		for (i = 0; i < matrix.length; i++) {
			for (j = 0; j < matrix[0].length; j++) {
				if (matrix[i][j] == 0) {
					matrix[i][0] = 0;
					if (j == 0) {
						col0 = true;
					} else {
						matrix[0][j] = 0;
					}
				}
			}
		}
		for (i = matrix.length - 1; i >= 0; i--) {
			for (j = 1; j < matrix[0].length; j++) {
				if (matrix[i][0] == 0 || matrix[0][j] == 0) {
					matrix[i][j] = 0;
				}
			}
		}
		if (col0) {
			for (i = 0; i < matrix.length; i++) {
				matrix[i][0] = 0;
			}
		}
	}
}

运行结果

解法一

解法二

解法三

---

共勉

最后，我想和大家分享一句一直激励我的座右铭，希望可以与大家共勉！