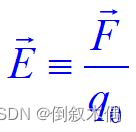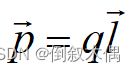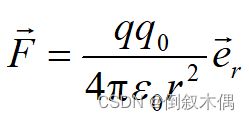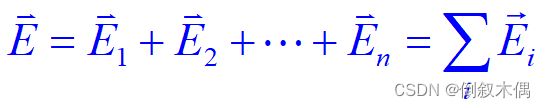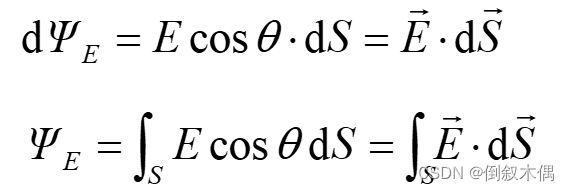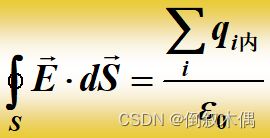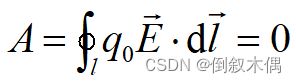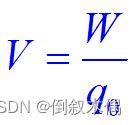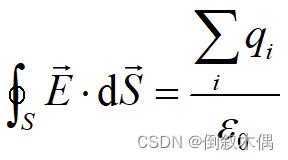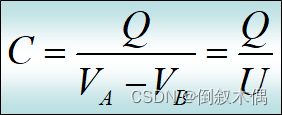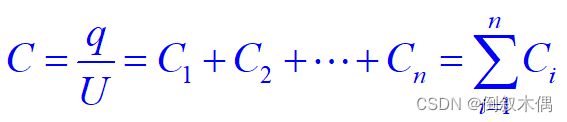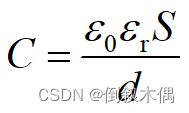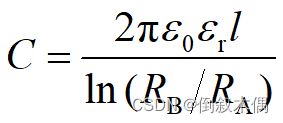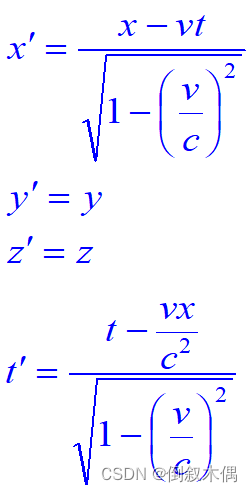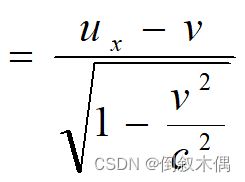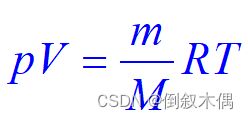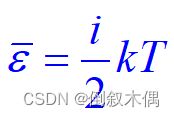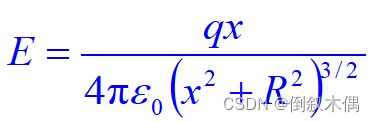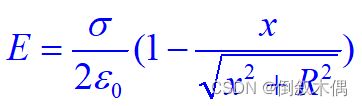大学物理C 期末考试 笔记总结(上)【个人复习向】【欢迎各位斧正错误之处】
笔记知识点：
1.守恒定律：
机械能守恒：如果一个系统内只有保守力做功，其他内力和外力都不做功，则系统内各个物体的动能和势能可以相互转换，但机械能总值不变
动量守恒定律：如果系统所受到的外力为零，系统的总动量保持不变
定轴转动的角动量守恒：物体在定轴转动中，当对转轴的合外力矩为零时，物体对转轴的角动量保持不变。
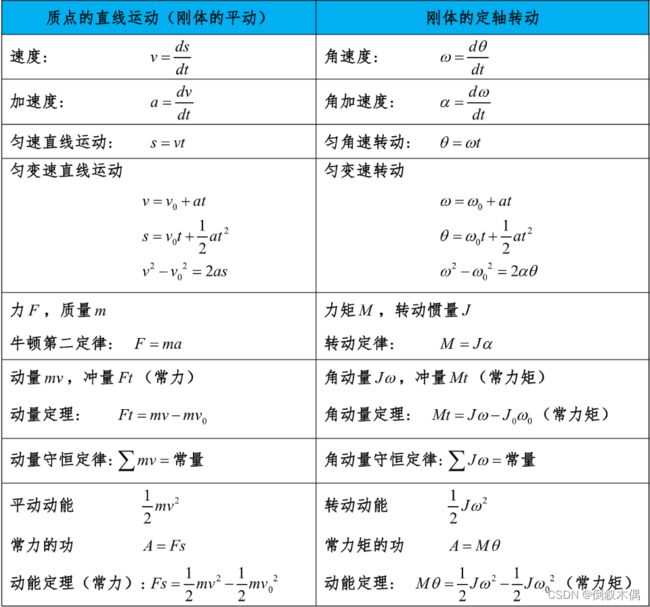
2.刚体平动和转动的重要公式
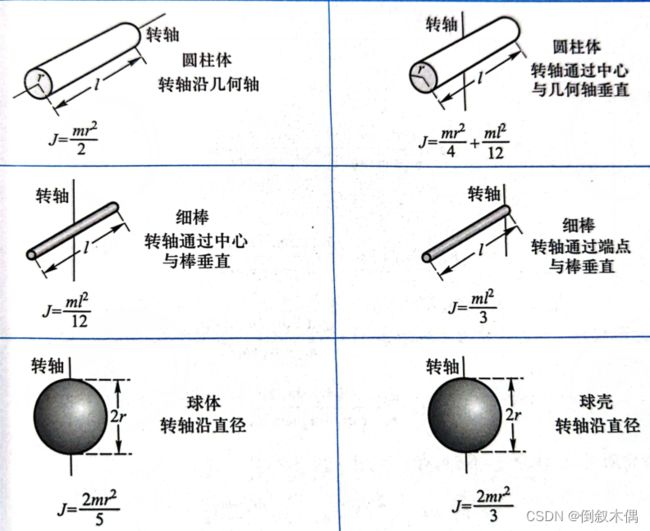
3.常见的转动惯量
4.库仑定律：
5.电场
电场是一种物质，静电场时静止电荷所产生的电场，电荷再电场中受到电场力的作用。电场力有对电荷做功的本领。
6.电流
电流是由大量电荷作有规律的定向运动所导致的
大小等于从垂直于电荷运动方向上的单位界面流过的电流
注意：电流密度矢量
电流与密度的关系式为：
7.电荷
电荷守恒定律：在一个与外界没有电荷交换的系统内，无论进行怎样的物理过程，系统内正、负电荷量的代数和总是保持不变。
点电荷的定义：物理学上把本身的线度比相互之间的距离小得多的带电体叫做点电荷。相当于运动学的“质点”模型。
1913年，密立根进行液滴实验，证明了微小油滴所带电荷量的变化不连续，即为元电荷e的整数倍。
8.库伦定律
真空中两个静止点电荷相互作用力（静电力）的大小与这两个点电荷所带电荷量q1和q2的乘积成正比，与它们之间的距离r 的平方成反比。作用力的方向沿它们的连线方向，同号相斥，异号相吸。
真空介电常量：e0 = 8.85´10-12 C2 ·N-1·m-2
注意：该定律适用于点电荷，同时该定理具有一定误差，可使用静电力叠加定理
9.电场
静电场：静电荷所产生的电场
电场的两个重要性质：电荷在电场中要受到电场力的作用，电场力对电荷有做功的本领
电场强度：
（与q0无关，定义式）
场强的方向：试验电荷在该处所受电场力的方向。
注意：点电荷q在外场中受的电场力： 
SI单位一般为N/C或V/m
10.电场线
描述电场分布的一系列有向曲线
1. 曲线上每一点的切线方向表示该点电场强度 的方向
2. 曲线的疏密表示该点处场强 的大小。
注意：一个金属球带上正电荷后，该球质量减小（带正电荷失去电子）
11.电偶极子
大小相等、符号相反并有一微小间距的两个点电荷构成的复合体
电偶极矩（electric moment）：
注意：电偶极子在非均匀外电场中如何运动？在非均匀外电场中，电偶极子所受合外力不为0，力矩不为0，电偶极子在非均与外电场中既转动又平动
（注意极子的极矩的方向与场强方向的关系）
12.电场强度的计算
点电荷的电场强度
场强叠加原理和点电荷系的电场强度
电荷连续分布带电体的电场强度：
（1）电荷元dq在P点的电场强度：
（2）带电体在P点的电场强度：
体电荷：dq =rdV
面电荷：dq=sdS
线电荷： dq =ldl
13.电场线：描述电场分布的一系列有向曲线
曲线上每一点的切线方向表示该点电场强度 E的方向
曲线的疏密表示该点处场强 E的大小。即：通过垂直单位面积的电场线条数，在数值上就等于该点处电场强度的大小
静电场中电场线的特点：电场线起始于正电荷，终止于负电荷；电场线不闭合，不相交；电场线密集处电场强，电场线稀疏处电场弱
注意: 电场线并不是实际存在的, 只是形象描述电场的几何方法。
14.电场强度通量
：
定义：通过电场中任意一个曲面的电场线条数
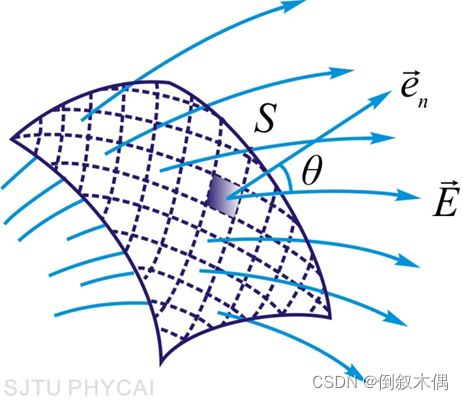
均匀电场中通过平面S的电场强度通量
非均匀电场的电场强度通量
对闭合曲面的电通量：
注意：规定闭合曲面以外法线方向为正
15.静电场的高斯定理
高斯定理可以由库仑定律和电场强度叠加原理推导出
通过任一个包围点电荷的闭合曲面的电通量与曲面无关，结果都等于
一般情况：
任意电荷系产生的电场,
高斯面为任意闭合曲面
高斯定理的应用
高斯定理的一个重要应用是：
计算带电体周围电场的电场强度。
只有在场强分布具有一定的对称性时，才能比较方便应用高斯定理求出场强。
求解的关键是选取适当的高斯面。
常见的具有对称性分布的源电荷有：
球对称：如均匀带电的球体、球面、球壳。
轴对称：如均匀带电的长直柱体、柱面。
平面对称：如均匀带电的无限大平面、平板。
用高斯定理计算场强的步骤：
1）分析场强分布的对称性，找出场强的方向和场强大小的分布。
2）选择适当的高斯面，并写出通过该高斯面的电通量。
3）求出高斯面所包围的电量。
4）按高斯定理求出场强。
如何选取高斯面：
1）高斯面必须是闭合曲面；
2）高斯面必须通过所求的场点；
3）高斯面的形状必须简单规则，以便于计算穿过该面的电通量。
4）使高斯面上各点的场强大小相等，方向与高斯面法线方向一致。
或高斯面上某一部分各点的场强方向与高斯面法线方向垂直，该部分的通量为零。而另一部分各点的场强大小相等，方向与高斯面法线方向一致。
无限大均匀带电平面的场强
15.静电场的环路定理 电势
静电力做功：
点电荷场力做功与具体路径无关，同时，试验电荷在静电场中移动时，电场力所做的功只与试验电荷的起点和终点的位置有关，而与路径无关，即静电场力是保守力。
由于q0不等于零，因此
静电场中电场强度的环流为零, 称静电场的环流定理。
16.电势
对于保守力场，可以引入势能的概念——电势能
电势：
静电场中a、b两点的电势差，等于将单位正电荷从a点移至b点电场力所做的功。
视分析问题方便，可以任意选择电势零点。选择不同的电势零点，给定电场的电势描述不同！但任意两点间的电势差是保持不变的！
约定：在理论计算时，对有限带电体电势选无限远为参考点；在实际应用中，取大地、仪器外壳等为电势零点。
电势计算的两种方法:
（一）已知电场强度分布, 由电势的定义计算:
（二）从点电荷的电势出发, 应用电势叠加原理计算任何有限分布电荷系统的电势。
点电荷的电势：
点电荷的电势是球对称的，对称中心在点电荷处。
电势是标量，正负与电荷及电势零点选择有关
17.等势面
将电势相等的场点连成更连续的曲面---等势面
约定：相邻等势面的电势差为常量，可以得到一系列的等势面
等势面的性质：
1. 电荷沿等势面移动，电场力不做功。（电荷在场强为零的区域移动，电场力不做功。）
2. 电场强度与等势面正交；电场线由电势高的地方指向电势低的地方。
3. 等势面密集处场强量值大，稀疏处场强量值小。
18.静电场中的导体
静电场与物质的相互作用问题：
（1）物质在静电场中要受到电场的作用，表现出宏观电学性质；
（2）物质的电学行为也会影响电场分布，最后达到静电平衡状态。
理论基础为静电场的高斯定理
导体的静待平衡：导体内部和表面上任何一部分都没有宏观电荷运动，我们就说导体处于静电平衡状态
导体的经典平衡性质：
1. 导体内部和导体表面处处电势相等，整个导体是个等势体，导体表面成为等势面。
2. 导体内部的电场强度处处为零。导体表面的电场强度垂直于导体的表面。
静电平衡下导体上的电荷分布
在静电平衡下，导体所带的电荷只能分布在导体的外表面，导体内部没有净电荷。
2. 静电平衡下的孤立导体，其表面处电荷面密度s与该表面曲率有关，曲率（1/R）越大的地方电荷面密度也越大，曲率越小的地方电荷面密度也小。当表面凹进，曲率为负值时，电荷面密度更小。
3. 孤立的带电导体球、 长直圆柱、 无限大平板表面电荷均匀分布。
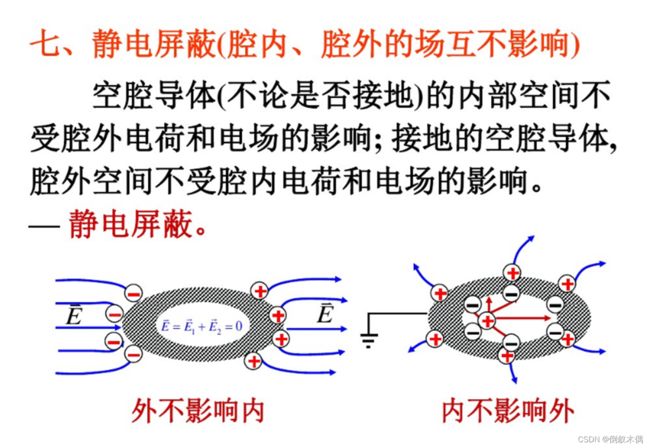
空腔导体内外的静电场与静电屏蔽
此外，处于静电平衡的导体，其表面上各点的电荷密度与表面邻近处场强的大小成正比。
18.电容器的电容
孤立导体的电容：
孤立导体的电势与电荷量有关：
电荷量相同时不同形状和大小的孤立导体电势不同，但是V正相关q
定义C恒等于q/v（孤立导体的电容）
电容只与导体的几何因素（及周围介质）有关，反映导体带电多少的本领——固有的容电本领
SI：F（法拉）
电容器的电容”：
电容的大小仅仅与导体的形状，相对位置有关，与其间的电介质有关，与所带的电荷量无关
（
）
电容器电容的计算
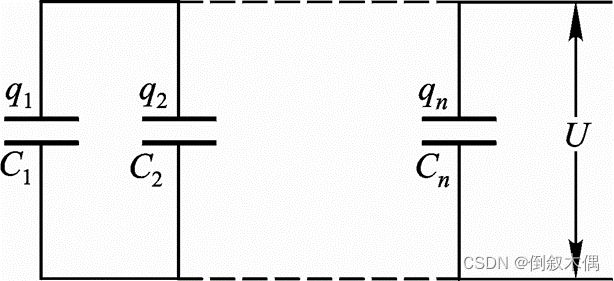
19.电容器的串并联
电容器的并联
电容器的串联
实验证明，充满电介质时电容器的电容C为两极板间为真空时电容C0的er倍：
（适用于任何形状的电容器）
er称为介质的相对电容率或相对介电常量。
如果两极板间充满相对电容率为er的电介质，各种电容器的电容C 为
平板电容器：
球形电容器：
圆柱形电容器：
20.狭义相对论
相对性原则：一切物理规律在任何惯性系中形式相同
光速不变原理：在所有惯性系中，真空中的光速相同，与光源和观测者的运动无关
狭义相对性原理是伽利略相对性原理的推广
光速不变与伽利略变换相矛盾，与实验结果相符，指出了伽利略变换的局限性，必须用新的变换来代替——洛伦兹变换。
两个基本假设最终否定了牛顿的绝对时空观，而必须代之以新的时空观——相对时空观。
21.洛伦兹变换
惯性系[K] : P(x, y, z; t)«惯性系[K´]: P(x´, y´, z´; t´)
注意：空间坐标与时间坐标相互关联。
要求 v<c， 指出了极限速度——真空中的光速c。
v<<c时，即 v/c®0 时，变为伽利略变换
22.相对论速度变换
速度的定义：
由洛伦兹力可以得出：
23.时间延缓
在K´系的观测者看来，运动的钟变慢了，称为动钟变慢，又称时间延缓或时间膨胀。
动钟变慢是相对论的时空效应，与钟的具体结构和其他外界因素无关。
•现代物理实验为相对论的时间延缓提供了有力的证据。
24.长度收缩
长度的定义：长度是用一种空间，来测量另一种（一维）空间，其测量值就是长度
长度 = 在与长度方向平行的坐标轴上，物体两端坐标值之差
当物体静止时，两端坐标不需要同时记录；
当物体运动时，两端坐标必须同时记录。
长度测量与被测物体相对于观察者的运动有关，物体在运动方向长度缩短了， 而在垂直于运动方向上，长度不会收缩。
同时，要注意的是：
如：第二宇宙速度 v =11.2´103 m/s ， v/c » 10-4
• 测量效应与视觉效应不同。
• 长度收缩与动钟延缓效应是相关的、一致的。
25.“同时”的相对性（relativity of simultaneity）
K系:同时不同地的两个事件,
在K’系是既不同时也不同地的两个事件.
K系:同时也同地的两个事件,
在K’系才是同时也同地的两个事件.
要注意的是：
1.不同参考系,对运动过程的(时空)描述不同;
2.时空是相对的，事件的结果是绝对的
26.相对性与绝对性
相对性：在相对论时空中，运动的描述、时空的量度都是相对的。
绝对性：事件的因果关系有绝对意义。
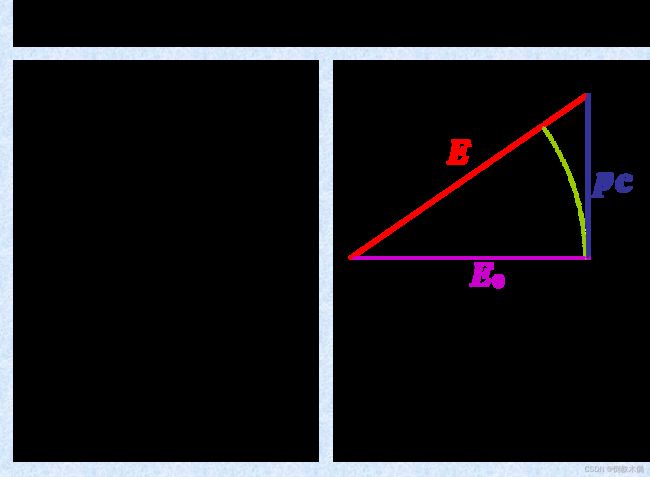
27.狭义相对论动力学
28.热运动
热运动的描述：
状态参数：为了描述物体的状态，常采用一些物理量来表示物体的有关特性，例如体积、温度、压强、密度等，称状态参量（state parameter）。
体积V 气体分子所能达到的空间
压强p 气体分子垂直作用于器壁单位面积上的
力，是大量气体分子与器壁碰撞的宏观
表现。 1atm =760 mmHg =1.01´105 Pa
平衡态：平衡态（equilibrium state）：在不受外界影响（即系统与外界没有物质和能量的交换）的条件下，无论初始状态如何，系统的宏观性质在经充分长时间后不再发生变化的状态。
当气体的外界条件改变时，气体从一个状态不断地变化到另一状态，如果状态变化过程进展得十分缓慢，使所经历的一系列中间状态，都无限接近平衡状态，这个过程就叫做准静态过程（quasi-static process）或平衡过程（equilibrium process）。
29.理想气体物态方程
理想气体：在任何情况下都严格遵守波意耳定律、盖吕萨克定律以及查理定律的气体。是实际气体在压强趋于零时的极限。
当质量为m、摩尔质量为Ｍ的理想气体处于平衡态时，它的状态参量（p、 V、T） 满足方程：
需要注意的是：标准状态下 ，气体分子之间的距离大约是分子本身线度（10-10 m）的10倍左右，可把气体看作是彼此相距很大间隔的分子集合；分子与分子间的相互作用力，除了在碰撞的瞬间以外，极为微小。
分子热运动的平均速度约 = 500 m/s ，
分子的平均碰撞频率约 = 1010 /s，
分子的平均自由程约 =10-7 m。
30.分子热运动的基本特征
基本特征：分子的永恒运动与频繁的相互碰撞
注意：分子热运动与机械运动有本质的区别，分子运动具有无序性，还具有统计性
（上图为布朗运动）
31.理想气体
微观模型：
力学假设：分子线度与分子间距相比较可忽略，分子被看作质点。除了分子碰撞的瞬间外，忽略分子间的相互作用。气体分子在运动中遵守经典力学规律，假设碰撞为弹性碰撞。一般情况，忽略分子的重力。
可概括为：理想气体分子是自由地无规则地运动着的弹性质点群。
统计假设：平衡态时， 气体分子数密度 n 分布均匀。平衡态时，相同速率的分子沿各个方向运动的平均分子数相等(或沿各方向运动的概率均等)。
32.能量均分定理：
分子的自由度：自由度是决定某物体在空间的位置所需要的独立坐标数目。
运动刚体的自由度：随质心的平动+绕过质心轴的转动
自由刚体有 6个自由度，但是刚性细棒只有5个自由度（3个平动自由度 + 2个转动自由度）
分子的平均平动动能 3kT/2 是均匀地分配在每个平动自由度上的, 每个平动自由度都具有相同的平均动能 kT/2 . 推广到分子的转动和振动上，得到能量按自由度均分的统计规律——能量均分定理：在温度为 T 的平衡态下，物质分子的每一个自由度都具有相同的平均动能，其大小都等于kT/2。
（i为刚性分子的自由度）
如果考虑振动，那么每个振动自由度上均分有kT/2的振动势能
33.如何求电场强度？
练习题
第一章
1.
2.
3.
速度的变化率是切向加速度的分量，位置矢量的变化率是速度
4.
求质点的运动轨迹本质上是找出x与y的关系
5.
求各个数据的关系时，可以考虑将两边求积分，然后再求两边对应的关系
第四章
第七章
1.真空中有均匀带电直线，长为L，总电荷为q。线外有一点P，离开直线的垂直距离为a，P点和直线两端连线的夹角分别为q1和q2 ，求P点的电场强度。（设电荷线密度为l）
讨论：因此无限长的带点导线（直线），若q1 = 0 ，q2 = Π
当 a®0 时,
若P点在直线上: q1 = 0，q2 = Π , 则 E®∞, 无意义，
若P点在直线延长线上时，积分上下限q1 = q2 = 0, 应当重新积分计算。
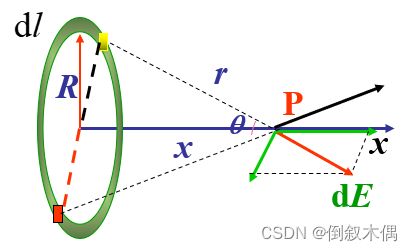
2.电荷q 均匀地分布在一半径为R 的圆环上，计算在圆环的轴线上任一给定点P 的电场强度。
讨论：若x=0，则E=0，环心处的电场强度为0.若x远大于R则有
（远离圆环处的场强近似等于点电荷的电场强度）
3.求均匀带电圆盘轴线上任一点的电场。设盘半径为R，电荷面密度为s
均匀带电的薄圆盘可看成由许多带电细圆环组成。
