最长公共子序列 - LCS

问题描述

子序列定义

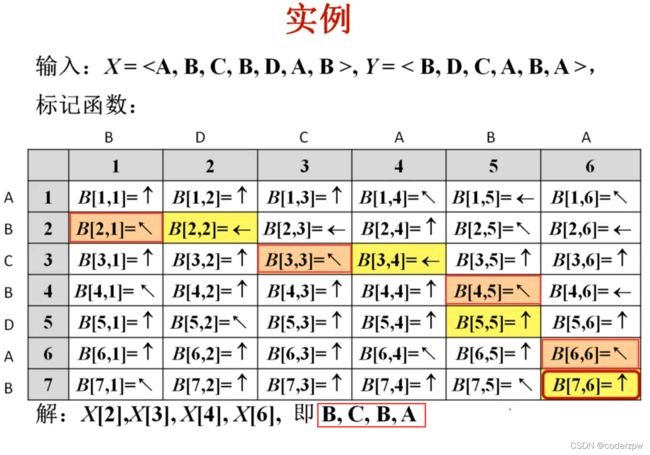
给定一个序列X=，另一个序列Z=，若存在一个严格递增的X的下标序列对所有的1,2,3,…,k，都满足x(ik)=zk，则称Z是X的子序列

比如Z=是X=B,C,B,D,A,B>的子序列

子串定义

子串的话与子序列不同，子串要求必须连续。

例如
BCDB 虽然是X=B,C,B,D,A,B>的子序列
但不是它的字串 因为BCDB不连续。
而BCBD属于B,C,B,D,A,B>的字串

该篇文章我们要求的是 子序列 而不是 子串

公共子序列定义

如果Z既是X的子序列，又是Y的子序列，则称Z为X和Y的公共子序列

最长公共子序列（以下简称LCS）

2个序列的公共子序列中长度最长的那个

动态规划解决

子问题划分及依赖关系

递推公式

伪代码

利用标记函数追踪解：

代码实现

public class LCS {

    public static void main(String[] args) {
        String x = "ABCBDAB";
        String y = "BDCABA";

        int m = x.length();
        int n = y.length();

        // 动态数组
        int[][] c = new int[m+1][n+1];
        // 标记函数数组
        int[][] b = new int[m+1][n+1];

        // 上边界赋值为0
        for (int i=0; i<=n; i++) {
            c[0][i] = 0;
            b[0][i] = 0;
        }
        // 左边界赋值为0
        for (int i=0; i<=m; i++) {
            c[i][0] = 0;
            b[i][0] = 0;
        }

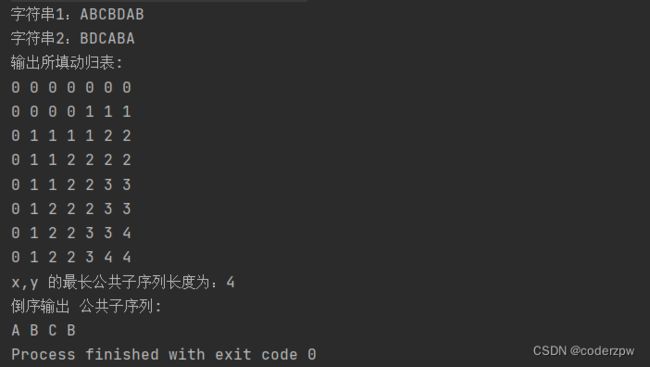
        System.out.println("字符串1：" + x);
        System.out.println("字符串2：" + y);

        LCSlength(m, n, x, y, c, b);
        System.out.println("x,y 的最长公共子序列长度为：" +  c[m][n]);

        // 倒序输出 公共子序列
        System.out.println("倒序输出 公共子序列:");
        LCS(m, n, b, x);
    }

    /**
     * 最长公共子序列
     */
    public static void LCSlength(int m, int n, String x, String y, int[][] c, int[][] b) {

        for (int i=1; i<=m; i++) {
            for (int j=1; j<=n; j++) {
                if (x.charAt(i-1) == y.charAt(j-1)) {   // 若字符相同 c[i][j] = c[i-1][j-1] + 1;
                    c[i][j] = c[i-1][j-1] + 1;
                    b[i][j] = 1;    // 1 代表 ↖
                } else if (c[i][j-1] > c[i-1][j]) { // 字符不同取最大 c[i][j] = max(c[i][j-1], c[i-1][j])
                    c[i][j] = c[i][j-1];
                    b[i][j] = 2;    // 2 代表 ←
                } else {
                    c[i][j] = c[i-1][j];
                    b[i][j] = 3;    // 3 代表 ↑
                }
            }
        }
        // 输出所填表
        System.out.println("输出所填动归表:");
        for (int i=0; i<=m; i++) {
            for (int j=0; j<=n; j++) {
                System.out.print(c[i][j] + " ");
            }
            System.out.println();
        }


    }

    /**
     * 输出 最长公共子序列 倒序输出
     * @param i
     * @param j
     * @param b：标记函数数组
     * @param x：x字符串
     */
    public static void LCS(int i, int j, int[][] b, String x) {

        if (i==0 || j==0) {
            return;
        }

        //  1 表示 ↖
        if (b[i][j] == 1) {
            System.out.print(x.charAt(i-1) + " ");
            // 输出该字符
            LCS(i-1, j-1, b, x);
        } else if (b[i][j] == 2) {  // 2 表示 ←
            LCS(i, j-1, b, x);
        } else {                    // 3 表示 ↑
            LCS(i-1, j, b, x);
        }
    }
}

输出结果：

复杂度分析

时间复杂度： O(mn) 两层循环
空间复杂度： O(mn) 需要一个二维数组的表格