POJ2635 The Embarrassed Cryptographer

POJ2635 The Embarrassed Cryptographer

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 8683		Accepted: 2231

Description

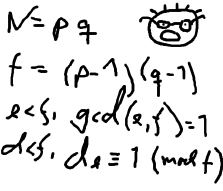The young and very promising cryptographer Odd Even has implemented the security module of a large system with thousands of users, which is now in use in his company. The cryptographic keys are created from the product of two primes, and are believed to be secure because there is no known method for factoring such a product effectively. 
What Odd Even did not think of, was that both factors in a key should be large, not just their product. It is now possible that some of the users of the system have weak keys. In a desperate attempt not to be fired, Odd Even secretly goes through all the users keys, to check if they are strong enough. He uses his very poweful Atari, and is especially careful when checking his boss' key.

Input

The input consists of no more than 20 test cases. Each test case is a line with the integers 4 <= K <= 10¹⁰⁰ and 2 <= L <= 10⁶. K is the key itself, a product of two primes. L is the wanted minimum size of the factors in the key. The input set is terminated by a case where K = 0 and L = 0.

Output

For each number K, if one of its factors are strictly less than the required L, your program should output "BAD p", where p is the smallest factor in K. Otherwise, it should output "GOOD". Cases should be separated by a line-break.

Sample Input

143 10

143 20

667 20

667 30

2573 30

2573 40

0 0

Sample Output

GOOD

BAD 11

GOOD

BAD 23

GOOD

BAD 31

******************************************************

题目大意：给定一个大整数，这个数是两个素数的乘积，然后给定一个数L，如果这两个素数中有一个比L小，就输出BAD；不然输出GOOD

解题思路：纠结的数学，高精度求模+同余模定理

参考了：http://www.th7.cn/Program/c/2011/07/31/36753.shtml

原来，可以这样：

例如要验证123是否被3整除，只需求模123%3

但当123是一个大数时，就不能直接求，只能通过同余模定理对大数“分块”间接求模

具体做法是：

先求1%3 = 1

再求（1*10+2）%3 = 0

再求 （0*10+4）% 3 = 1

那么就间接得到124%3=1，这是显然正确的

而且不难发现， （1*10+2）*10+4 = 124

这是在10进制下的做法，千进制也同理，*10改为*1000就可以了

嗯，又学到了点。

#include <iostream>

#include <cstring>

#include <string>

#include <math.h>

#include <stdio.h>

#define N 1000001

using namespace std;



string num;

int da[105];

int n;

int isprime[N+5];

int prime[N+5];

int size;



void shaixuan(int n)

{

	size=0;

	memset(isprime,0,sizeof(isprime));

	int d=sqrt((double)n)+1;

	for(int i=2;i<=n;i++)

	{

		if(isprime[i])continue;

		prime[++size]=i;

		if(i>d)continue;

		for(int j=2*i;j<=n;j+=i)

            isprime[j]=1;

	}

}



int main()

{

    shaixuan(N);

    while(cin>>num>>n)

    {

        if(num[0]=='0'&&n==0)break;

        int k=0,len=num.size(),sum=0,xun=0;

        for(int i=len-1;i>=0;i--)

        {

            int temp=num[i]-'0';

            for(int j=1;j<=xun;j++)

                temp*=10;

            sum+=temp;

            xun++;

            if(xun==3)

            {

                da[++k]=sum;

                sum=0;

                xun=0;

            }

        }

        if(sum!=0)

            da[++k]=sum;

        int flag=0,ans;

        for(int i=1;i<=size;i++)

        {

            int m=prime[i];

            if(m>=n)break;

            int ys=0;

            for(int j=k;j>=1;j--)

                ys=(ys*1000+da[j])%m;

            if(ys==0)

            {

                ans=m;

                flag=1;

                break;

            }

        }

        if(flag)

            cout<<"BAD "<<ans<<endl;

        else

            cout<<"GOOD"<<endl;

    }

}