The LR-Parsing Algorithm

4.6.3 The LR-Parsing Algorithm

A schematic of an LR parser is shown in Fig. 4.35. It consists of an input, an output, a stack, a driver program, and a parsing table that has two parts (ACTION and GOTO). The driver program is the same for all LR parsers; only the parsing table changes from one parser to another. The parsing program reads characters from an input buffer one at a time. Where a shift-reduce parser would shift a symbol, an LR parser shifts a state. Each state summarizes the information contained in the stack below it.

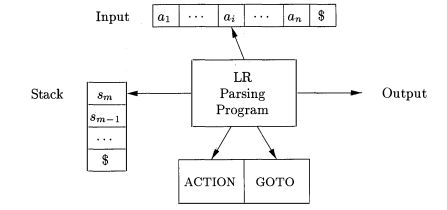
Figure 4.35: Model of an LR parser

The stack holds a sequence of states, s0s1...sm, where sm is on top. In the SLR method, the stack holds states from the LR(0) automaton; the canonical­LR and LALR methods are similar. By construction, each state has a corresponding grammar symbol. Recall that states correspond to sets of items, and that there is a transition from state i to state j if GOTO(Ii, X) = Ij. All transitions to state j must be for the same grammar symbol X. Thus, each state, except the start state 0, has a unique grammar symbol associated with it. @4

@4: The converse need not hold; that is, more than one state may have the same grammar symbol. See for example states 1 and 8 in the LR(0) automaton in Fig. 4.31, which are both entered by transitions on E, or states 2 and 9, which are both entere d by transitions on T.

Structure of the LR Parsing Table

The parsing table consists of two parts: a parsing-action function ACTION and a goto function GOTO.

1. The ACTION function takes as arguments a state i and a terminal a (or $, the input endmarker). The value of ACTION[i, a] can have one of four forms:
   1. Shift j, where j is a state. The action taken by the parser effectively shifts input a to the stack, but uses state j to represent a.
   2. Reduce A -> β. The action of the parser effectively reduces β on the top of the stack to head A.
   3. Accept. The parser accepts the input and finishes parsing
   4. Error. The parser discovers an error in its input and takes some corrective action. We shall have more to say about how such error­ recovery routines work in Sections 4.8.3 and 4.9A.
2. We extend the GOTO function, defined on sets of items, to states: if GOTO[Ii, A] = Ij, then GOTO also maps a state i and a nonterminal A to state j.

LR-Parser Configurations

To describe the behavior of an LR parser, it helps to have a notation representing the complete state of the parser: its stack and the remaining input. A configuration of an LR parser is a pair:

(s0s1...sm,aiai+1...an$)

where the first component is the stack contents (top on the right), and the second component is the remaining input. This configuration represents the right-sentential form

X1X2...Xmaiai+1...an

in essentially the same way as a shift-reduce parser would; the only difference is that instead of grammar symbols, the stack holds states from which grammar symbols can be recovered. That is, Xi is the grammar symbol represented by state si. Note that s0, the start state of the parser, does not represent a grammar symbol, and serves as a bottom-of-stack marker, as well as playing an important role in the parse.

Behavior of the LR Parser

The next move of the parser from the configuration above is determined by reading ai, the current input symbol, and sm, the state on top of the stack, and then consulting the entry ACTION[sm, ai] in the parsing action table. The configurations resulting after each of the four types of move are as follows

1. If ACTION[sm, ai] = shift s, the parser executes a shift move; it shifts the next state s onto the stack, entering the configuration
   (s0s1...sms,ai+1...an$)
   The symbol ai need not be held on the stack, since it can be recovered from s, if needed (which in practice it never is). The current input symbol is now ai+1.
2. If ACTION[sm, ai] = reduce A -> β, then the parser executes a reduce move, entering the configuration
   (s0s1...sm-rs,aiai+1...an$)
   where r is the length of β, and s = GOTO[sm-r, A]. Here the parser first popped r state symbols off the stack, exposing state Sm-r. The parser then pushed s, the entry for GOTO[sm-r, A], onto the stack. The current input symbol is not changed in a reduce move. For the LR parsers we shall construct, Xm-r+1 ··· Xm, the sequence of grammar symbols corresponding to the states popped off the stack, will always match β, the right side of the reducing production.
   The output of an LR parser is generated after a reduce move by executing the semantic action associated with the reducing production. For the time being, we shall assume the output consists of just printing the reducing production.
3. If ACTION[sm, ai] = accept, parsing is completed.
4. If ACTION[sm, ai] = error, the parser has discovered an error and calls an error recovery routine.

The LR-parsing algorithm is summarized below. All LR parsers behave in this fashion; the only difference between one LR parser and another is the information in the ACTION and GOTO fields of the parsing table.

Algorithm 4.44: LR-parsing algorithm.

INPUT: An input string ω and an LR-parsing table with functions ACTION and GOTO for a grammar G.

OUTPUT: If ω is in L(G), the reduction steps of a bottom-up parse for ω; otherwise, an error indication.

METHOD: Initially, the parser has s0 on its stack, where s0 is the initial state, and ω$ in the input buffer. The parser then executes the program in Fig. 4.36.□

let a be the first symbol of ω$;

while(true) { /* repeat forever */

    let s be the state on top of the stack;

    if ( ACTION[s, a] = shift t ) {

        push t onto the stack;

        let a be the next input symbol;

    } else if(ACTION[s, a] = reduce A -> β) {

    pop |β| symbols off the stack;

    let state t now be on top of the stack;

    push GOTO[t, A] onto the stack;

    output the production A -> β;

    } else if(ACTION[s, a] = accept) break; /* parsing is done * /

    else call error-recovery routine;

}

Figure 4.36: LR-parsing program

Example 4.45: Figure 4.37 shows the ACTION and GOTO functions of an LR-parsing table for the expression grammar (4.1), repeated here with the productions numbered:

(1) E->E+T

(2) E->T

(3) T->T*F

(4) T->F

(5) F->(E)

(6) F->id

The codes for the actions are:

1. si means shift and stack state i,
2. rj means reduce by the production numbered j,
3. acc means accept,
4. blank means error.

Note that the value of GOTO[s, a] for terminal a is found in the ACTION field connected with the shift action on input a for state s. The GOTO field gives GOTO[s, A] for nonterminals A. Although we have not yet explained how the entries for Fig. 4.37 were selected, we shall deal with this issue shortly.

STATE	ACTION						GOTO
	id	+	*	(	)	$	E	T	F
0	s5			s4			1	2	3
1		s6				acc
2		r2	s7		r2	r2
3		r4	r4		r4	r4
4	s5			s4			8	2	3
5		r6	r6		r6	r6
6	s5			s4				9	3
7	s5			s4					10
8		s6			s11
9		r1	s7		r1	r1
10		r3	r3		r3	r3
11		r5	r5		r5	r5

Figure 4.37:  Parsing table for expression grammar

On input id * id + id, the sequence of stack and input contents is shown in Fig. 4.38. Also shown for clarity, are the sequences of grammar symbols corresponding to the states held on the stack. For example, at line (1) the LR parser is in state 0, the initial state with no grammar symbol, and with id the first input symbol. The action in row 0 and column id of the action field of Fig. 4.37 is s5, meaning shift by pushing state 5. That is what has happened at line (2): the state symbol 5 has been pushed onto the stack, and id has been removed from the input.

Then, * becomes the current input symbol, and the action of state 5 on input * is to reduce by F -> id. One state symbol is popped off the stack. State 0 is then exposed. Since the goto of state 0 on F is 3, state 3 is pushed onto the stack. We now have the confi guration in line (3). Each of the remaining moves is determined similarly.□