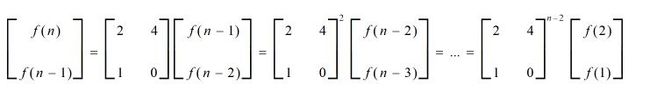递推关系转矩阵快速幂
一些递推关系如f(n) = af(n-1)+bf(n-2)+...+tf(n-k)等,在n很大的时候,O(n)的算法都不能满足要求的时候,往往可以化为矩阵快速幂来做,复杂度可以降为O(logn),大大减少了运行时间。
如何将一个递推关系式化为矩阵呢?
比如这样一个递推关系: f(n) = 2*f(n-1)+4*f(n-2)
先列出几个等式:
f(n) = 2*f(n-1)+4*f(n-2)
f(n-1) = 2*f(n-2)+4*f(n-3)
就可以将左边矩阵做n-2次幂,再乘初值,得出第一行第一个即为f(n)。
非齐次的也是如此,加一维来填1即可。
题目:HDU 4602 UVA 10870 ZOJ 3690 HDU 2971 HDU 1757