Pascal 线段树 lazy-tag 模板
先说下我的代码风格(很丑,勿喷)
maxn表示最大空间的四倍
tree数组表示求和的线段树
delta表示增减的增量标记
sign表示覆盖的标记
delta,sign实际上都是lazy标志
pushdown表示标记下传
pushup表示标记上传(即求和,区间最值)
update表示数据更新
线段树(segment tree)是一种特别有用的数据结构,我们在维护区间各种信息的时候它就是利器。可能读者嫌线段树代码太长,不想写,而树状数组代码简洁易于便携,但是我在这里想说,线段树能做到的很多东西树状数组无法做到,而若掌握了线段树的基本框架,再去写熟练的话,基本上能够做到较短的时间内DEBUG完。
我们来介绍一下什么是线段树。
问题1:
我们拥有一个数列,需要维护三个操作
1.单点修改,把a[i]的值改成v
2.区间修改,把a[i]~a[j]的值改成v
3.区间求和,求出a[i]~a[j]的和
我们不难想到使用数组存储这些东西,对于每个询问我们暴力修改,可这样的话,对于每一段区间,我们需要耗费的时间是r-l+1,当Q特别大、或者区间长度特别大的时候,时间无法忍受。这时候线段树的应用便出来了。
何谓线段树?我们把线段存储在树形结构中,利用树形结构维护线段信息的数据结构,就是线段树。
我们利用二分建树,建立一颗二叉树。为什么是二叉树呢?我个人理解是,这方便我们二分查找,二分递归,大大减少编程复杂度
而,我们每次需要的线段信息,只需要在线段树中检索, 线段树的实质是,一颗存储着线段信息的二叉搜索树。
我们把一个长的线段(区间),不断的二分划分,即[a,b]划分成[a,(a+b)>>1](leftchild),[(a+b)>>1+1,b](rightchild); 直到a=b为止。
我们把a=b的这个线段称为叶子节点。在某些题内,叶子节点存储的就是该点在线性结构所对应的信息。
由上可知,我们不断划分着[a,b]那么对于每一个[a,(a+b)>>1],[(a+b)>>1+1,b]它的左儿子和右儿子也是满足"线段树"性质
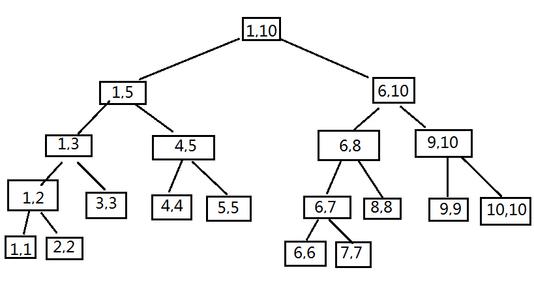
上图是我们划分[1,10]区间的过程。现在我们回到问题1
我们发现如果是一个一个叶子结点访问,那么每次访问的时间甚至比O(n)的数组模拟要长。
那么我们再看一个简单版的问题1
问题2:
给定一个序列
1.修改其中一个点
Sub:单点减小某值
Add:单点增加某值
2.询问区间和
Query:询问区间和
现在我们可以通过每次查找到叶子节点,暴力修改。
然后再递归求解区间和。
具体代码如下:
const maxn=300001; var tree:packed array [0..maxn] of longint; procedure pushup(now:longint); begin tree[now]:=tree[now<<1]+tree[now<<1+1]; //区间求和 end; procedure build(l,r,now:longint); var mid:longint; begin if l=r then begin read(tree[now]); //到叶子节点时输入信息并退出 exit; end; mid:=(l+r) shr 1; build(l,mid,now<<1); build(mid+1,r,now<<1+1); pushup(now); end; procedure update(p,add,l,r,now:longint); //更新数据 var mid:longint; begin if l=r then begin inc(tree[now],add); exit; end; mid:=(l+r) shr 1; if p<=mid then update(p,add,l,mid,now<<1) //递归求解 else update(p,add,mid+1,r,now<<1+1); pushup(now); end; function query(left,right,l,r,now:longint):longint; //询问和 var mid,ans:longint; begin if (left<=l) and (r<=right) then exit(tree[now]); mid:=(l+r) shr 1; ans:=0; if left<=mid then inc(ans,query(left,right,l,mid,now<<1)); if right>mid then inc(ans,query(left,right,mid+1,r,now<<1+1)); exit(ans); end; procedure ques(n:longint); var ch:char; a,b:longint; temp:string; begin while true do begin temp:=''; ch:='1'; while ch<>' ' do begin read(ch); temp:=temp+ch; end; delete(temp,length(temp),1); if temp='End' then exit; readln(a,b); case temp of 'Add':update(a,b,1,n,1); 'Query':writeln(query(a,b,1,n,1)); 'Sub':update(a,-b,1,n,1); end; end; end; procedure main; var i,t,n:longint; begin readln(t); for i:=1 to t do begin readln(n); build(1,n,1); readln; ques(n); end; end; begin main; end.
但是,我们如果对于区间有修改的话,这样就太慢了,O(Qnlogn),甚至比朴素算法都慢
那么,线段树的精华出现了,lazy-tag技术
Lazy-Tag 顾名思义,懒惰标记。我们每当要对一个区间进行修改时,
我们只需要访问到这个区间所包含的最大区间,然后对这个区间记一个lazy-tag
我们如此做的动机是:没有必要更新到叶子节点,而是在一个合适的范围内,上一个tag
而我们在询问的时候,每询问一个区间,查询其tag,若存在tag,则把tag下传到该区间的左儿子与右儿子,并把该区间的tag信息上传,且清空当前Tag。
这样我们能大大的增加效率。
pushdown应该如何写呢?
大概的结构是这样
if lazy[now]<>0 then
begin
do something;
end;
我们给出区间修改的问题3
维护一个数列,支持如下操作:
1.把区间[l,r]全部增加v
2.修改k点值为r
3.询问区间[l,r]的和
代码如下:(未写main函数)
//区间增减 区间求和 const maxn=600001; var lazy,tree:array [0..maxn] of longint; procedure pushup(now:longint); var left,right:longint; begin left:=now<<1; right:=left+1; tree[now]:=tree[left]+tree[right]; end; procedure pushdown(now,l,r:longint); var len,left,right,delta:longint; begin left:=now<<1; right:=left+1; delta:=lazy[now]; len:=r-l+1; if lazy[now]<>0 then begin inc(tree[now],delta*len); inc(lazy[left],delta); inc(lazy[right],delta); lazy[now]:=0; end; end; procedure build(l,r,now:longint); var mid,left,right:longint; begin mid:=(l+r)>>1; left:=now<<1; right:=left+1; lazy[now]:=0; if l=r then begin read(tree[now]); exit; end; build(l,mid,left); build(mid+1,r,right); pushup(now); end; procedure update(now,l,r:longint); var mid,left,right:longint; begin mid:=(l+r)>>1; left:=now<<1; right:=left+1; pushdown(left,l,mid); pushdown(right,mid+1,r); pushup(now); end; procedure insert(left,right,c,l,r,now:longint); var mid,leftch,rightch:longint; begin mid:=(l+r)>>1; leftch:=now<<1; rightch:=leftch+1; pushdown(now,l,r); if (left<=l) and (r<=right) then begin inc(lazy[now],c); exit; end; if left<=mid then insert(left,right,c,l,mid,leftch); if mid<right then insert(left,right,c,mid+1,r,rightch); update(now,l,r); end; function querysum(left,right,l,r,now:longint):longint; var leftch,rightch,mid,ans:longint; begin pushdown(now,l,r); if (left<=l) and (r<=right) then exit(tree[now]); mid:=(l+r) shr 1; leftch:=now<<1; rightch:=leftch+1; ans:=0; if left<=mid then inc(ans,querysum(left,right,l,mid,leftch)); if mid<right then inc(ans,querysum(left,right,mid+1,r,rightch)); exit(ans); end;
我们再升级一下问题
维护一个数列,支持如下操作:
0.询问区间[l,r]的和
1.修改单点l值为r
2.把区间[l,r]全部置为v
3.把区间[l,r]全部增加v
看上去很麻烦,我们不知道区间覆盖和区间增减的顺序的话,可能标记会出错。
但是我们只需要再维护一个sign域即可,而我们也不必在意区间覆盖和区间增减的顺序
因为:当区间覆盖与区间增量tag同时存在时,我们优先区间覆盖标记,在清空区间覆盖标记时,把区间增量标记清空
为什么呢?很显然,我们先进行区间增减,再进行区间覆盖,那么显然区间增减无意义。
但是问题来了,若我们先进行的区间覆盖,再进行区间增减,那么区间增减也会被覆盖掉,这样显然会WA.
怎么解决呢?我们在下tag时,都查询一次当前结点的tag,若当前结点存在tag,那么我们清空tag,使该层tag传递到下一层,
即当前更新不影响历史记录。
这样,我们能保持标记总是sign在上,不影响delta的传递,即覆盖标记永远优先于增量标记,且传递深度总是较增量标记传递深度大一层。
代码如下:(不支持全部覆盖为0,若要全部覆盖为0则需重新初始化sign的值)
{$inline on} const maxn=800001; var tree,sign,delta:array [0..maxn] of int64; procedure pushup(now:longint); inline; var left,right:longint; begin left:=now<<1; right:=left+1; tree[now]:=tree[left]+tree[right]; end; procedure pushdown(now,l,r:longint); inline; var left,right,len:longint; begin left:=now<<1; right:=left+1; len:=r-l+1; if sign[now]<>0 then begin sign[left]:=sign[now]; sign[right]:=sign[now]; delta[left]:=0; delta[right]:=0; tree[now]:=len*sign[now]; sign[now]:=0; end; if delta[now]<>0 then begin inc(delta[left],delta[now]); inc(delta[right],delta[now]); inc(tree[now],delta[now]*len); delta[now]:=0; end; end; procedure build(now,l,r:longint); inline; var mid,left,right:longint; begin mid:=(l+r)>>1; left:=now<<1; right:=left+1; delta[now]:=0; sign[now]:=0; if l=r then begin read(tree[now]); exit; end; build(left,l,mid); build(right,mid+1,r); pushup(now); end; procedure update(now,l,r:longint); inline; var mid,left,right:longint; begin mid:=(l+r)>>1; left:=now<<1; right:=left+1; pushdown(left,l,mid); pushdown(right,mid+1,r); pushup(now); end; procedure changepoint(pos,v,l,r,now:longint); inline; var mid,left,right:longint; begin mid:=(l+r)>>1; left:=now<<1; right:=left+1; pushdown(now,l,r); if l=r then begin tree[now]:=v; exit; end; if pos<=mid then changepoint(pos,v,l,mid,left) else changepoint(pos,v,mid+1,r,right); update(now,l,r); end; procedure change(left,right,v,l,r,now:longint); inline; var mid,leftch,rightch:longint; begin pushdown(now,l,r); mid:=(l+r)>>1; leftch:=now<<1; rightch:=leftch+1; if (left<=l) and (r<=right) then begin sign[now]:=v; delta[now]:=0; exit; end; if left<=mid then change(left,right,v,l,mid,leftch); if mid<right then change(left,right,v,mid+1,r,rightch); update(now,l,r); end; procedure insert(left,right,v,l,r,now:longint); inline; var mid,leftch,rightch:longint; begin mid:=(l+r)>>1; leftch:=now<<1; rightch:=leftch+1; pushdown(now,l,r); if (left<=l) and (r<=right) then begin inc(delta[now],v); exit; end; if left<=mid then insert(left,right,v,l,mid,leftch); if mid<right then insert(left,right,v,mid+1,r,rightch); update(now,l,r); end; function querysum(left,right,l,r,now:longint):int64; inline; var leftch,rightch,mid:longint; ans:int64; begin pushdown(now,l,r); if (left<=l) and (r<=right) then exit(tree[now]); mid:=(l+r)>>1; leftch:=now<<1; rightch:=leftch+1; ans:=0; if left<=mid then inc(ans,querysum(left,right,l,mid,leftch)); if mid<right then inc(ans,querysum(left,right,mid+1,r,rightch)); update(now,l,r); exit(ans); end; procedure swap(var l,r:longint); inline; begin l:=l xor r; r:=l xor r; l:=l xor r; end; procedure main; var i,n,m,que,l,r,a:longint; begin read(n,m); build(1,1,n); for i:=1 to m do begin read(que,l,r); if l>r then swap(l,r); case que of 0:writeln(querysum(l,r,1,n,1)); 1:changepoint(l,r,1,n,1); 2: begin read(a); change(l,r,a,1,n,1); end; 3: begin read(a); insert(l,r,a,1,n,1); end; end; end; end; begin main; end.
另外:
线段树一定要用数组,指针常数巨大。
下面是指针与数组版本的耗时比较
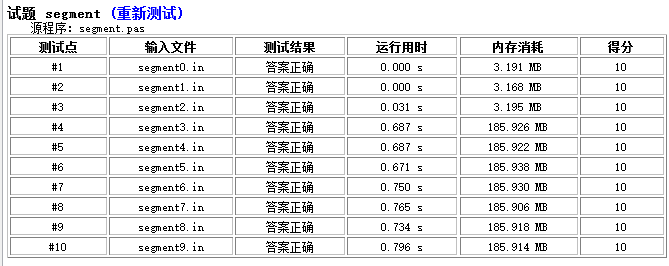
此为指针版,耗时耗空间都相当大(不排除本人蒟蒻原因写丑了)
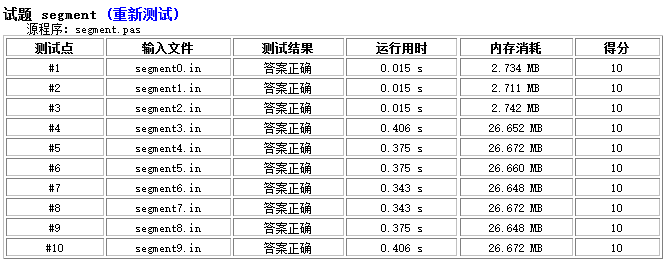
此为数组版,常数还是比较小的。