BZOJ 2819: Nim dfs序维护树状数组，倍增

1.随机选两个堆v,u，询问若在v到u间的路径上的石子堆中玩Nim游戏，是否有必胜策略，如果有，vfleaking将会考虑将这些石子堆作为初始局面之一，用来坑玩家。
2.把堆v中的石子数变为k。

 

分析：NIM游戏这有介绍。

　　题目简单描述：修改节点权值，询问路径异或和。

　　这个不就是dfs序维护树状数组吗？

　　以下借用niuox学长的一幅dfs序的图

　　

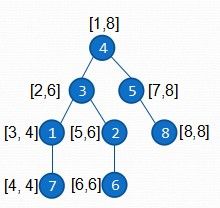
　　所以答案就是ask(st[x]) ^ ask(st[y]) ^ a[lca(x,y)] （lca(x,y)节点到根节点路径上所有的点值异或两次后值为0，所以需要异或一次lca(x,y)）。求lca直接倍增即可。

　　由于直接dfs会爆栈，所以需要手动模拟。我是无耻的打开了栈开关。。。

 

 

#pragma comment(linker, "/STACK:1024000000,1024000000")



#include <set>

#include <map>

#include <list>

#include <cmath>

#include <queue>

#include <stack>

#include <string>

#include <vector>

#include <cstdio>

#include <cstring>

#include <iostream>

#include <algorithm>



using namespace std;



typedef long long ll;

typedef unsigned long long ull;



#define debug puts("here")

#define rep(i,n) for(int i=0;i<n;i++)

#define rep1(i,n) for(int i=1;i<=n;i++)

#define REP(i,a,b) for(int i=a;i<=b;i++)

#define foreach(i,vec) for(unsigned i=0;i<vec.size();i++)

#define pb push_back

#define RD(n) scanf("%d",&n)

#define RD2(x,y) scanf("%d%d",&x,&y)

#define RD3(x,y,z) scanf("%d%d%d",&x,&y,&z)

#define RD4(x,y,z,w) scanf("%d%d%d%d",&x,&y,&z,&w)

#define All(vec) vec.begin(),vec.end()

#define MP make_pair

#define PII pair<int,int>

#define PQ priority_queue

#define cmax(x,y) x = max(x,y)

#define cmin(x,y) x = min(x,y)

#define Clear(x) memset(x,0,sizeof(x))

/*



#pragma comment(linker, "/STACK:1024000000,1024000000")



int size = 256 << 20; // 256MB

char *p = (char*)malloc(size) + size;

__asm__("movl %0, %%esp\n" :: "r"(p) );



*/



/******** program ********************/



const int MAXN = 500105;

const int LOG = 19;



int c[MAXN];

int po[MAXN],tol;

int a[MAXN];

int sta[MAXN],fa[MAXN],top;

int p[MAXN][20],dep[MAXN];

int st[MAXN],ed[MAXN],tim;

bool use[MAXN];



struct Edge{

    int y,next;

}edge[MAXN<<1];



inline void add(int x,int y){

    edge[++tol].y = y;

    edge[tol].next = po[x];

    po[x] = tol;

}



inline int lowbit(int x){

    return x & -x;

}

inline void modify(int x,int val){

    while(x<MAXN){

        c[x] ^= val;

        x += lowbit(x);

    }

}

inline int ask(int x){

    int ans = 0;

    while(x>0){

        ans ^= c[x];

        x -= lowbit(x);

    }

    return ans;

}



inline void modify(int x){

    modify(st[x],a[x]);

    modify(ed[x],a[x]);

}



void dfs(int x,int fa,int depth){

    dep[x] = depth;

    p[x][0] = fa;

    for(int i=1;i<LOG;i++)

        p[x][i] = p[ p[x][i-1] ][i-1];

    st[x] = tim++;

    for(int i=po[x];i;i=edge[i].next){

        int y = edge[i].y;

        if(y==fa)continue;

        dfs(y,x,depth+1);

    }

    ed[x] = tim;

}



inline int lca(int x,int y){ // 倍增求lca

    if(dep[x]>dep[y])swap(x,y);

    if(dep[x]<dep[y]){

        int del = dep[y]-dep[x];

        rep(i,LOG)

            if( del>>i & 1 )

                y = p[y][i];

    }

    if(x!=y){

        for(int i=LOG-1;i>=0;i--)

            if( p[x][i]!=p[y][i] ){

                x = p[x][i];

                y = p[y][i];

            }

        x = p[x][0];

        y = p[y][0];

    }

    return x;

}



int main(){



#ifndef ONLINE_JUDGE

    freopen("sum.in","r",stdin);

    //freopen("sum.out","w",stdout);

#endif



    int n,m,x,y;

    char op[2];

    while(~RD(n)){

        rep1(i,n)

            RD(a[i]);

        Clear(po);

        tol = 0;

        REP(i,2,n){

            RD2(x,y);

            add(x,y);

            add(y,x);

        }



        tim = 1;

        dfs(1,1,1);

        rep1(i,n)

            modify(i);



        RD(m);

        while(m--){

            scanf("%s%d%d",op,&x,&y);

            if(op[0]=='Q'){

                if(ask(st[x])^ask(st[y])^a[lca(x,y)])

                    puts("Yes");

                else

                    puts("No");

            }else{

                modify(x);

                a[x] = y;

                modify(x);

            }

        }

    }



    return 0;

}