哈夫曼树与哈夫曼编码

在一般的数据结构的书中，树的那章后面，著者一般都会介绍一下哈夫曼(HUFFMAN)

树和哈夫曼编码。哈夫曼编码是哈夫曼树的一个应用。哈夫曼编码应用广泛，如

JPEG中就应用了哈夫曼编码。 首先介绍什么是哈夫曼树。哈夫曼树又称最优二叉树，

是一种带权路径长度最短的二叉树。所谓树的带权路径长度，就是树中所有的叶结点

的权值乘上其到根结点的 路径长度（若根结点为0层，叶结点到根结点的路径长度

为叶结点的层数）。树的带权路径长度记为WPL= (W1*L1+W2*L2+W3*L3+...+Wn*Ln)

，N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树，相应的叶结点的路径

长度为Li(i=1,2,...n)。可以证明哈夫曼树的WPL是最小的。

哈夫曼编码步骤：

一、对给定的n个权值{W1,W2,W3,...,Wi,...,Wn}构成n棵二叉树的初始集合F= {T1,T2,T3,...,Ti,...,Tn}，其中每棵二叉树Ti中只有一个权值为Wi的根结点，它的左右子树均为空。（为方便在计算机上实现算 法，一般还要求以Ti的权值Wi的升序排列。）
二、在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树，新二叉树的根结点的权值为其左右子树的根结点的权值之和。
三、从F中删除这两棵树，并把这棵新的二叉树同样以升序排列加入到集合F中。
四、重复二和三两步，直到集合F中只有一棵二叉树为止。

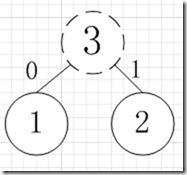
简易的理解就是，假如我有A,B,C,D,E五个字符，出现的频率（即权值）分别为5,4,3,2,1,那么我们第一步先取两个最小权值作为左右子树构造一个新树，即取1，2构成新树，其结点为1+2=3，如图：

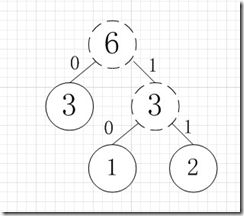
虚线为新生成的结点，第二步再把新生成的权值为3的结点放到剩下的集合中，所以集合变成{5,4,3,3}，再根据第二步，取最小的两个权值构成新树，如图：

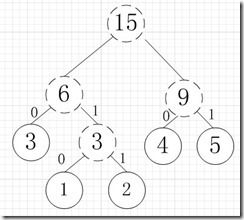
再依次建立哈夫曼树，如下图：

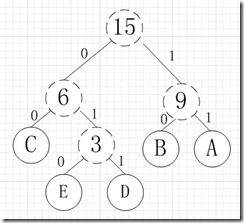
其中各个权值替换对应的字符即为下图：

所以各字符对应的编码为：A->11,B->10,C->00,D->011,E->010

霍夫曼编码是一种无前缀编码。解码时不会混淆。其主要应用在数据压缩，加密解密等场合。

 

C语言代码实现：

  1 /*-------------------------------------------------------------------------

  2  * Name:   哈夫曼编码源代码。

  3  * Date:   2011.04.16

  4  * Author: Jeffrey Hill+Jezze(解码部分)

  5  * 在 Win-TC 下测试通过

  6  * 实现过程：着先通过 HuffmanTree() 函数构造哈夫曼树，然后在主函数 main()中

  7  *           自底向上开始(也就是从数组序号为零的结点开始)向上层层判断，若在

  8  *           父结点左侧，则置码为 0,若在右侧,则置码为 1。最后输出生成的编码。

  9  *------------------------------------------------------------------------*/

 10 #include <stdio.h>

 11 #include<stdlib.h>

 12  

 13 #define MAXBIT      100

 14 #define MAXVALUE  10000

 15 #define MAXLEAF     30

 16 #define MAXNODE    MAXLEAF*2 -1

 17  

 18 typedef struct 

 19 {

 20     int bit[MAXBIT];

 21     int start;

 22 } HCodeType;        /* 编码结构体 */

 23 typedef struct

 24 {

 25     int weight;

 26     int parent;

 27     int lchild;

 28     int rchild;

 29     int value;

 30 } HNodeType;        /* 结点结构体 */

 31  

 32 /* 构造一颗哈夫曼树 */

 33 void HuffmanTree (HNodeType HuffNode[MAXNODE],  int n)

 34 { 

 35     /* i、j： 循环变量，m1、m2：构造哈夫曼树不同过程中两个最小权值结点的权值，

 36         x1、x2：构造哈夫曼树不同过程中两个最小权值结点在数组中的序号。*/

 37     int i, j, m1, m2, x1, x2;

 38     /* 初始化存放哈夫曼树数组 HuffNode[] 中的结点 */

 39     for (i=0; i<2*n-1; i++)

 40     {

 41         HuffNode[i].weight = 0;//权值 

 42         HuffNode[i].parent =-1;

 43         HuffNode[i].lchild =-1;

 44         HuffNode[i].rchild =-1;

 45         HuffNode[i].value=i; //实际值，可根据情况替换为字母  

 46     } /* end for */

 47  

 48     /* 输入 n 个叶子结点的权值 */

 49     for (i=0; i<n; i++)

 50     {

 51         printf ("Please input weight of leaf node %d: \n", i);

 52         scanf ("%d", &HuffNode[i].weight);

 53     } /* end for */

 54  

 55     /* 循环构造 Huffman 树 */

 56     for (i=0; i<n-1; i++)

 57     {

 58         m1=m2=MAXVALUE;     /* m1、m2中存放两个无父结点且结点权值最小的两个结点 */

 59         x1=x2=0;

 60         /* 找出所有结点中权值最小、无父结点的两个结点，并合并之为一颗二叉树 */

 61         for (j=0; j<n+i; j++)

 62         {

 63             if (HuffNode[j].weight < m1 && HuffNode[j].parent==-1)

 64             {

 65                 m2=m1; 

 66                 x2=x1; 

 67                 m1=HuffNode[j].weight;

 68                 x1=j;

 69             }

 70             else if (HuffNode[j].weight < m2 && HuffNode[j].parent==-1)

 71             {

 72                 m2=HuffNode[j].weight;

 73                 x2=j;

 74             }

 75         } /* end for */

 76             /* 设置找到的两个子结点 x1、x2 的父结点信息 */

 77         HuffNode[x1].parent  = n+i;

 78         HuffNode[x2].parent  = n+i;

 79         HuffNode[n+i].weight = HuffNode[x1].weight + HuffNode[x2].weight;

 80         HuffNode[n+i].lchild = x1;

 81         HuffNode[n+i].rchild = x2;

 82  

 83         printf ("x1.weight and x2.weight in round %d: %d, %d\n", i+1, HuffNode[x1].weight, HuffNode[x2].weight);  /* 用于测试 */

 84         printf ("\n");

 85     } /* end for */

 86   /*  for(i=0;i<n+2;i++)

 87     {

 88         printf(" Parents:%d,lchild:%d,rchild:%d,value:%d,weight:%d\n",HuffNode[i].parent,HuffNode[i].lchild,HuffNode[i].rchild,HuffNode[i].value,HuffNode[i].weight);

 89                   }*///测试 

 90 } /* end HuffmanTree */

 91  

 92 //解码 

 93 void decodeing(char string[],HNodeType Buf[],int Num)

 94 {

 95   int i,tmp=0,code[1024];

 96   int m=2*Num-1;

 97   char *nump;

 98   char num[1024];

 99   for(i=0;i<strlen(string);i++)

100   {

101    if(string[i]=='0')

102   num[i]=0;        

103   else

104   num[i]=1;                    

105   } 

106   i=0;

107   nump=&num[0];

108   

109  while(nump<(&num[strlen(string)]))

110  {tmp=m-1;

111   while((Buf[tmp].lchild!=-1)&&(Buf[tmp].rchild!=-1))

112   {

113   

114    if(*nump==0)

115    {

116      tmp=Buf[tmp].lchild ;          

117    } 

118    else tmp=Buf[tmp].rchild;

119    nump++;

120         

121   } 

122   

123   printf("%d",Buf[tmp].value);                                  

124  }

125  

126   

127 }

128  

129  

130 int main(void)

131 {

132     

133     HNodeType HuffNode[MAXNODE];            /* 定义一个结点结构体数组 */

134     HCodeType HuffCode[MAXLEAF],  cd;       /* 定义一个编码结构体数组， 同时定义一个临时变量来存放求解编码时的信息 */

135     int i, j, c, p, n;

136     char pp[100];

137     printf ("Please input n:\n");

138     scanf ("%d", &n);

139     HuffmanTree (HuffNode, n);

140    

141     

142     for (i=0; i < n; i++)

143     {

144         cd.start = n-1;

145         c = i;

146         p = HuffNode[c].parent;

147         while (p != -1)   /* 父结点存在 */

148         {

149             if (HuffNode[p].lchild == c)

150                 cd.bit[cd.start] = 0;

151             else

152                 cd.bit[cd.start] = 1;

153             cd.start--;        /* 求编码的低一位 */

154             c=p;                    

155             p=HuffNode[c].parent;    /* 设置下一循环条件 */

156         } /* end while */

157         

158         /* 保存求出的每个叶结点的哈夫曼编码和编码的起始位 */

159         for (j=cd.start+1; j<n; j++)

160         { HuffCode[i].bit[j] = cd.bit[j];}

161         HuffCode[i].start = cd.start;

162     } /* end for */

163     

164     /* 输出已保存好的所有存在编码的哈夫曼编码 */

165     for (i=0; i<n; i++)

166     {

167         printf ("%d 's Huffman code is: ", i);

168         for (j=HuffCode[i].start+1; j < n; j++)

169         {

170             printf ("%d", HuffCode[i].bit[j]);

171         }

172         printf(" start:%d",HuffCode[i].start);

173        

174         printf ("\n");

175         

176     }

177 /*    for(i=0;i<n;i++){

178     for(j=0;j<n;j++)

179         {

180              printf ("%d", HuffCode[i].bit[j]);           

181         }

182         printf("\n");

183         }*/

184     printf("Decoding?Please Enter code:\n");

185     scanf("%s",&pp);

186 decodeing(pp,HuffNode,n);

187     getch();

188     return 0;

189 }

hehe

 

转载自 http://www.cnblogs.com/Jezze/archive/2011/12/23/2299884.html