哈希表

 效率　　　　　　　　　　　　　　　　　　　　　　　 插入删除

哈希表	O[1]
树	O[N]
链表	O[1]
有序数组	O[N]

缺点

基于数组.难于扩展.被填满时候效率低下.无法有序遍历.

 

哈希化：

一种压缩方法把数位幂的连乘系统中得到的巨大的整数范围压缩到

可接受的数组范围中。

samllNumber = largetNumber%smallRange;

这就是一种哈希函数:把一个大范围的数字哈希成一个小范围的数字.

这个小的范围对应着数组的下标.

arrayIndex = hugeNumber%arraySize;

然后使用取余操作符.把得到的巨大的整数范围转换成两倍于要储存内容的数组下标范围：

arraySize = numberWords*2;

arrayIndex = hugeNumber%arraySize;

 

 

哈希表：

使用哈希函数向数组插入数据后.这个数组就称为哈希表.

例子：

想在内存中存储50000个单词.起初可能考虑每个单词占据一个数组单元.那么数组大小50000.

同时可以使用数组下标存取单词.这样存取确实很快.

单词转换成数组下标:

*数字累加法

一个转换单词的简单方法是把单词每一个字符代码求和.

例如把单词cats转换成数字.

c=3

a=1

t=20

s=19

然后把它们相加：3+1+20+19=43.那么在字典表中.单词cats存储在数组下标为43的

单元中.所有的英文单词都用这个办法转换成数组下标.

哈希函数.把一个大范围的数字数字哈希转化成一个小范围的数字.这个小范围的数字对应着数组的下标.

arrayIndex = hugeNumber%arraySize;

*幂连乘<----确保单词中的每个字符都可以通过独一无二的方法得到最终的数字.

回忆一下：把单词每个字母乘以27的适当次幂.使单词成为一个巨大的数字.

 

 

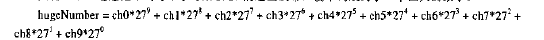
数字折叠：

 

冲突:

把巨大的数字空间压缩成较小的数字空间.必然要付出代价.不能保证每个单词映射到数组的空白单元.

解决冲突:

开放地址法：

通过系统的方法找到数组的一个空位.把这个单词填入.

而不再用哈西函数的到数组的下标.

 *线形探测：线性查找空白单元.

find()

//find item with key

public DataItem find(int key){

//assums table not full

//hash the key

int hashVal = hashFunc(key);

//until empty cell

while(hashArray[hashVal]!=null){

       if(hashArray[hashVal].getKey()==key)

                     return hashArray[hashVal];  

  

        ++hashVal;
      //wrap around if nessary

         hashVal %=arraySize;

}

       return null;

}

 

//in this method i myself wanna insert a new item into the

//assumes table not full

public void insert(DataItem item)(

   //extract key

     int key = item.getKey();

  //hash the key

//until empty cell or -1

     int hashVal = hashFunc(key);



//find the propur index for the new item

     while(hashArray[hashVal]!=null &&

           hashArray[hashVal].iData!=-1

      ){

         ++hashVal;

         hashVal%=   arraySize;

       }

        hashArray[hashVal]=item;

}       

 

//delete dedecate  data item

public DataItem delete(int key){

//i got the dedecate data from the key

               int hashVal =  

            hashFunc[key];

//until the empty cell

//found the key

        while(hashArray[hashVal]!=null){

                if(hashArray[hashVal].getKey()==key){

                               DateItem temp = //save item

                                  hashArray[hashVal];

                             //leave it to empty cell

                              hashArray[hashVal] = nonItem;

                              return temp;

                }

         ++hashVal;

         hashVal %= arrraySize;

       }

}

 

 *二次探测

在线形探测中.哈希函数原始下标 x.线形探测是x+1.x+2.x+3

二次探测:x+1.x+4.x+9.x+16.x+25.

当二次探测的搜索变长时候.好像它变得越来越绝望.第一次.它查找相邻的单元.

如果这个单元被占用.它认为这里可能是一个小的聚集.所以它尝试距离为4的单元.

如果这里也被占用.它变得焦虑.认为这里有一个更大的聚集.然后它尝试距离为9的单元.

如果这里还被占用.它感到一丝恐慌.跳到距离为16的单元.很快它会歇斯底里的飞跃整个数组空间.

当哈希表几乎填满时候.就会出现这种情况.

 

二次探测的问题：

二次探测消除了在线形探测中产生的聚集问题.这种聚集叫原始聚集.然而二次探测产生了另一种.更细的聚集问题.

二次聚集.比如将184.302.420.544依次插入到表中.他们都影射到7.那么302需要以一为步长的探测.

420需要以4为步长的探测.544需要以9为步长的探测.只要一有项.其关键字影射到7.就需要更长步长的探测.

这种现象叫做二次聚集.

 

 

 *再哈希法

stepSize = constant -(key%constant);
constant是质数且小于数组容量
stepSize = 5-(key%5);

现在需要一种方法是产生一种依赖关键字的探测序列.而不是每个关键字都一样.

对于指定的关键字.步长在整个探测中是不变的.不过不同的关键字使用不同的步长.

表的容量是一个质数:

再哈西法要求表的容量是一个质数.

假设表的容量不是质数.例如假设表长是15<下标从0到14>

有一个特定关键字映射到0.步长为5.探测序列是0.

5 10 0 5 10 依次类推.一直循环.算法只尝试这三个单元.

所以不能找到某些空白单元.

例如位置1，2，3或者其他位置.算法会最终导致崩溃.

链地址法:在哈西标的每个单元中设置链表  

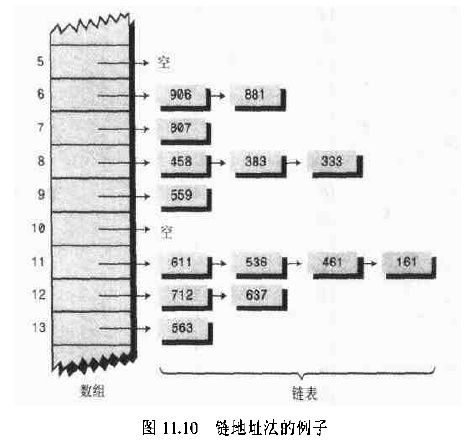
效率：

查找/插入: 1+nComps -->nComps关键字比较次数