ZOJ 3723 (浙大月赛)状压DP

A了一整天~~~终于搞掉了。

真是血都A出来了。

题目意思很清楚，肯定是状压DP。

我们可以联系一下POJ 1185  炮兵阵地，经典的状压DP。

两道题的区别就在于，这道题的攻击是可以被X挡住的，而且攻击的范围不同。

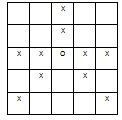这是这道题的攻击范围。

但是这个攻击范围是会被X挡住的。

所以得在1185上加以改进。

分析：

POJ 1185，因为可以隔着障碍物打，所以他每行的状态是一样的，但是这题由于攻击会被挡住，所以每行的状态是不一样的，所以我们预处理的时候就要处理出每一行的状态数，分别保存，然后存下每行每个状态的数量。

因为我的下标是从0开始的，所以我得预先处理一下第0行和第1行的状态转移过程，这个很好处理，具体看代码。

那么预处理完毕之后就是状态转移的过程。

变量定义：

M[i] ：每一行的地图压缩。

st[i][j] ：第j行，第i个状态。

Count[i][j] ：第j行第i个状态的数量。

num[i]：第i 行状态的总数。

dp[i][j][k] ：第i行的状态是k ,第i - 1 行的状态是j的可行状态总数。

这道题貌似还卡内存，必须使用滚动数组，因为状压的时候他只需要3个状态，所以这里i开到3就可以了。

状态转移的过程，首先当前状态是k ,上一状态是j，上上状态是l 。

那么首先判断k 和 j的状态可行性，首先j不能出现在k的上方，那就是(st[j][i - 1] & st[k][i]) ，然后k 也不能出现在j的左下和右下的位置，通过上图可以看出，k不能出现在j的左移一位，右移一位的位置。那么可以这么判断(st[j][i - 1] >> 1 & st[k][i]), (st[j][i - 1] << 1 & st[k][i]) 。这样就处理完j 和k 这两个状态了。

接下来是j和l，这里的判断同j和k，因为都是相邻的两行，这里不多说了，一样的，下面着重讲一下l和k的状态的判断。

因为l和k之间是可能隔着X的，所以我们不能直接判断，而应该判断他们之间是否有X。

比如判断l是否在k上方，那么不能直接(st[l][i - 2] & st[k][i])，因为他们之间如果有X，那么该状态是成立的。

那么到底如何判断呢。昨天我也是在这里卡住了，今天早上突然想到，其实我们只要判断l状态和k状态都是1的位置，那么他们的i - 1行该位置是否是X就行了。而判断X我们可以直接使用压缩过的地图进行判断。

那么可以这样：

int s = (st[l][i - 1] & st[k][i]) ;

if(s & M[i - 1] != s)

那么就证明他们之间是会互相攻击的，s & (M[i -1] ) != s，就说明l和k都为1的位置他们中间至少有一处不为X，那么该状态不可行。

同理我们可以判断 l状态的左下攻击和右下攻击是否会打到k状态。

如果是左下攻击，那么只需要将l状态左移两位与k判断，然后判断他们的之间是否有X。具体看代码，我就不多解释了，相信自己动手画张图还是很好理解的。

同理右下攻击。

至于为什么相邻两列之间的左下攻击右下攻击不需要判断X，相信大家想一下都能想到。

下面贴代码。

 

#include <set>

#include <map>

#include <stack>

#include <cmath>

#include <queue>

#include <cstdio>

#include <string>

#include <vector>

#include <iomanip>

#include <cstring>

#include <iostream>

#include <algorithm>

#define Max 2505

#define ll long long

#define PI acos(-1.0)

#define inf 0x7fffffff

#define LL(x) ( x << 1 )

#define bug puts("here")

#define PII pair<int,int>

#define RR(x) ( x << 1 | 1 )

#define mp(a,b) make_pair(a,b)

#define mem(a,b) memset(a,b,sizeof(a))

#define REP(i,s,t) for( int i = ( s ) ; i <= ( t ) ; ++ i )



using namespace std;



inline void RD(int &ret) {

    char c;

    do {

        c = getchar();

    } while(c < '0' || c > '9') ;

    ret = c - '0';

    while((c=getchar()) >= '0' && c <= '9')

        ret = ret * 10 + ( c - '0' );

}



inline void OT(int a) {

    if(a >= 10)OT(a / 10) ;

    putchar(a % 10 + '0') ;

}

#define N 190

int n , m ;

char Map[1001][15] ;

int M[1001] ;

int st[N][1001] ;

int top ;

int Count[N][1001] ;

int num[1001] ;

//int dp[1111][N][N] ;

int dp[3][N][N] ;

void init() {

    mem(M ,0) ;

    mem(st ,0) ;

    top = 0 ;

    mem(Count ,0) ;

    mem(dp ,0) ;

    mem(num ,0) ;

}



void ok() {

    for (int i = 0 ; i < n ; i ++ ) {

        for (int j = 0 ; j < 1 << m ; j ++ ) {

            int d = 0 ;

            bool flag = 0 ;

            for (int k = 0 ; k < m ; k ++ ) {

                if(j & (1 << k)) {

                    if(Map[i][k] == 'X') {

                        flag = 1 ;

                        break ;

                    }

                    if(d > 2) {

                        flag = 1 ;

                        break ;

                    }

                    d = 4 ;

                } else {

                    if(Map[i][k] == 'X') {

                        d = 0 ;

                        continue ;

                    }

                    d -- ;

                }

            }

            if(flag)continue ;



            int tt = j ;

            int nn = 0 ;

            while(tt) {

                nn += tt % 2 ;

                tt /= 2 ;

            }

//            cout << j << endl;

            st[num[i]][i] = j ;

            Count[num[i] ++ ][i] = nn ;

        }

    }

}

int main() {



    while(cin >> n >> m , ( n + m )) {

        init() ;

        for (int i = 0 ; i < n ; i ++ ) {

            scanf("%s",Map[i]) ;

            for (int j = 0 ; j < m ; j ++ ) {

                if(Map[i][j] == 'X')M[i] += (1 << j) ;

            }

//            cout << M[i] << endl;

        }

        ok() ;



        int ans = 0 ;

        //预处理第0行

        for (int i = 0 ; i < num[0] ; i ++ ) {

            if(st[i][0] & M[0])continue ;

            dp[0][0][i] = Count[i][0] ;

            ans = max(ans ,dp[0][0][i]) ;

        }

        //预处理第1行

        for (int i = 0 ; i < num[1] ; i ++ ){

            if(st[i][1] & M[1])continue ;

            for (int j = 0 ; j < num[0] ; j ++ ){

                if(st[j][0] & st[i][1])continue ;

                if(st[j][0] >> 1 & st[i][1])continue ;

                if(st[j][0] << 1 & st[i][1])continue ;

                dp[1][j][i] = max(dp[1][j][i] , dp[0][0][j] + Count[i][1]) ;

            }

        }



        //状态转移过程

        for (int i = 2 ; i < n ; i ++ ) {

            for (int j = 0 ; j < num[i - 1]  ; j ++ ) {

                for (int k = 0 ; k < num[i]  ; k ++ ) {

                    if((M[i] & st[k][i])|| (M[i - 1] & st[j][i - 1]) ||

                       ((st[j][i - 1] << 1) & st[k][i]) || ((st[j][i - 1] >> 1) & st[k][i]))continue ;

                    if(st[j][i - 1] & st[k][i])continue ;

                    for (int l = 0 ; l < num[i - 2]  ; l ++ ) {

                        if((M[i - 2] & st[l][i - 2] )|| (st[l][i - 2] & st[j][i - 1])) continue ;

                        if(((st[l][i - 2] >> 1) & st[j][i - 1]) || ((st[l][i - 2] << 1) & st[j][i - 1]))continue ;

                        if(!dp[(i + 2) % 3][l][j]) continue ;

                        int s = (st[l][i - 2] >> 2 ) & st[k][i] ;//右下

                        if(s) {

                            s <<= 1 ;

                            if((s & M[i - 1]) != s)continue ;

                        }

                        s = (st[l][i - 2] << 2 ) & st[k][i] ;//左下

                        if(s) {

                            s >>= 1 ;

                            if((s & M[i - 1]) != s)continue ;

                        }

                        s = (st[l][i - 2]) & st[k][i] ;//上方

                        if(s){

                            if((s & M[i - 1]) != s)continue ;

                        }

                        dp[i % 3][j][k] = max(dp[i % 3][j][k] , dp[(i + 2) % 3][l][j] + Count[k][i]) ;

                        ans = max(ans ,dp[i % 3][j][k]) ;

//                        bug ;



                    }

                }

            }

        }

        cout << ans << endl ;

    }

    return 0 ;

}