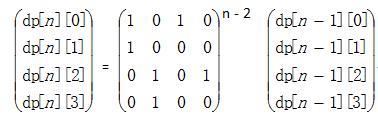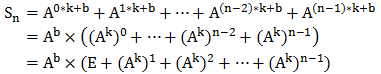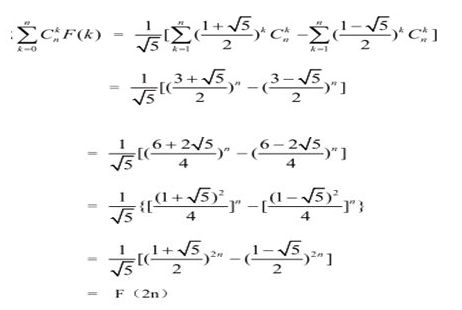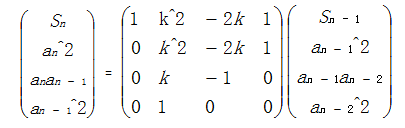【矩阵乘法专题】解题报告
HDU 1575 Tr A
水题。直接矩阵快速幂后求对角线元素和。
HDU 1757 A Simple Math Problem
水题。公式非常容易推。
HDU 2604 Queuing
以mm结尾的只能由fm结尾的或者mm结尾的推来。以mf结尾的只能由mm结尾的推来,以fm结尾的只能由mf或者ff推来,以ff结尾的只能由mf推来。于是定义状态dp[i][j] 表示i位数以j状态结尾的数的个数。j=0,1,2,3分别表示以mm,mf,fm,ff结尾。
于是可以得到dp方程:
dp[i][0]=dp[i-1][2] + dp[i-1][0]
dp[i][1]=dp[i-1][0]
dp[i][2]=dp[i-1][1] + dp[i-1][3]
dp[i][3]=dp[i-1][1]
这样之后搞出系数矩阵就是了:
dp[n][0]+dp[n][1]+dp[n][2]+dp[n][3]就是答案了。
HDU 1588 Gauss Fibonacci
题目也不难,提提公因式矩阵就出来了。然后分别做两次快速幂,一次是Fibonacci矩阵的,一次是求和的。
HDU 3117 Fibonacci Numbers
后四位可以用矩阵快速幂求出来,前面四位数是用一条公式计算出来的,这条公式是这样子的:
貌似这条公式经常遇到啊,后面还有一题要用到这公式。
HDU 2254 奥运
这道题一看之下是不会做的,但不失为一道经典题目。下面简单介绍这个经典解法:
给定一个有向图,问从A点恰好走k步(允许重复经过边)到达B点的方案数mod p的值
把给定的图转为邻接矩阵,即A(i,j)=1当且仅当存在一条边i->j。令C=A*A,那么C(i,j)=ΣA(i,k)*A(k,j),实际上就等于从点i到点j恰好经过2条边的路径数(枚举k为中转点)。类似地,C*A的第i行第j列就表示从i到j经过3条边的路径数。同理,如果要求经过k步的路径数,我们只需要二分求出A^k即可。
在此转载Matrix67的一篇不错的博文《十个利用矩阵乘法解决的经典题目》
HDU 2276 Kiki & Little Kiki 2
看到这么大的数据规模,想到要用矩阵做的,但是又不敢相信,唉~,题目隐藏得太深了。
当某个位的左边是1时该位0 -> 1,1 -> 0,左边是0时该位0->0,1->1,不难发现当考虑线性结构的话有f[i] = (f[i] + f[i-1]) % 2。题目是环形的,自己处理一下边界就行了,那么矩阵是这样子的(n = 10):
HDU 2855 Fibonacci Check-up
这道题的组合数很难办,那么我们的目的是要利用Fibonacci数消化掉那么庞大的组合数C(n,k),否则就没法求了。这样我们转化一下:
最后竟然是F(2n)你敢信?!
HDU 2971 Tower
Sn = Sn-1 + an2;
an = 2*a2*an-1-an-2;
令k = 2*a2那么 Sn = Sn-1 + (2*a2*an-1-an-2)2 = Sn-1 + k2*an-12 - 2*k*an-1-an-2 + an-22;
然后构造出矩阵为:
注意负数要加MOD变正。
HDU 2294 Pendant
非常好的一道题,DP+矩阵优化。
首先,容易得到DP转移方程:
dp[i][j]表示长度为i的pendant,用了j种珍珠,所构成的方案数, 则dp[i][j] = dp[i-1][j] * j + dp[i-1][j-1] * (k-j+1)
那么dp[1][k]+dp[2][k]+…+dp[n][k]为所求。
构造矩阵为:
初始化dp[0][0] = 1, dp[0][i] = 0 (1<=i<=k);
这样之后快速幂求和即可。