《大话数据结构》第9章 排序 9.8 归并排序（下）

9.8.3 归并排序复杂度分析
        我们来分析一下归并排序的时间复杂度，一趟归并需要将SR[1]～SR[n]中相邻的长度为h的有序序列进行两两归并。并将结果放到TR1[1]～TR1[n]中，这需要将待排序序列中的所有记录扫描一遍，因此耗费O(n)时间，而由完全二叉树的深度可知，整个归并排序需要进行⌈log₂n⌉趟，因此，总的时间复杂度为O(nlogn)，而且这是归并排序算法中最好、最坏、平均的时间性能。
        由于归并排序在归并过程中需要与原始记录序列同样数量的存储空间存放归并结果以及递归时深度为log2n的栈空间，因此空间复杂度为O(n+logn)。
        另外，对代码进行仔细研究，发现Merge函数中有if (SR[i]<SR[j])语句，这就说明它需要两两比较，不存在跳跃，因此归并排序是一种稳定的排序算法。
        也就是说，归并排序是一种比较占用内存，但却效率高且稳定的算法。

9.8.4 非递归实现归并排序
        我们常说，“没有最好，只有更好。”归并排序大量引用了递归，尽管在代码上比较清晰，容易理解，但这会造成时间和空间上的性能损耗。我们排序追求的就是效率，有没有可能将递归转化成迭代呢？结论当然是可以的，而且改动之后，性能上进一步提高了。来看代码。

/*  对顺序表L作归并非递归排序  */
  1   void  MergeSort2(SqList  * L)
  2  {
  3    int *  TR = ( int * )malloc(L -> length  *   sizeof ( int ));  /*  申请额外空间  */
  4    int  k = 1 ;
  5    while (k < L -> length)
  6   {
  7    MergePass(L -> r,TR,k,L -> length);
  8    k = 2 * k;         /*  子序列长度加倍  */
  9    MergePass(TR,L -> r,k,L -> length);
  10    k = 2 * k;         /*  子序列长度加倍  */        
 11   }
  12  }
 

1) 程序开始执行，数组L为{50,10,90,30,70,40,80,60,20}，L.length=9。
2) 第3行，我们事先申请了额外的数组内存空间，用来存放归并结果。
3) 第5～11行，是一个while循环，目的就不断的归并有序序列。注意k值的变化，第8行与第10行，在不断循环中，它将由1→2→4→8→16，跳出循环。
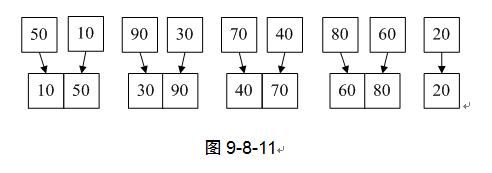
4) 第7行，此时k=1，MergePass函数将原来的无序数组两两归并入TR，此函数代码稍后再讲。如图9-8-11。
 

5) 第8行，k=2
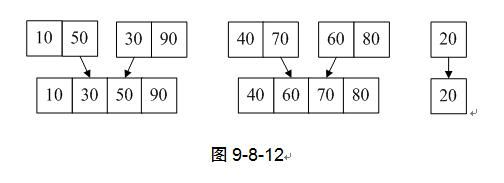
6) 第9行，MergePass函数将TR中已经两两归并的有序序列再次归并回数组L.r中，如图9-8-12。
 

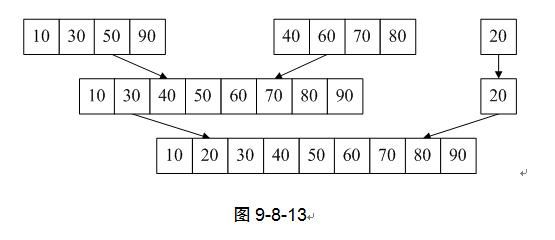
7) 第10行，k=4，因为k<9，所以继续循环，再次归并，最终执行完第7～10行，k=16，结束循环，完成排序工作。如图9-8-13。
 

        从代码中，我们能够感受到，非递归的迭代做法更加直截了当，从最小的序列开始归并直至完成。不需要像归并的递归算法一样，需要先拆分递归，再归并退出递归。
        现在我们来看MergePass代码是如何实现的。

 

/*  将SR[]中相邻长度为s的子序列两两归并到TR[]  */
  1   void  MergePass( int  SR[], int  TR[], int  s, int  n)
  2  {
  3    int  i = 1 ;
  4    int  j;
  5    while (i  <=  n - 2 * s + 1 ) 
 6   { 
 7    Merge(SR,TR,i,i + s - 1 ,i + 2 * s - 1 );  /*  两两归并  */
  8    i = i + 2 * s;        
 9   }
  10    if (i < n - s + 1 )   /*  归并最后两个序列  */
  11    Merge(SR,TR,i,i + s - 1 ,n);
  12    else     /*  若最后只剩下单个子序列  */
  13     for (j  = i;j  <=  n;j ++ )
  14     TR[j]  =  SR[j];
  15  }
 

1) 程序执行。我们第一次调用“MergePass(L.r,TR,k,L.length);”，此时L.r是初始无序状态，TR为新申请的空数组，k=1，L.length=9。
2) 第5～9行，循环的目的就两两归并，因s=1，n-2*s+1=8，为什么循环i从1到8，而不是9呢？就是因为两两归并，最终9条记录定会剩下来，无法归并。
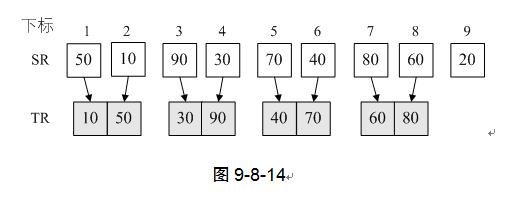
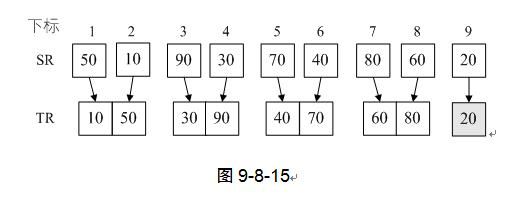
3) 第7行，Merge函数我们前面已经详细讲过，此时i=1，i+s-1=1，i+2*s-1=2。也就是说，我们将SR（即L.r）中的第一个和第二个记录归并到TR中。然后第8行，i=i+2*s=3，再循环，我们就是将第三个和第四个记录归并到TR中，一直到第七和第八个记录完成归并。如图9-8-14。
 

4) 第10～14行，主要是处理最后的尾数的，第11行是说将最后剩下的多个记录归并到TR中。不过由于i=9，n-s+1=9，因此执行第13～14行，将20放入到TR数组的最后。
 

 

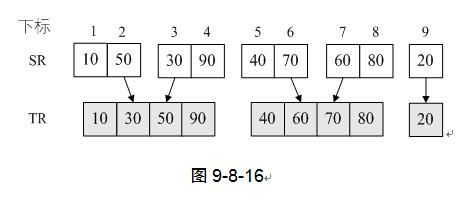
5) 再次调用MergePass时，s=2，第5～9行的循环，由第8行的i=i+2*s可知，此时i就是以4为增量进行循环了。也就是说，是将两个有两个记录的有序序列进行归并为四个记录的有序序列。最终再将最后剩下的第九条记录“20”插入TR。
 

6) 后面的类似，略。
        非递归的迭代方法，避免了递归时深度为log ₂n的栈空间，空间只是用到申请归并临时用的TR数组，因此空间复杂度为O(n)。并且避免递归也在时间性能上有一定的提升，应该说，使用归并排序时，尽量考虑用非递归方法。