0. 全文索引的核心就是倒排索引.
1. 若数字不支持范围查询, 直接变成字符串查找即可
2. 如果要支持范围查询, 直接的字符串存储支持么?
目前lucene要求term按照字典序(lexicographic sortable)排列,然后它的范围查询根据tii找到范围的起始Term,然后把这中间的所有的Term展开成一个BooleanQuery。
因此, 若按照现有的方式, 如果直接保存16,24,3,46, 当搜索[24,46]的时候, 会同时将3也搜索出来, 这是有问题的.
为了解决这个问题,初步想到的方案有:
(1) 数字能够补齐成固定的位数, 例如上面这个例子, 固定是两位, 补齐后的结果是:
03,16,24,46, 当搜索[24,46]的时候, 就正确了.
(2) 建索引的时候, term的排序按照数字来排序, 上面的例子, 顺序是3,16,24,46, 搜索的时候也会正确.
上面的方案有的问题是:
(1) 方案1固定多少位是个问题, 固定补齐的位数太多, 浪费空间; 太少, 则存储的值的范围有限
(2) 方案1和方案2都存在的问题, 展开成所有的Term的BooleanOr的query有一个问题,那就是如果范围太大,那么可能包含非常多的Boolean Clause,较早的版本可能会抛出Too Many Boolean Clause的Exception。后来的版本做了改进,不展开所以的term,而是直接合并这些term的倒排表。这样的缺点是合并后的term的算分成了问题,比如tf,你是把所有的term的tf加起来算一个term,idf呢,coord呢?(lucene的Scoring也会在后面讲到,可以参考http://lucene.apache.org/core/old_versioned_docs/versions/3_5_0/api/core/org/apache/lucene/search/Similarity.html和http://lucene.apache.org/core/old_versioned_docs/versions/3_5_0/scoring.html)
即使我们可以合并成一个term,合并这些term的docIds也是很费时间的,因为这些信息都在磁盘上。
3. lucene数字范围搜索的解决方案
首先可以把数值转换成一个字符串,并且保持顺序。也就是说如果 number1 < number2 ,那么transform(number) < transform(number)。transform就是把数值转成字符串的函数,如果拿数学术语来说,transform就是单调的。
注意, 数字做索引时, 只能是同一类型, 例如不可能是同一个field, 里面有int, 又有float的.
3.1 首先float可以转成int,double可以转成long,并且保持顺序。
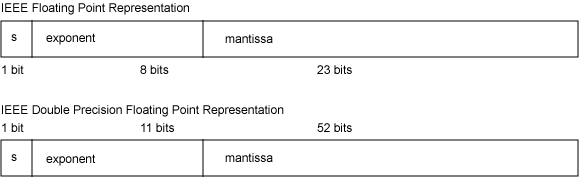
这个是不难实现的,因为float和int都是4个字节,double和long都是8个字节,从概念上讲,如果是用科学计数法,把指数放在前面就行了,因为指数大的肯定大,指数相同的尾数大的排前面。 比如 0.5e3, 0.4e3, 0.2e4,那么逻辑上保存的就是<4, 0.2> <3, 0.5> <3, 0.4>,那么显然是保持顺序的。Java的浮点数采用了ieee 754的表示方法(参考http://docs.oracle.com/javase/6/docs/api/java/lang/Float.html#floatToIntBits(float)),它的指数在前,尾数在后,第 31 位(掩码 0x80000000 选定的位)表示浮点数的符号。第 30-23 位(掩码 0x7f800000 选定的位)表示指数。第 22-0 位(掩码 0x007fffff 选定的位)表示浮点数的有效位数(有时也称为尾数)。这很好,不过有一点,它的最高位是符号位,正数0,负数1。这样就有点问题了。
那么我们怎么解决这个问题呢?如果这个float是正数,那么把它看成int也是正数,而且根据前面的说明,指数在前,所以顺序也是保持好的。如果它是个负数,把它看出int也是负数,但是顺序就反了,举个例子 <4,-0.2> <3, -0.5>,如果不看符号,显然是前者大,但是加上符号,那么正好反过来。也就是说,负数的顺序需要反过来,怎么反过来呢? 就是符号位不变,其它位0变成1,1变成0?具体怎么实现呢?还记得异或吗?1 ^ 0 = 1; 1 ^ 1 = 0,注意左边那个加粗的1,然后看第二个操作数,也就是想把一个位取反,那么与1异或运算就行了。类似的,如果想保持某一位不变,那么就让它与0异或。
因此我们可以发现NumericUtils有这样一个方法,就是上面说的实现。
/**
* Converts a <code>float</code> value to a sortable signed <code>int</code>.
* The value is converted by getting their IEEE 754 floating-point "float format"
* bit layout and then some bits are swapped, to be able to compare the result as int.
* By this the precision is not reduced, but the value can easily used as an int.
* @see #sortableIntToFloat
*/
public static int floatToSortableInt(float val) {
int f = Float.floatToRawIntBits(val);
if (f<0) f ^= 0x7fffffff;
return f;
}
3.2 一个int可以转换成一个字符串,并且保持顺序
我们这里考虑的是java的int,也就是有符号的32位正数,补码表示。如果只考虑正数,从0x0-0x7fffffff,那么它的二进制位是升序的(也就是把它看成无符号整数的时候);如果只考虑负数,从0x10000000-0xffffffff,那么它的二进制位也是升序的。唯一美中不足的就是负数排在正数后面。
因此如果我们把正数的最高符号位变成1,把负数的最高符号位变成0,那么就可以把一个int变成有序的二进制位。
我们可以在intToPrefixCoded看到这样的代码:int sortableBits = val ^ 0x80000000;
因为lucene只能索引字符串,那么现在剩下的问题就是怎么把一个4个byte变成字符串了。Java在内存使用Unicode字符集,并且一个Java的char占用两个字节(16位),我们可能很自然的想到把4个byte变成两个char。但是Lucene保存Unicode时使用的是UTF-8编码,这种编码的特点是,0-127使用一个字节编码,大于127的字符一般两个字节,汉字则需要3个字节。这样4个byte最多需要6个字节。其实我们可以把32位的int看出5个7位的整数,这样的utf8编码就只有5个字节了。这段代码就是上面算法的实现:
int sortableBits = val ^ 0x80000000;
sortableBits >>>= shift;
while (nChars>=1) {
// Store 7 bits per character for good efficiency when UTF-8 encoding.
// The whole number is right-justified so that lucene can prefix-encode
// the terms more efficiently.
buffer[nChars--] = (char)(sortableBits & 0x7f);
sortableBits >>>= 7;
}
首先把val用前面说的方法变成有序的二进制位。然后把一个32位二进制数变成5个7位的正数(0-127)。
总结一下,我们可以通过上面的方法把Java里常见的数值类型(int,float,long,double)转成字符串,并且保持顺序。【大家可以思考一下其它的类型比如short】。这样很好的解决了用原来的方法需要给整数补0的问题。
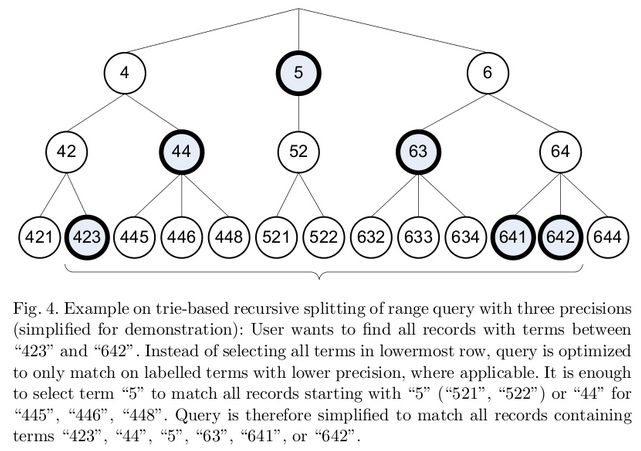
现在我们来看看第二个问题:范围查询时需要展开的term太多的问题。参考下图:
引自Schindler, U, Diepenbroek, M, 2008. Generic XML-based Framework for Metadata Portals. Computers & Geosciences 34 (12)
我们可以建立trie结构的索引。比如我们需要查找423--642直接的文档。我们只需要构建一个boolean or query,包含6个term(423,44,5,63,641,642)就行了。而不用构建一个包含11个term的query。当然要做到这点,那么需要在建索引的时候把445和446以及448的docId都合并到44。怎么做到这一点呢?我们可以简单的构建一个分词器。比如423我们同时把它分成3个词,4,42和423。当然这是把数字直接转成字符串,我们可以用上面的方法把一个整数变成一个UTF8的字符串。但现在的问题是怎么索引它的前缀。比如在上图中,我们把423“分词”成423,42,4;类似的,我们可以把一个二进制位也进行“前缀”分词,比如6的二进制位表示是110,那么我们可以同时索引它的前缀11和1。当然对于上图,对于423,我们可以只分词成423和4,也就是只索引百位,这样trie索引本身要小一些,对某些query,比如搜索300-500,和原来一样,只需要搜索term “4”,但是某些query,比如搜索420-450,那么需要搜索更多的term。
因此NumericRangeQuery有一个precisionStep,默认是4,也就是隔4位索引一个前缀,比如0100,0011,0001,1010会被分成下列的二进制位“0100,0011,0001,1010“,”0100,0011,0001“,”0100,0011“,”0100“。这个值越大,那么索引就越小,那么范围查询的性能(尤其是细粒度的范围查询)也越差;这个值越小,索引就越大,那么性能越差。这个值的最优选择和数据分布有关,最优值的选择只能通过实验来选择。
另外还有一个问题,比如423会被分词成423,42和4,那么4也会被分词成4,那么4表示哪个呢?
所以intToPrefixCoded方法会额外用一个char来保存shift:buffer[0] = (char)(SHIFT_START_INT + shift);
比如423分词的4的shift是2(这里是10进制的例子,二进制也是同样的),423分成423的shift是0,4的shift是0,因此前缀肯定比后缀大。
注意: 这里概念上是一棵trie树, 实际存储的方式不像一般的树结构, 一般的树结构, 是一个节点会有指向孩子节点的指针, 同时会有指向父节点的指针. Lucene由于是按照索引方式存储的, 只是通过计算可以知道一个term对应的父节点(前缀term). shift=0的前缀, 可以逻辑上看做是trie树的叶节点, shift=1的前缀, 是上一层的父节点, 依次类推. 之所以说是逻辑上, 是由于这些shift=0, shift=1之类的前缀, 在lucene里都是对应一个分词, 至于两个分词之间的关系, 是通过计算确定的.
上面说了怎么索引,那么Query呢?比如我给你一个Range Query从423-642,怎么找到那6个term呢?
我们首先可以用shift==0找到范围的起点后终点(有可能没有相等的,比如搜索422,也会找到423)。然后一直往上找,直到找到一个共同的祖先(肯定能找到,因为树根是所有叶子节点的祖先),对应起点,每次往上走的时候, 左边范围节点都要把它右边的兄弟节点都加进去, 右边范围节点都要把它左边的兄弟节点加进去, 若已经到达顶点, 则是将左边范围节点和右边范围节点之间的节点加进行去.
查找423到642之间的具体的区间:
423-429,640-642
43-49,60-63
5-5
最后,看看实际的代码:
(1). 创建索引时的代码, 数字的分词实现, NumericTokenStream类:
@Override
public boolean incrementToken() {
if (valSize == 0)
throw new IllegalStateException("call set???Value() before usage");
if (shift >= valSize)
return false;
clearAttributes();
final char[] buffer;
switch (valSize) {
case 64:
buffer = termAtt.resizeTermBuffer(NumericUtils.BUF_SIZE_LONG);
termAtt.setTermLength(NumericUtils.longToPrefixCoded(value, shift, buffer));
break;
case 32:
buffer = termAtt.resizeTermBuffer(NumericUtils.BUF_SIZE_INT);
termAtt.setTermLength(NumericUtils.intToPrefixCoded((int) value, shift, buffer));
break;
default:
// should not happen
throw new IllegalArgumentException("valSize must be 32 or 64");
}
typeAtt.setType((shift == 0) ? TOKEN_TYPE_FULL_PREC : TOKEN_TYPE_LOWER_PREC);
posIncrAtt.setPositionIncrement((shift == 0) ? 1 : 0);
shift += precisionStep;
return true;
}
(2) 范围搜索时的处理代码:
/** This helper does the splitting for both 32 and 64 bit. */
private static void splitRange(
final Object builder, final int valSize,
final int precisionStep, long minBound, long maxBound
) {
if (precisionStep < 1)
throw new IllegalArgumentException("precisionStep must be >=1");
if (minBound > maxBound) return;
for (int shift=0; ; shift += precisionStep) {
// calculate new bounds for inner precision
// 本次处理的范围值
final long diff = 1L << (shift+precisionStep),
// mask, 只取本次精度的范围值
mask = ((1L<<precisionStep) - 1L) << shift;
System.out.println("diff=" + diff);
System.out.println("mask=" + Integer.toBinaryString((int) mask));
final boolean
// 当最小界限不是范围的最小值时,则本层次最小界限有值,否则已经是本层级的最小值了,那么可以直接移到上一层,因为上一层包含本层的所有值
hasLower = (minBound & mask) != 0L,
// 当最大界限不是范围的最大值时,则本层次最大界限有值,否则已经是本层级的最大值了,那么可以直接移到上一层,因为上一层包含本层的所有值
hasUpper = (maxBound & mask) != mask;
final long
// 移到上一层
nextMinBound = (hasLower ? (minBound + diff) : minBound) & ~mask,
nextMaxBound = (hasUpper ? (maxBound - diff) : maxBound) & ~mask;
final boolean
lowerWrapped = nextMinBound < minBound,
upperWrapped = nextMaxBound > maxBound;
if (shift+precisionStep>=valSize || nextMinBound>nextMaxBound || lowerWrapped || upperWrapped) {
// We are in the lowest precision or the next precision is not available.
addRange(builder, valSize, minBound, maxBound, shift);
// exit the split recursion loop
break;
}
if (hasLower)
// min->minMax
addRange(builder, valSize, minBound, minBound | mask, shift);
if (hasUpper)
// maxMin->max
addRange(builder, valSize, maxBound & ~mask, maxBound, shift);
// recurse to next precision
minBound = nextMinBound;
maxBound = nextMaxBound;
}
}
本文主要内容参考博客:http://blog.csdn.net/fancyerii/article/details/7256379,主要是看到此文已经讲得比较明白了,具体也可参考NumericField的类的文档说明。