Huffman codes

简介

    在很早以前的时候有学习过huffman编码，凭借当年的一点学习的印象只是知道它是一种有效的存储和压缩数据的方式。至于这种编码背后的思路是什么，它为什么能带来有效的编码压缩效果都没有深究。这里结合最近学习的一点感悟做一步的讨论。

 

Huffman编码的引入

    在详细介绍huffman编码之前，我们可以先考虑一个典型的字符编码和存储的场景。假定有一个含有100000个字符的文件，它里有很多个字符。我们经过统计之后发现出现的字符主要有6个，分别为a, b, c, d, e, f。他们出现的频率如下表所示：

	a	b	c	d	e	f
出现频率	45000	13000	12000	16000	9000	5000
编码	000	001	010	011	100	101

    因为我们知道一个字符存储需要两个字节，而我们这里需要对字符进行压缩，所以希望能用尽可能少的字节来表示他们。而为了尽可能简洁的来表达这些字符，对于这6个元素来说，我们可以采用3个位来表示他们。所以这里a到f分别用000到101表示。如前面表所示。按照这种做法，我们发现这种编码方式生成的文件占用空间大小为100000 * 3 bit = 300000bit。和前面100000 * 2byte = 200000 byte比起来，确实有比较大的压缩效果改进。

改进

    前面的编码方式看起来已经有了不小的进步。我们还有没有改进的空间呢？我们来看前面选择编码的思路。因为我们总共有6个字符，如果用2进制来表示的话，至少要3个位，所以就采用了3个。这里考虑仅仅是有多少个字符要表示。这是一个方面。可是，我们忽略了另外一个方面。在文件里，每个字符有它出现的频率，比如a出现的频率最高，f出现的频率最低。有没有可能我们让出现频率越高的字符尽量短，而出现频率低的字符可以稍微长一点呢？比如前面的示例中，我们是所有字符的长度都是平均的3位，如果我们对于频率最高的那个字符直接用一个位来描述，这样岂不是更省空间？比如前面字符a出现了45000次，如果我们只是用一个位来表示它的话，则省下了90000个位。当然，对于这一步来说它确实是省到了。如果按照这个思路来，我们后续的字符该怎么编码呢？我们需要用没有歧义的编码来表示这些字符。而前面第一种方法所能表示的极限就是3个位。如果这里我们直接就用去了一个位，要表示后面5个元素，会不会导致某些元素要使用更多的位呢？

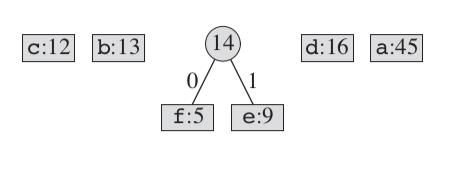
    其实，这就是huffman里面采取的一个策略。我们充分利用统计的结果，将频率高的字符编码尽可能设的短，而频率低的设的稍微长一些。因为频率高的带来的空间节约比频率低带来的空间消耗要多，所以能够实现更进一步的空间压缩。比如说，我们在前面的问题里，假定有3个字符要编码。按照我们刚才的情况，a已经占用了字符0,而另外两个字符只能是10, 11了。他们的编码情况如下图：

    这里，a的编码是0, b的编码是10，c的编码是11。和前面那种按字符编码的方式来说，这种方式确实做到了某些字符很短，带来的代价是某些字符的编码会变得长一些。这里，我们难免会有另外一个问题。为什么我们要这样来编码，不能把b编码成00, c编码成01吗？

    在这里，如果按照这种方式编码的话是不合理的。因为我们要考虑到编码以后要解码时的问题。如果a编码成0，b编码成00，c编码成01了。我们碰到一组01串如001010时，这会儿编码就会产生歧义，我们是应该将第一个0解析成a呢还是将前面两个0解析成b呢？所以，为了更加高效率的解析这些字符，我们必须保证一个字符的编码不是另外一个字符编码的前缀。

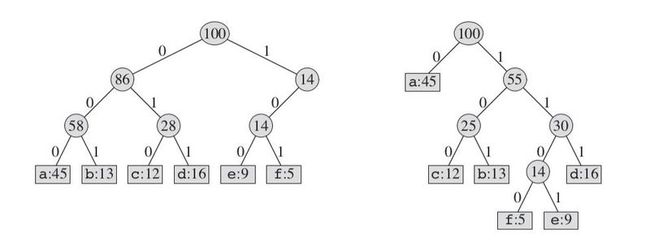
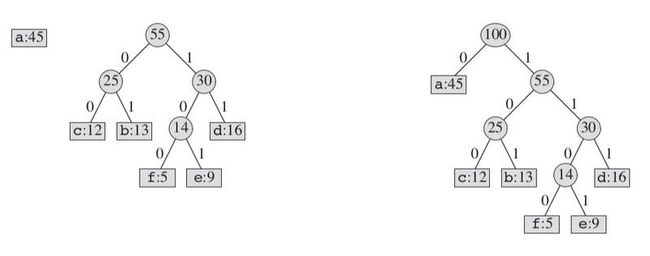
    以我们前面讨论的示例为基础，基于字符数量和字符频率编码的这两种思路，产生的编码结果比较如下图：

    如果我们详细计算按照后面这种编码方式占用的空间的话，后面这种的位数为: 224000。

 

Huffman树的构造

    前面示例中只是展示了一个huffman编码的结果，具体的huffman树该如何构造呢？按照我们前面讨论的思路，越频繁的字符编码越短。反过来说，出现次数越少的字符编码越长。我们可以倒过来，从叶节点来构造整棵树。

    我们首先选择频率最低的两个节点，然后将他们归并到一个节点下。这个新构造的节点的频率为两个子节点的频率之和。然后将这个新生成加入到取出了两个子节点的集合中，再重复原来的过程。这样我们就得到最终的huffman树。以前面的示例来考虑，我们这6个节点中，频率最低的是e和f。我们第一步则构造一个合并它们两个的节点，如下图：

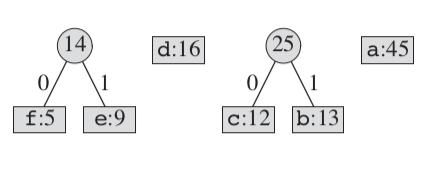
    这里的一个要点是我们新构造的这个节点，它的频率为e和f频率的和。我们将这个节点当作一个字符加入到原来的集合里，然后再按照前面的过程来选取频率最低的两个：

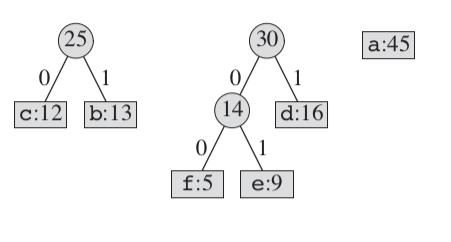
    按照这个过程，后面的流程如下：

 

    现在，我们已经知道怎么来构造huffman树了。我们从具体实现的角度来看看。

    我们这里的要点是每次选择最小的两个元素，然后将他们归并到一个新节点下。而新节点的频率值为两个节点的和。那么，我们是不是需要将这些元素都排序呢？如果我们排序的话，可能需要O(nlgn)的时间。但是我们每次移除了两个最小元素之后又要将他们的和加入到集合中来，这样就破坏了原来的顺序性。看来直接排序然后拿过来用的效果并不理想。这个时候，如果我们回想起以前用的数据结构堆来，会发现它是解决这个问题的一个理想选择。

实现讨论

    我们建一个堆花费的时间为O(n)，比排序要好一些。另外，每次取两个最小的元素，所以应该是一个最小堆。将新构造的元素加入到堆中，之需要堆做一个调整，时间复杂度为O(lgn)。看来整体情况确实很理想。关于堆和最小堆的分析，可以参考我前面的堆排序这篇文章和priority queue这篇文章。

    我们这里既然是用的最小堆，那完全可以直接使用最小堆来保存所有这些元素。另外，这些元素要构成一个huffman树，我们需要定义每个元素成一个树节点的样式。感觉这里是最小堆和二叉树的结合。

    根据这里的讨论，下面是一个参考实现：

import java.util.PriorityQueue;
import java.util.List;
import java.util.ArrayList;

public class Huffman {

    public static class Node implements Comparable<Node> {
        private int freq;
        private char c;
        private Node left;
        private Node right;

        public Node(int freq, char c) {
            this.freq = freq;
            this.c = c;
        }

        public Node(int freq) {
            this.freq = freq;
        }

        public Node getLeft() {
            return left;
        }

        public Node getRight() {
            return right;
        }

        public void setLeft(Node left) {
            this.left = left;
        }

        public void setRight(Node right) {
            this.right = right;
        }

        public int getFreq() {
            return freq;
        }

        @Override
        public int compareTo(Node node) {
            return this.freq - node.getFreq();
        }
    }

    public Node encode(List<Node> list) {
        PriorityQueue<Node> queue = new PriorityQueue<Node>(list);
        for(int i = 0; i < list.size() - 1; i++) {
            Node x = queue.poll();
            Node y = queue.poll();
            Node z = new Node(x.getFreq() + y.getFreq());
            z.setLeft(x);
            z.setRight(y);
            queue.add(z);
        }
        return queue.poll();
    }

    public void printEncodedTree(Node node) {
        if(node != null) {
            System.out.println(node.getFreq() + " ");
            printEncodedTree(node.getLeft());
            printEncodedTree(node.getRight());
        }
    }

    public static void main(String[] args) {
        Huffman huffman = new Huffman();
        List<Node> list = new ArrayList<Node>();
        list.add(new Node(45, 'a'));
        list.add(new Node(13, 'b'));
        list.add(new Node(12, 'c'));
        list.add(new Node(16, 'd'));
        list.add(new Node(9, 'e'));
        list.add(new Node(5, 'f'));
        Node node = huffman.encode(list);
        System.out.println(node.getFreq());
        huffman.printEncodedTree(node);
    }
}

    这部分代码看起来比较长，主要是充分利用了jdk类库里现有的PriorityQueue。当然，如果我们有兴趣也可以参考我前面关于堆的文章自己来实现一个。另外，这部分代码里一个比较有意思的地方就是我们定义的节点Node必须是可以比较的。因为我们从前面的讨论里也看到，我们每次要挑选最小的元素出来，怎么挑呢？肯定需要比较。所以这里采用一种实现Comparable接口的方法。当然，关于怎么使用PriorityQueue，可以参考后续的文档。代码中还有一个有意思的地方就是在encode方法里，我们是循环遍历n-1次，这样最后PriorityQueue里剩下一个元素，这个元素就是我们要构造出来的树的根节点。

    为了能够看到整个树的结果，这里用一个简单的前序遍历方法打印出来了每个节点的频率值。

前面程序运行的结果如下：

100
100 
45 
55 
25 
12 
13 
30 
14 
5 
9 
16 

    前面程序实现的是huffman编码。如果我们还需要解码，该怎么来做呢？这里我们也做一个简单的概括，代码再后续补上。因为这里编码的每个字符都是唯一的。我们可以每次读进一个数字的时候就对应在树里遍历一步。比如说当前读到的是0,则转向左子节点，否则到右子节点。如果这个时候发现已经到叶节点了，这个时候可以将这几个数字编码对应的字符输出。我们可以用一个HashMap来事先保存好他们之间的映射关系。这样每次遍历到一个叶节点构成一个数字序列时我们可以直接取出对应的字符来。

 

总结

    Huffman编码其实本质上并不复杂。它的背后也有一种贪心算法的思路。我们在确定一个频率越高编码越短的前提之后，每次尽量将频率低的放到长一点的叶节点上。具体关于它们为什么是最优的，我们可以参考书上面的证明，这里就不再赘述了。

 

参考材料

Introduction to algorithms

http://stackoverflow.com/questions/683041/java-how-do-i-use-a-priorityqueue