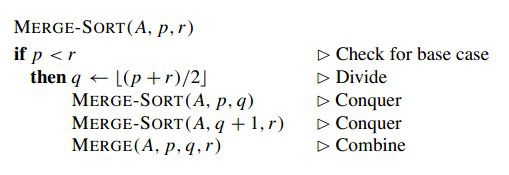【算法导论】排序(一)
虽然久闻大名,但第一次接触算法导论,是看了网易公开课MIT的《算法导论》课,记得 第一集就讲到了插入排序和归并排序。
几个星期前也买了算法导论这本书,准备慢慢啃~
这星期主要在看前两部分,除了对于讲渐进时间、递归式分析这些东西感到云里雾里的,其它的都就
感觉越看越有觉得入迷,果然不愧是一本经典之作![]()
好吧,开始。本文主要是用C++把书中的算法实现,以及一些笔记。
一、插入排序。
插入算法的设计使用的是增量(incremental)方法:在排好子数组A[1..j-1]后,将
元素A[ j]查入,形成排好序的子数组A[1..j]
插入排序的效率为O(n^2),在数据规模较小的时候效率较高。
最佳的情况是一个数组已经是排好序的,只需O(n)。最坏情况是输入数据是逆序的, O(n^2)。 对于一个算法,一般是考察它的最坏情况运行时间
.
伪代码:这里需要注意的是由于大部分编程语言的数组都是从0开始算起,而伪代码是从1开始的

C++实现:
template <typename T>
void insert_sort(T *begin, T *end){ // 采用了更接近C++ STL sort的调用方式
T *p,*t,key;
for(p=begin+1; p!=end; ++p){
// 把A[j]插入排好序的A[1...j-1]中
key = *p;
t=p-1;
while(t>=begin && *t>key){
*(t+1) = *t;
--t;
}
*(t+1) = key;
}
}
记得曾在刘汝佳的《算法竞赛入门经典》中看到一段代码,书上说是冒泡排序,但是却和冒泡排序的过程有点不一样。一直到最近才知道,
原来那个应该算作是交换排序。
选择排序伪代码:
冒泡排序伪代码:
// 选择排序
void select_sort(int *start,int *end){
int *p,*q,*min;
for(p=start; p<end; ++p){
min=p;
for(q=start+1; q<end; ++q){
if(*q<*min)
min=q;
}
Swap(min,p);
}
}
// 冒泡排序
void bubble_sort(int *start,int *end){
int *p,*q;
for(p=start; p<end; ++p){
for(q=end-1; q>start; --q){
if(*q<*(q-1))
Swap(q,q-1);
}
}
}
这三个排序的效率都为O(n^2)
从中可以看出,选择排序和冒泡排序都是从当前位置i的后面所有数中最小的一个数,交换到i位置中,但是选择排序只需要交换一次,冒泡排序可能会交换多次,速度应该是选择排序更快。。
除了选择排序和冒泡排序,还有一个叫”交换排序“的,思想也几乎一样,它是分别将第 i 个数 和后面的数一一比较,一旦后面的一个数比它小,就交换。
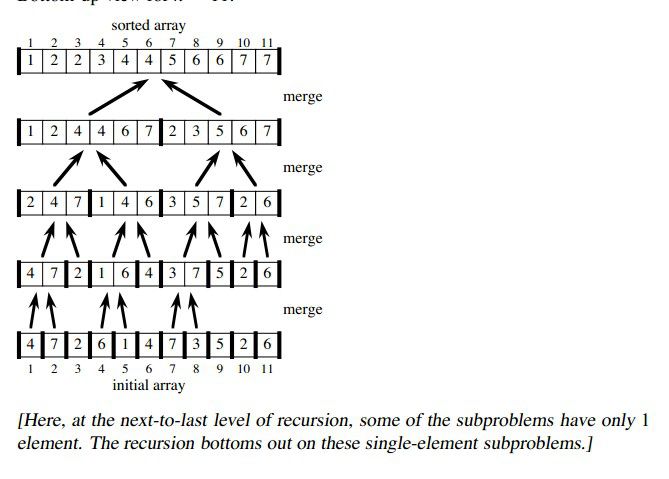
三、归并排序(合并排序)
归并排序是一种高效的排序算法,按照分治三步法:
划分问题:把序列分成元素个数尽量相等的两半
递归求解:把两半元素分别排序
合并问题:把两个有序表合并成一个
MERGE-SORT伪代码:
MERGE是关键:
这里给的代码实现是在每一堆的底部放一张“哨兵卡”,可以用于简化代码。
但是我用C++实现的方式采用另外一种形式,放“哨兵卡”虽然可以简化代码,但是这个“哨兵值”却有点局限性,在不同平台和机器下可能会不同。
// 算法导论实现版本
template<typename T>
void merge(T array[],int p,int q,int r){
int n1,n2,i,j,k;
n1=q-p+1;
n2=r-q;
T *left=new T[n1], *right=new T[n2];
for(i=0; i<n1; ++i) // 对左数组赋值
left[i] = array[p+i];
for(i=0; i<n2; ++i) // 对又数组赋值
right[i] = array[q+i+1];
i=j=0;
k=p;
while(i<n1 && j<n2){
if(left[i] <= right[j])
array[k++] = left[i++];
else
array[k++] = right[j++];
}
for( ; i<n1; ++i) //如果左数组有元素剩余,则将剩余元素合并到array数组
array[k++] = left[i];
for( ; j<n2; ++j) //如果右数组有元素剩余,则将剩余元素合并到array数组
array[k++] = right[j];
delete [] left; // 记住要释放空间
delete [] right;
}
template<typename T>
void merge_sort(T array[],int p,int r){
if(p<r){
int q = (p+r)/2;
merge_sort(array,p,q);
merge_sort(array,q+1,r);
merge(array,p,q,r);
}
}
并归排序在ACM中有个用处,可以用来求逆序数对(《算法竞赛入门经典》P144),因为如果直接枚举的效率为O(n^2)会超时。
受并归排序启发,由于合并操作是从小到大进行的,当右边的A【j】复制到T中时(这里的T是刘汝佳版的并归排序实现,后面给出),左边还没来得及复制到T得那些数就是左边所有比A【j】大的数,即A【j】的逆序数
刘汝佳神牛的并归排序+顺便求出逆序数
void merge_sort(int *A,int x,int y,int *T){ // T是专门开得一个临时数组。 这样可以大大节约了很多时间(上面的方式要多次开辟数组空间)
if(y-x > 1){
int m=x+(y-x)/2; // 划分
int p=x, q=m, i=x;
merge_sort(A,x,m,T);
merge_sort(A,m,y,T);
while(p<m || q<y){ // 非递归调用的方式还可以节省栈调用时间
if(q>=y || (p<m && A[p] <= A[q])) T[i++] = A[p++];
else { T[i++] = A[q++]; cnt += m-p; } // cnt用来计算逆序数对,用全局变量,调用前清零
}
for(i=x; i<y; ++i) A[i]=T[i];
}
}
—— 生命的意义,在于赋予它意义。