mahout源码canopy算法分析之三CanopyReducer

经过了前面两篇文章的分析，相信大家对CanopyReducer的分析就不会碰到太大的疑问，因为CanopyReducer的操作简直就和CanopyMapper的操作一模一样，也是把所有的样本数据分为若干组，即又按照map的操作执行了一次，那么就会有同学问了？那不是都不需要用reduce么？大家这里想一下，map的输出和输入有什么区别。假如map的输入有100个样本被分为了5组，并且clusterFilter设置为15那么，map输出5个样本，reduce针对这5组也输出5个canopy，但是还要加一个步骤，过滤。总共才5组，用clusterFilter=15去过滤，就算这5个样本都被分为了一个组，那也要被过滤掉了，所以reduce没有输出？首先要说明的是，reduce必须要，下面详细分析。

首先画个图来解释，mapreduce过程：

map 输入数据为样本点，在map过程之前被分为了两个map，每个map含有一部分的数据。比如map1的数据，针对每个样本点遍历所有的canopy，若该样本和canopy的距离满足<t1且>t2或者>t1，则把该样本作为一个新的canopy加入canopy集中，map1的输出。整合所有map的输出（相同的key，这里的key可以看到都是设置为一样的），作为reduce的输入，然后reduce重复map过程即可得到reduce的输出，这个要如何验证呢？

下面用程序验证，可以下载MahoutCanopy.jar包，以便直接运行或者下载源码进行分析；

准备工作：

1.数据：1.txt

8,8
7,7
6.1,6.1
9,9
2,2
1,1
0,0
2.9,2.9

2.txt:

8.1,8.1
7.1,7.1
6.2,6.2
7.1,7.1
2.1,2.1
1.1,1.1
0.1,0.1
3.0,3.0

然后把上面的代码上传到hdfs文件系统上面的input/test_canopy上面；

2. 把下载的MahoutCanopy.jar包放入到hadoop的lib下面，且放入java工程的lib路径下，运行下面的程序：

package mahout.test.canopy.fansy;
import mahout.fansy.canopy.CanopyDriver;
public class CanopyTest {

	public static void main(String[] args) throws Exception {
		String[] arg={"-fs","hadoop:9000","-jt","hadoop:9001",
				"--input","hdfs://hadoop:9000/user/hadoop/input/test_canopy",
				"--output","hdfs://hadoop:9000/user/hadoop/output/test_canopy",
				"--distanceMeasure","org.apache.mahout.common.distance.ManhattanDistanceMeasure",
				"--t1","8","--t2","4",
				"--clusterFilter","1","--method","mapreduce"};
		CanopyDriver.main(arg);
	}
}

下面结合log信息来说明概算法的数据流逻辑：

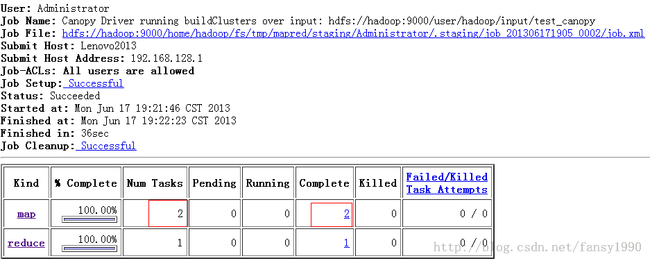
由上面的图可以看到，有两个map，其实如果按照真实的环境来说的话应该是当数据超过64M的时候才会有多个map，我这里把数据认为的分为了两个文件，等于就是同样的操作了，为的就是产生两个map。产生两个map就可以看到后面在reduce的数据的合并。

先说map1：

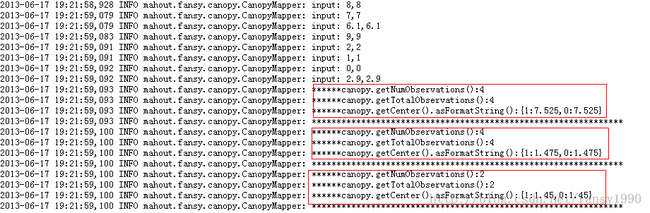
可以看到这个输入是2.txt文件，这里的t1=8，t2=4，下面解释第二个红色框

首先针对第一个样本[8.1,8.1]，因为之前没有canopy，所以[8.1,8.1]被设置为第一个canopy，这时canopies={[8.1,8.1]}；第二个样本[7.1,7.1]由于它到[8.1,8.1]的曼哈顿距离为2<t2=4，所以这时canopies(1)的个数变为2，且canopies中canopy的个数没有变；第三个样本[6.2,6.2]它和canopies(1)=[8.1,8.1]的距离是3.8<t2=4，所以canopies(1)的个数变为3（即这时在[8.1,8.1]这个canopy内的样本数是3个）；第四个样本[7.1,7.1],所以canopies(1)的个数变为4个，其他不变；第五个样本[2.1,2.1]它到canopies(1)的曼哈顿距离=8>=t1=8,flag=false;所以要新建一个canopy，所以这时canopies(1)=[8.1,8.1] 其样本数是4个,canopies(2)=[2.1,2.1]其样本数是1个；第六个样本[1.1,1.1]其到canopies(1)的距离>t1=8,flag=false，所以canopies(1)的样本数不增加；然后样本到canopies(2)的距离为2<t1=8,但是2<2=4，所以flag=true，所以[1.1,1.1]不加入到canopies中，这时canopies={[8.1,8.1]：4,[2.1,2.1]：2}；第七个样本[0.1,0.1]到canopies(1)的距离>t1=8，flag=false，到canopies(2)的距离4<t1=8 但是>=t2=4,flag=false所以[0.1,0.1]要加入canopies中，且canopies(2)的样本数加1，这时canopies={[8.1,8.1]：4,[2.1,2.1]：3,[0.1,0.1]：1}；最后一个样本后，canopies={8.1,8.1]：4,[2.1,2.1]：4,[0.1,0.1]：2}。这个数据对应上面的后面三个红色方框，其中的center对应于什么呢？对应于每组中的平均值：分组如下：第一组：{样本1，样本2，样本3，样本4}，第二组：{样本5，样本6，样本7，样本8}，第三组：{样本7，样本8}。（上面的分析过程对应于CanopyCluster的addPointToCanopies方法，其中flag为false时才能添加一个canopy到canopies中）；

这样等于map1输出如下：

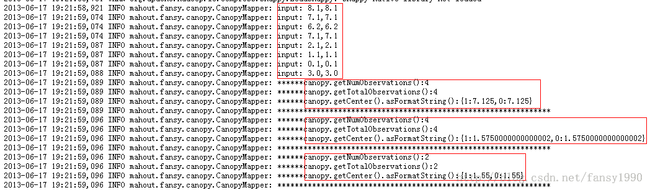
7.125,7.125
1.575,1.575
1.55,1.55

map2如下图：

查看reduce的输入：

这个数据和前面的map的数据刚好对应上了，说明前面的假设成功，即canopy的mapreduce数据流就是按照上面的来走的。

分享，快乐，成长

转载请注明出处：http://blog.csdn.net/fansy1990