FP-growth Algorithm 笔记

FP-growth Algorithm (Frequent Pattern Algorithm, 频繁模式算法), 只需要对数据库进行两次扫描, 即可发现频繁项集, 它比 Apriori 算法更高效, 但 FP-growth 算法不能用于发现关联规则.

优点	一般要快于 Apriori
缺点	实现比较困难, 在某些数据集上性能会下降
适用数据类型	标称型

基础概念
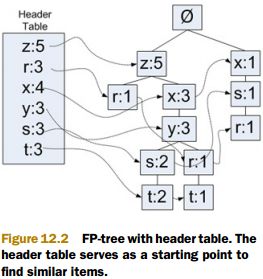
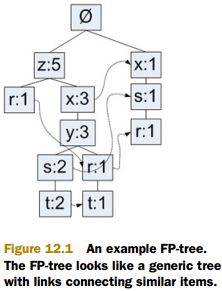
1. FP 树

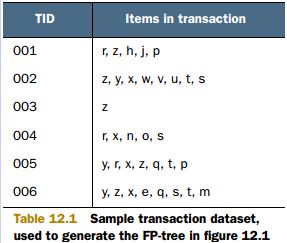
FP 树将每个集合以路径的方式存储在树中, 从根节点开始, 每个条路径上的节点按其出现频数递减. 存在相似元素的集合会共享树的一部分, 只有当集合之间出现不同时, 树才会分叉. 图示如下(左图是数据, 右图是最小支持度为 3 的 FP树):
                   

2. 头指针表
链表, 每个节点存放的是某一元素项, 及其在所有集合中出现的总次数, 及指向FP树各个分支上同样元素的指针. 从头指针表, 可以快速定位到各个分枝上的元素. 头指针表图示如下:

3. 条件模式基(conditional pattern base)
从头指针表中的单个频繁元素开始, 对每个路径中的此元素, 向根节点回溯, 每一条回溯路径上的节点都组成一个集合. 即前缀路径. 

4. 条件 FP 树
使用 3 中的得到的各个前缀路径, 作为新的数据集合, 并按 1 中的方法构造出来的 FP 树, 即为 条件FP树.在构造条件 FP 树时, 同样要通过最小支持度来淘汰非频繁项.

算法描述
1. 构造 FP 树
(1). 遍历每个集合, 对此集合中的元素, 按其在总数据集中出现的次数排序, 并去除掉未达到最小支持度的元素.
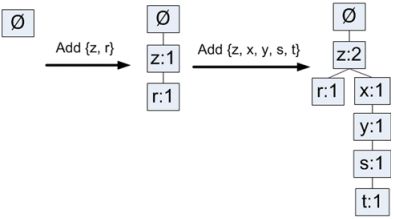
(2). 对每个集合, 从树的根节点依次往下插入, 如果节点已存在, 则递增节点的计数值, 否则创建一个分支.如下图:

(3). 对树中每一个新加入的节点, 都要在头指针表中查找, 如果头指针表中没有此元素, 就在头指针表中创建一个此元素节点节点; 把新加入元素接入到头指针表中此元素所对应链表的最后, 并把头指针表中此元素的计算递增.
(4). 循环 (2) -> (3), 直至所有集合操作完毕.

2. 从 FP 树挖掘频繁项集
(1). 取头指针表的第一个频繁元素, 遍历其所在的各条树路径
(2). 在每个树路径中, 都向根节点回溯, 得到条件模式基
(3). 以 (2) 中得到的条件模式基创建新的 FP 树
(4). 对 FP 树按 (1) ->(3) 递归挖掘
(5). 每次循环时, (1) 中所取的频繁项元素, 与递归传进来的前缀合成频繁项集. (代码 118, 119 行) 即每层递归的每个头指针列表中的每个频繁元素都会生成一个频繁项集.

算法流程图
1. 构造 FP 树

2. 从 FP 树挖掘频繁项集

代码

# -*- coding: utf-8 -* 
# 树节点
class treeNode:
    def __init__(self, nameValue, numOccur, parentNode):
        self.name = nameValue
        self.count = numOccur         # 计数值
        self.nodeLink = None          # 连接相似变量
        self.parent = parentNode      #needs to be updated
        self.children = {} 
    
    def inc(self, numOccur):
        self.count += numOccur
    
    # 递归输出树节点
    def disp(self, ind=1):
        print '  '*ind, self.name, ' ', self.count
        for child in self.children.values():
            child.disp(ind+1)


# 根据 dataSet 创建 FP-growth 树
# 参数 minSup 指的是最小支持度
def createTree(dataSet, minSup=1): 
    headerTable = {}
    
    # 遍历所有元素项, 记录其出现次数
    # 内容类似为 {'t': 3, 'w': 1, 'v': 1, 'y': 3, 'x': 4, 'z': 5}
    for trans in dataSet:
        for item in trans:
            headerTable[item] = headerTable.get(item, 0) + dataSet[trans]

    # 移除未达到最小支持度的元素项
    for k in headerTable.keys():  
        if headerTable[k] < minSup: 
            del(headerTable[k])

    freqItemSet = set(headerTable.keys())
    if len(freqItemSet) == 0: return None, None  # 没有达到最小支持度的元素项, 返回

    # 格式化后格式为: 
    # {'t': [3, None], 'y': [3, None], 'x': [4, None], 'z': [5, None]}
    for k in headerTable:
        headerTable[k] = [headerTable[k], None] 

    retTree = treeNode('Null Set', 1, None)     # 只包含空值的根节点
    
    for tranSet, count in dataSet.items():      # count 都初始化为 1
        localD = {}
        for item in tranSet:                    # 取满足最小支持度的元素项
            if item in freqItemSet:
                localD[item] = headerTable[item][0]

        # 对每个项集中的元素项, 按支持度从大到小排序
        if len(localD) > 0:
            orderedItems = [v[0] for v in sorted(localD.items(), 
                            key=lambda p: p[1], reverse=True)]
            updateTree(orderedItems, retTree, headerTable, count)   # 填充树
    return retTree, headerTable                 # 返回树与各个元素的头指针


# 使用 items 使树生长, FP-growth 的来历
# inTree 为树的根节点
def updateTree(items, inTree, headerTable, count):
    # 如果 items 的第一个元素是 树的第一层子节点, 则将此子节点对应的计算 加1
    if items[0] in inTree.children:
        inTree.children[items[0]].inc(count) 
    else:   # 如果此节点不存在, 则给树添加新子节点
        inTree.children[items[0]] = treeNode(items[0], count, inTree)
        # 更新头指针表
        if headerTable[items[0]][1] == None: 
            headerTable[items[0]][1] = inTree.children[items[0]]
        else:
            updateHeader(headerTable[items[0]][1], inTree.children[items[0]])

    # 对除去第一个元素之外的 items 递归建树
    if len(items) > 1:
        updateTree(items[1::], inTree.children[items[0]], headerTable, count)
        

# 更新头指针链表, targetNode 接到 nodeToTest 所指链表的最后
# 这里不用递归, 因为递归在链表长度过长时, 可能会栈溢出
def updateHeader(nodeToTest, targetNode):   
    while (nodeToTest.nodeLink != None):    
        nodeToTest = nodeToTest.nodeLink
    nodeToTest.nodeLink = targetNode
        

# 迭代上溯整棵树
# 即将叶节点到根节点的所有元素都存到 prefixPath 中
def ascendTree(leafNode, prefixPath): 
    if leafNode.parent != None:
        prefixPath.append(leafNode.name)
        ascendTree(leafNode.parent, prefixPath)


# 按给定元素项生成一个条件模式基
# 遍历头指针链表, 对每一个元素都向根节点上溯, 记录找到的前缀式及元素出现次数
def findPrefixPath(basePat, treeNode): #treeNode comes from header table
    condPats = {}
    # 遍历以 treeNode 为头节点的头指针链表
    while treeNode != None:
        prefixPath = []
        ascendTree(treeNode, prefixPath)
        # 保存前缀及其次数
        if len(prefixPath) > 1: 
            condPats[frozenset(prefixPath[1:])] = treeNode.count
        treeNode = treeNode.nodeLink
    return condPats


# 递归查找频繁项集
# 参 freqItemList 返回频繁项集列表
def mineTree(inTree, headerTable, minSup, preFix, freqItemList):
    # 头指针按其元素项出现的频率从小到大进行排序
    bigL = [v[0] for v in sorted(headerTable.items(), key=lambda p: p[1])]

    for basePat in bigL:  #start from bottom of header table
        newFreqSet = preFix.copy()   # 生成一个频繁项集
        newFreqSet.add(basePat)

        # 创造条件基
        freqItemList.append(newFreqSet)  # 繁频项集添加到参数中, 以待最后返回
        condPattBases = findPrefixPath(basePat, headerTable[basePat][1])

        # 创建条件 FP 树
        myCondTree, myHead = createTree(condPattBases, minSup)

        # 递归挖掘条件 FP 树
        if myHead != None:
            mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList)


# 载入数据
def loadSimpDat():
    simpDat = [['r', 'z', 'h', 'j', 'p'],
               ['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],
               ['z'],
               ['r', 'x', 'n', 'o', 's'],
               ['y', 'r', 'x', 'z', 'q', 't', 'p'],
               ['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]
    return simpDat


# 初始化每个项集的次数为 1
def createInitSet(dataSet):
    retDict = {}
    for trans in dataSet:
        retDict[frozenset(trans)] = 1
    return retDict


if __name__ == "__main__":
    # 建树
    simpDat = loadSimpDat()
    initSet = createInitSet(simpDat)
    myFPtree, myHeaderTab = createTree(initSet, 3)          # 3 为最小支持度
    myFPtree.disp()  # 显示树

    # 根据树挖掘 频繁项集
    freqItems = []
    mineTree(myFPtree, myHeaderTab, 3, set([]), freqItems)  # 3 为最小支持度
    print freqItems

说明
本文为《Machine Leaning in Action》第十二章(Efficiently finding frequent itemsets with FP-growth)读书笔记, 代码稍作修改及注释. 

好文参考
1.《Frequent Pattern 挖掘之二(FP Growth算法)》
2.《FP-Tree算法的实现》
3.《关联挖掘算法Apriori和FP-Tree学习》