零零散散学算法之详解几种最短路径
深入解析最短路径算法
正文
第一节 问题的提出及解决方法
所谓最短路径问题,可以说有两种情况来描述。
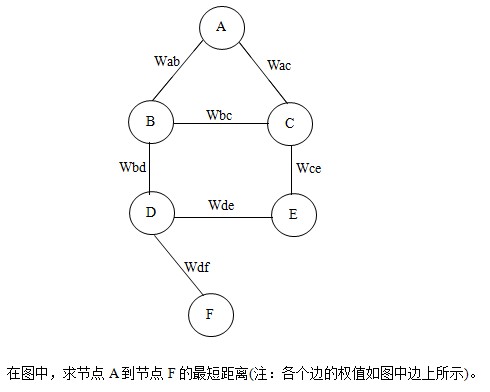
描述一:在图论中,指的是寻找图中两个节点之间的最短距离。如下图
第一节 问题的提出及解决方法
所谓最短路径问题,可以说有两种情况来描述。
描述一:在图论中,指的是寻找图中两个节点之间的最短距离。如下图

描述二:在现实生活中,指的是找到从一个地方到另一个地方的最近距离。如下图


上述两种情况的本质是一样的,即求一个点到另一个点的最短路径。好了,问题已经提出来了,那怎么解决呢?解决该问题的方法还是比较多的,不过由于各个路径算法所对应的问题条件不同,我们可根据不同的情况,选择不同的路径算法。
本文将介绍三种最短路径算法,分别是:戴克斯特拉算法(Dijkstra algorithm),弗洛伊德算法(Floyd algorithm)以及A*搜索算法。
第二节 戴克斯特拉算法(Dijkstra algorithm)
该算法解决的是有向图中单个源点到其他顶点的最短路径问题。
戴克斯特拉算法的实现过程如下:
第一步:用带权的矩阵WeiArcs来表示带权有向图,如果图中的两个顶点vi和vj是连通的,则用WeiArcs[i][j]表示这两个顶点所形成边的权值;如果vi和vj不连通,即<vi,vj>这条边不存在,那么将WeiArcs[i][j]置为∞。
第二步:设S为已求得的从某一顶点v始发的最短路径的终点的集合,且S的初始状态为空,初始化时,将始发顶点置于S集合中。那么从v出发到图中其余各个顶点vi可能达到的最短路径长度的初值为D[i]。
第三步:选择一顶点vj,使得vj就是当前求得的一条从顶点v出发的最短路径的终点。此时令S = S ∪ {vj}。
第四步:修改从v出发到集合V-S(V为图顶点的集合)中任一顶点vk可达的最短路径长度。如果D[j]+WeiArcs[j][k] < D[K],则D[k] = D[j] + WeiArcs[j][k]。
第五步:重复操作第三步、第四步共N-1次,由此就能求得从v出发到图中其余各个顶点的最短路径。
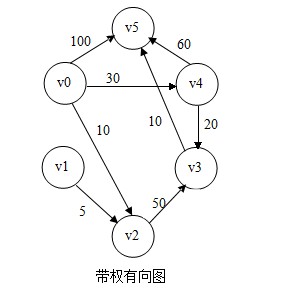
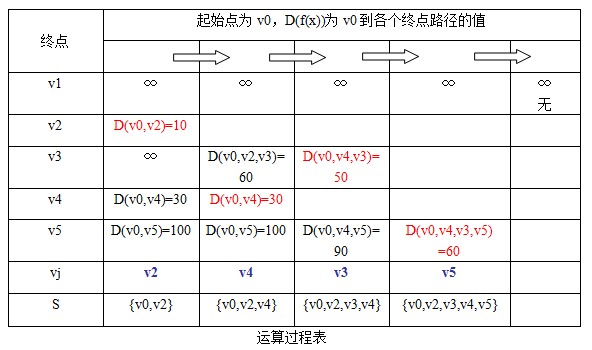
好了,实现过程就是这样。不过光有文字描述不行,要更直白的表达这个过程,我认为用图像表述是一个很好的选择。如下图所示

本文将介绍三种最短路径算法,分别是:戴克斯特拉算法(Dijkstra algorithm),弗洛伊德算法(Floyd algorithm)以及A*搜索算法。
第二节 戴克斯特拉算法(Dijkstra algorithm)
该算法解决的是有向图中单个源点到其他顶点的最短路径问题。
戴克斯特拉算法的实现过程如下:
第一步:用带权的矩阵WeiArcs来表示带权有向图,如果图中的两个顶点vi和vj是连通的,则用WeiArcs[i][j]表示这两个顶点所形成边的权值;如果vi和vj不连通,即<vi,vj>这条边不存在,那么将WeiArcs[i][j]置为∞。
第二步:设S为已求得的从某一顶点v始发的最短路径的终点的集合,且S的初始状态为空,初始化时,将始发顶点置于S集合中。那么从v出发到图中其余各个顶点vi可能达到的最短路径长度的初值为D[i]。
第三步:选择一顶点vj,使得vj就是当前求得的一条从顶点v出发的最短路径的终点。此时令S = S ∪ {vj}。
第四步:修改从v出发到集合V-S(V为图顶点的集合)中任一顶点vk可达的最短路径长度。如果D[j]+WeiArcs[j][k] < D[K],则D[k] = D[j] + WeiArcs[j][k]。
第五步:重复操作第三步、第四步共N-1次,由此就能求得从v出发到图中其余各个顶点的最短路径。
好了,实现过程就是这样。不过光有文字描述不行,要更直白的表达这个过程,我认为用图像表述是一个很好的选择。如下图所示



从运算过程表中,我们可知v0到其余个点的最短路径,如下图



上述过程描述的戴克斯特拉算法的代码如下:
第三节 弗洛伊德算法(Floyd algorithm)
该算法解决的是有向带权图中两顶点之间最短路径的问题。
弗洛伊德算法的设计过程如下:
用带权的矩阵WeiArcs来表示带权有向图,如果图中的两个顶点vi和vj是连通的,则用WeiArcs[i][j]表示这两个顶点所形成边的权值;如果vi和vj不连通,即<vi,vj>这条边不存在,那么将WeiArcs[i][j]置为∞。
要求:求节点vi到节点vj的最短路径。
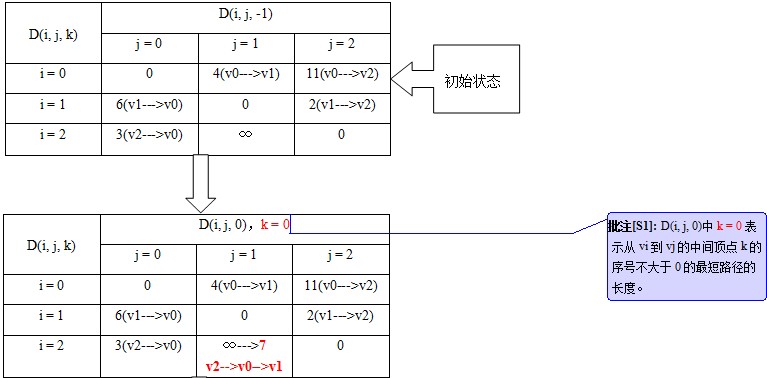
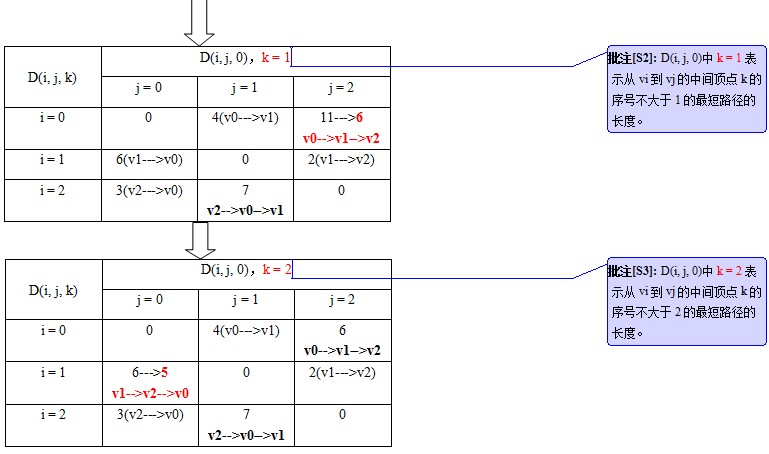
设D(i,j,k)为从节点vi到节点vj的以vk(vk∈(0,1,...k))节点为中间节点的最短路径的长度。例如:从vi到vj这条路径上经过节点vm和节点vk,那么可表示为:vi-->vm-->vk-->vj。
那么,就有:1.若最短路径经过节点vk,则D(i,j,k) = D(i,k,k-1) + D(k,j,k-1);
2.若最短路径不经过节点vk,则D(i,j,k) = D(i,j,k-1)。
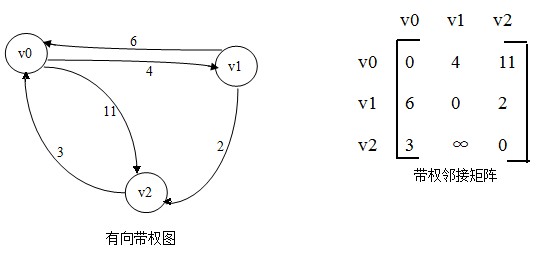
所以,求的vi到vj的最短路径可表示为:
int ShortPath(MGraph G,int v0,PathMatrix &P,ShortPathTable &D) { //用戴克斯特拉算法求有向图G中v0顶点到其余顶点v的最短路径P[v]及带权长度D[v]。 //若P[v][w]为TRUE,则w是从v0到v当前求得最短路径上的顶点。 //final[v]为TRUE当且仅当v∈S,即已经求得从v0到v的最短路径。 for(v = 0;v < G.vexmun;v++) { final[v] = FALSE; D[v] = G.WeiArcs[v0][v]; for(w = 0;w < G.vexnum;w++) P[v][w] = FALSE; //设空路径 if(D[v] < INFINITY) { p[v][v0] = TRUE; p[v][v] = TRUE; } } D[v0] = 0;final[v0] = TRUE; //初始化,v0顶点属于S集合 //开始主循环,每次求得v0到某个顶点v的最短路径,并将v加到S集合中 for(i = 1; i < G.vexnum; i++) //其余G.vexnum - 1个顶点 { min = INFINITY; //当前所知离v0点的最近距离 for(w = 0;w < G.vexnum; i++) { if(!final[w]) //w顶点在V - S中 { if(D[w] < min) //w顶点离v0更近 { v = w; min = D[w]; } } } final[v] = TRUE; //离v0顶点最近的v加入到S中 for(w = 0;w < G.vexnum;w++) //更新当前最算路径及距离 { if(!final[w] && (min + G.WeiArcs < D[w])) { D[w] = min + G.WeiArcs[v][w]; //p[w] = P[v] + P[w]; P[w] = P[v]; P[w][w] = TRUE; } } } return 0; }
ok,Dijkstra algorithm介绍完了。
第三节 弗洛伊德算法(Floyd algorithm)
该算法解决的是有向带权图中两顶点之间最短路径的问题。
弗洛伊德算法的设计过程如下:
用带权的矩阵WeiArcs来表示带权有向图,如果图中的两个顶点vi和vj是连通的,则用WeiArcs[i][j]表示这两个顶点所形成边的权值;如果vi和vj不连通,即<vi,vj>这条边不存在,那么将WeiArcs[i][j]置为∞。
要求:求节点vi到节点vj的最短路径。
设D(i,j,k)为从节点vi到节点vj的以vk(vk∈(0,1,...k))节点为中间节点的最短路径的长度。例如:从vi到vj这条路径上经过节点vm和节点vk,那么可表示为:vi-->vm-->vk-->vj。
那么,就有:1.若最短路径经过节点vk,则D(i,j,k) = D(i,k,k-1) + D(k,j,k-1);
2.若最短路径不经过节点vk,则D(i,j,k) = D(i,j,k-1)。
所以,求的vi到vj的最短路径可表示为:
D(i,j,k) = min(D(i,k,k-1) + D(k,j,k-1), D(i,j,k-1))。
老办法,图示的过程如下:
求解的过程见下图:


上述过程描述的弗洛伊德算法的代码如下:
第四节 A*搜索算法
A*搜索算法,俗称A星算法。这是一种在图平面上,有多个节点的路径,求出最低通过成本的算法。常用于游戏中的NPC的移动计算,或线上游戏的BOT的移动计算上。该算法像Dijkstra算法一样,可以找到一条最短路径;也像BFS一样,进行启发式的搜索。
A*算法最核心的部分,就在于它的一个估值函数的设计上:f(n)=g(n)+h(n)。其中,g(n)表示从起始点到任一点n的实际距离,h(n)表示任意顶点n到目标顶点的估算距离,f(n)是每个可能试探点的估值。这个估值函数遵循以下特性:
int ShortPath(MGraph G,int v0,PathMatrix &P,ShortPathTable &D) { //用Floyd算法求有向图中各对顶点v和w之间的最短路径P[v][w]及其带权长度D[v][w]。 //若p[v][w][u]为TRUE,则u是从v到w当前求得的最短路径上的顶点 for(v = 0;v < G.vexnum;v++) for(w = 0;w < G.vexnum;w++) { D[v][w] = G.arcs[v][w]; if(D[v][w] < INFINITY) //从v到w有直接路径 { P[v][w][u] = TRUE; P[v][w][w] = TRUE; } } for(u = 0;u < G.vexnum;u++) for(v = 0;v < G.vexnum;v++) for(w = 0;w < G.vexnum;w++) { if(D[v][u] + D[u][w] < D[v][w]) //从v经u到w的一条更短路径 D[v][w] = D[v][u] < D[u][w]; for(i = 0;i < G.vexnum;i++) P[v][w][i] = P[v][u][i] || P[u][w][i]; } return 0; }
第四节 A*搜索算法
A*搜索算法,俗称A星算法。这是一种在图平面上,有多个节点的路径,求出最低通过成本的算法。常用于游戏中的NPC的移动计算,或线上游戏的BOT的移动计算上。该算法像Dijkstra算法一样,可以找到一条最短路径;也像BFS一样,进行启发式的搜索。
A*算法最核心的部分,就在于它的一个估值函数的设计上:f(n)=g(n)+h(n)。其中,g(n)表示从起始点到任一点n的实际距离,h(n)表示任意顶点n到目标顶点的估算距离,f(n)是每个可能试探点的估值。这个估值函数遵循以下特性:
 |
 |
|
0人
|
了这篇文章 |
类别: Algorithm Field┆阅读(
0)┆评论(
0) ┆ 返回博主首页┆ 返回博客首页
上一篇 最大流问题:增广路径算法的比较之序 下一篇 由n阶幻方问题引发的思考
文章评论
发表评论
- 昵 称:
- 登录 快速注册
- 验证码:
-
点击图片可刷新验证码请点击后输入验证码博客过2级,无需填写验证码
- 内 容:
同时赞一个

每日博报 精彩不止一点


