MATLAB入门基础

预定义变量

>> format short e
>> RMAd = realmax('double')  %双精度类型默认最大实数

RMAd =

  1.7977e+308

>> RMAs = realmax('single')  %单精度类型最大实数

RMAs =

  3.4028e+38
>> IMA64 = intmax('int64')   %int64整数类型最大正整数

IMA64 =

  9223372036854775807

>> IMA32 = intmax   %int32整数类型最大正整数

IMA32 =

  2147483647

>> IMA32 = intmax('int16') %int16整数类型最大正整数

IMA32 =

  32767
>> e1 =eps %双精度类型相对精度

e1 =

   2.2204e-16

>> e2 = eps(2) %表达2时的相对精度

e2 =

   4.4409e-16  
>> pi

ans =

   3.1416e+00

面向复数设计的运算

>> z3 = 2*exp(i*pi/6);%运算符构成的极坐标表示法
>> z1 = 4+3i;%运算符构成的直角坐标表示法
>> z2 = 1+2*i;
>> z = z1*z2/z3;
>> z1

z1 =

   4.0000e+00 + 3.0000e+00i

>> z2

z2 =

   1.0000e+00 + 2.0000e+00i

>> z3

z3 =

   1.7321e+00 + 1.0000e+00i

>> z

z =

   1.8840e+00 + 5.2631e+00i

>> real_z = real(z)

real_z =

   1.8840e+00

>> image_z=imag(z)

image_z =

   5.2631e+00

>> magnitude_z = abs(z)

magnitude_z =

   5.5902e+00

>> angle_z_radian = angle(z)%弧度单位

angle_z_radian =

   1.2271e+00

>> angle_z_degree = angle(z)*180/pi%度数单位

angle_z_degree =

   7.0305e+01
>> z1 = 4+3*i; %指令后采用分号，使得运算结果不显示
>> z2= 1+2*i;
>> z12 = z1+z2;
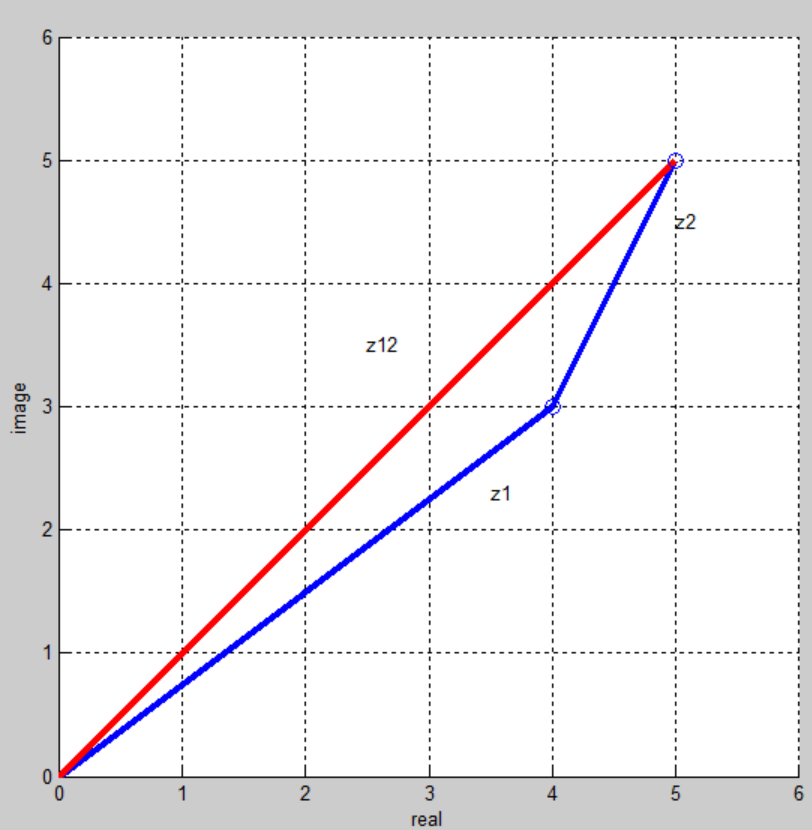
>> clf,hold on %clf清空图形窗口，逗号用来分隔两个指令
>> plot([0,z1,z12],'-b','LineWidth',3)
>> plot([0,z12],'-r','LineWidth',3)
>> plot([z1,z12],'ob','MarkerSize',8)
>> hold off, grid on
>> axis equal
>> axis([0,6,0,6])
>> text(3.5,2.3,'z1')
>> text(5,4.5,'z2')
>> text(2.5,3.5,'z12')
>> xlabel('real')
>> ylabel('image')
>> shg

求一个数的3次方根

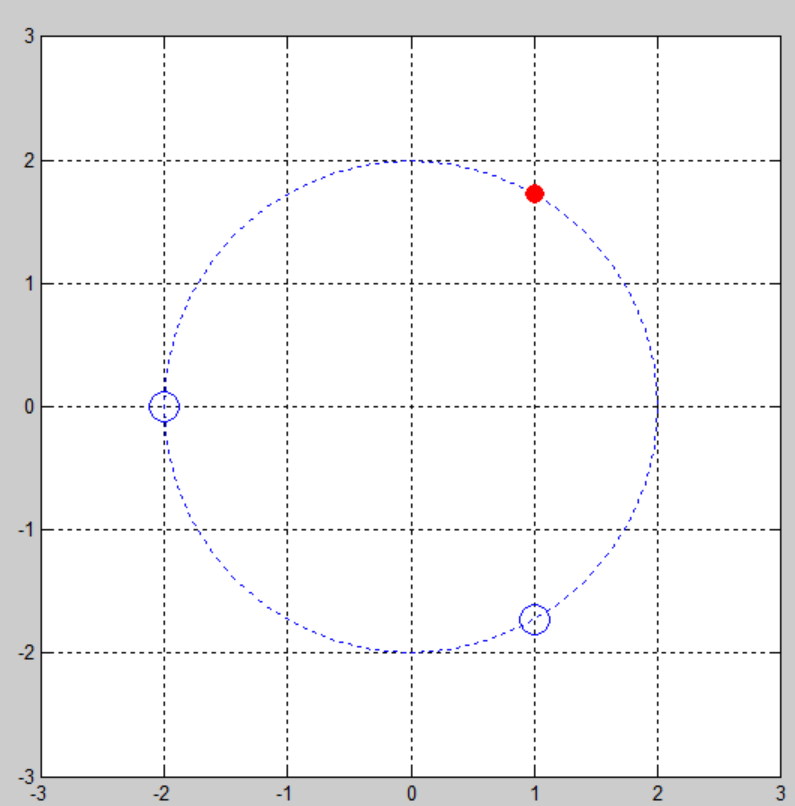
>> a = -8;
>> r_a = a^(1/3)

r_a =

   1.0000e+00 + 1.7321e+00i

>> p=[1,0,0,-a];%先构建一个多项式p(r)=r^3-a,p是多项式的系数向量
                %指令末尾的英文状态分号使得该指令运行后不显示结果
>> R = roots(p)

R =

  -2.0000e+00 + 0.0000e+00i
   1.0000e+00 + 1.7321e+00i
   1.0000e+00 - 1.7321e+00i
>>  t = 0:pi/20:2*pi;
>>  MR = abs(R(1))%计算复数根的模
>> x = MR*sin(t);
>> y = MR*cos(t);
>>  plot(x,y,'b:'),grid on
>>  hold on
>>  plot(R(2),'.','MarkerSize',30,'Color','r')
>>  plot(R([1,3]),'o','MarkerSize',15,'Color','b')
>> axis([-3,3,-3,3]),axis square %保证屏幕显示真圆
>> hold off

面向数组设计的运算

>> AR = [1,3;2,4]

AR =

     1     3
     2     4
>> AI = [5,7    %回车用来分隔数组中的行
6,8]

AI =

     5     7
     6     8    
>> AR = [1,3;2,4];
>> AI = [5,7;6,8];
>> A = AR - AI*i
A =
   1.0000 - 5.0000i   3.0000 - 7.0000i
   2.0000 - 6.0000i   4.0000 - 8.0000i
>> A_real = real(A)
A_real =
     1     3
     2     4
>> A_image = imag(A)
A_image =
    -5    -7
    -6    -8 
>> for m =1:2 %循环法计算复数矩阵中各个元素的模和幅角
for n = 1:2
Am1(m,n)= abs(A(m,n));
Aa1(m,n) = angle(A(m,n))*180/pi;
end
end
>> Am2 = abs(A)%直接法求复数矩阵的各个元素的模和幅角
Am2 =
    5.0990    7.6158
    6.3246    8.9443
>> Aa2 = angle(A)*180/pi
Aa2 =
  -78.6901  -66.8014
  -71.5651  -63.4349

real,imag,abs,angle是同时、并行作用于数组的每个元素的，对4个元素的运算所需的时间大致与对单个元素所需的时间相同。这有利于运行速度的提高。这是向量化运算的一种形式。循环法求各个元素的模和幅角的指令不是很有效的计算方法。对于MATLAB之外的许多编程语言来说，应该尽量摒弃循环处理，采用向量化的处理方式。

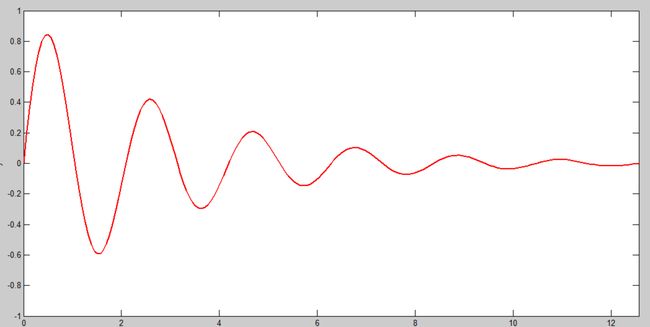
对于衰减振荡曲线y = e^(-t/3)*sin(3t),t= [0,4pi]

>> t = 0:pi/50:4*pi;%定义自变量t的取值数组
>> y = exp(-t/3).*sin(3*t);%计算与自变量相应的y数组，注意乘法运算符前面的小黑点
>> plot(t,y,'-r','LineWidth',2)%绘制曲线
>> axis([0,4*pi,-1,1])
>> xlabel('t'),ylabel('y')

.*符号表示的是在两个数组的相同位置上的元素之间进行的乘法运算。即“数组乘”。数组乘的引入不但使得程序显得简洁自然，而且避免了耗费机器时间的循环运算。应当尽可能的像第二条指令那样采用“向量化”的运算形式。

>> B = [3+2i,2+6i;5+3*i,4-2*i]%复数数组的输入方式
B =
   3.0000 + 2.0000i   2.0000 + 6.0000i
   5.0000 + 3.0000i   4.0000 - 2.0000i
>> C = A * B                  %矩阵乘法
C =
  49.0000 -39.0000i  30.0000 -38.0000i
  62.0000 -42.0000i  40.0000 -40.0000i

当数组具备变换的属性时，二维数组就被称为矩阵。当两个矩阵的“内维大小相等”时，矩阵乘法才能进行。矩阵A的列数和矩阵B的行数相等，所以可以进行A乘以B的运算。在MATLAB中，矩阵相乘和标量相乘的格式一样，而在其他的编程语言中，矩阵的乘法不得不依赖循环进行。MATLAB的设计者之所以能够把矩阵运算表达的像“线性代数”那样简洁易读，自然流畅，是因为MATLAB设计者采用了“面向对象”的编程技术。