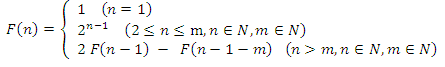博文视点答题<1>

博文视点答题

1. 二维数组中的查找
1.1. 问题描述
    在一个二维整数数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。
     例如下面的二维数组就是每行、每列都递增排序。如果在这个数组中查找数字7，则返回true；如果查找数字5，由于数组不含有该数字，则返回false。

图1-1

1.2. 问题分析
    由于数组M是一个m*n阶矩阵。矩阵M的可能情况如下：

矩阵M的特点是：
(1) 图中“ 红色元素”是以第一个元素为顶点的最大正方形对角线上的元素，这条对角线上的红色元素把矩阵的每行和每列都切割成了两部分。
(2) 行和列都是递增数列，“红色元素”所在行的左侧都比它小，右侧都比它大；所在列的上侧都比它小，下侧都比它大。
(3)矩阵M的第一个元素最小，最后一个元素最大。

算法描述：
    (1)将key分别与矩阵的最大元素和最小元素比较，如果key比矩阵的最大元素大或者比最小元素小，则无须继续查找，不存在这样的key。
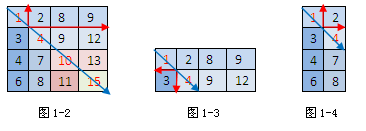
    (2)以“红色元素”为分割点，对于行数大于等于列数的矩阵采用 列二分搜索(如图1-2和图1-4所示矩阵)。如果key等于“红色元素”返回true；比“红色元素”大在列下侧搜索；比“红色元素”小，则key只可能在图中红色箭头围成的区域中，把这样的区域称为“ 最小区域”。发现“最小区域”后，直接进入最小区域搜索。
    (3)对于行数小于列数的矩阵采用 行二分搜索(如图1-3所示矩阵)。

1.3. 算法实现
1.3.1. 行搜索算法

boolean rowSearch(int [][] matrix,int key) {
	int row = matrix.length-1,col = matrix[0].length-1;
	int low = 0 , high = 0,mid = 0,midVal = 0,fixMin=-1;
	for (int i = 0; i <= row ; i++) {
		if(fixMin != -1) {
			low = 0;
			high = fixMin;
		} else {
			if(key > matrix[i][i]) {
				low = i+1;
				high = col;	 
			} else if(key < matrix[i][i]) {
				low = 0;
				high = i-1;
				fixMin = high;//发现最小区域
			} else {
				return true;
			}	
		}
		while(low <= high) {
			mid = (low + high)>>1;
			midVal = matrix[i][mid];
			if(key < midVal) {
				high = mid -1;
			} else if (key > midVal) {
				low = mid + 1;
			} else {
				return true;//发现key
			}
		}						
	}
	return false;//没有发现key
}

1.3.2. 列搜索算法

boolean colSearch(int [][] matrix,int key) {
	int row = matrix.length-1,col = matrix[0].length-1;
	int low = 0 , high = 0,mid = 0,midVal = 0,fixMin=-1;
	for (int i = 0; i <= col ; i++) {
		if(fixMin != -1) {
			low = 0;
			high = fixMin;
		} else {
			if(key > matrix[i][i]) {
				low = i+1;
				high = row;	 
			} else if(key < matrix[i][i]) {
				low = 0;
				high = i-1;
				fixMin = high;//发现最小区域
			} else {
				return true;
			}	
		}
		while(low <= high) {
			mid = (low + high)>>1;
			midVal = matrix[mid][i];
			if(key < midVal) {
				high = mid -1;
			} else if (key > midVal) {
				low = mid + 1;
			} else {
				return true;//发现key
			}
		}					
	}
	return false;//没有发现key
}

1.3.3. 搜索主算法

boolean search(int [][] matrix,int key) {
	//比最小值小
	if(key<matrix[0][0]) {
		return false ;
	}
	int row = matrix.length-1,col = matrix[0].length-1;
	//比最大值大
	if(key > matrix[row][col]) {
		return false ;
	}
	if( row < col) {
		//行数小于列数采用行搜索
		return rowSearch(matrix, key);
	} else {
		//行数大于等于列数采用列搜索
		return colSearch(matrix, key);
	}
}

2. 青蛙跳台阶问题
2.1. 问题描述
    (1) 一只青蛙一次可以跳上 1 级台阶，也可以跳上2 级。求该青蛙跳上一个n 级的台阶总共有多少种跳法？(2)一只青蛙一次可以跳上1级台阶，也可以跳上2 级……它也可以跳上n 级，此时该青蛙跳上一个n级的台阶总共有多少种跳法？

2.2. 问题分析
    对于n步台阶，记青蛙的跳法为F(n),n=S1+S2(其中Si表示一次连跳i步的次数.
当n=1时,(1,0) →F(n) = 1;
当n=2时,(0,1),(2,0) →F(n) = 2;
当n=3时,(1,1)[2], (3,0) →F(n) = 3;
     青蛙可以先跳一步，再跳一次两连步；或者先跳一次两连步，再跳一次一步，故共计3次。
当n=4时,(0,2),(2,1)[3], (4,0) →F(n) = 5;
由上面的推到可知：
F(1) = 1; F(2) = 2;
F(3) = F(1) + F(2) = 1+2 = 3;
F(4) = F(2) + F(3) = 2+3 = 5;
.......
假设青蛙最后一次跳1步，则青蛙的跳法与只有n-1步台阶时跳法数一致，即有F(n-1) 种跳法；
假设最后一次跳2步，则青蛙的跳法与只有n-2步台阶时跳法数一致，即有
F(n-2) 种跳法。这里实际存在 对偶关系：m+(n-m) = n ,则F(m)= F(n-m)。所以，F(n)= F(n-1) + F(n-2)。
则：

由此可见青蛙的跳法是一个 斐波那契数列。
    如果青蛙有m种跳法，即青蛙可以一次连跳1,2,3,4,5,...m阶台阶。由上面的推理过程得到:F(n)= F(n-1) + F(n-2)+...+ F(n-m).
如果 n-m < 0, F(n-m) = 0,青蛙一次能够跳跃的步数m大于台阶数n时，这样的跳法实际不存在。所以当n<m时，让m等于n。
n-m = 0, F(n-m) = 1, 即 F(0) = 1，表示青蛙一次能够跳n步台阶。
n-m = 1, F(n-m) = 1, 即 F(1) = 1。表示青蛙先跳一次再连跳m次。
对n >= 2时，对F(n)进行简化如下：
F(n-1)= F(n-2) + F(n-3)+...+ F(n-1-m).
F(n)- F(n-1) =  F(n-1)- F(n-1-m).
则F(n)=2 F(n-1) -  F(n-1-m).
当n <= m时，n – 1 – m < 0,F(n-1-m) = 0,则F(n)=2 F(n-1)。
F(1) = 1; F(2) = 2; F(3) = 4;…;F(n)=2^(n-1)。则：

2.3. 算法实现
2.3.1.1. 问题一的递归算法

int jump2(int n) {
	if(n == 1 || n == 2) {
		return n;
	}
    return jump2(n-1)+jump2(n-2);
}

2.3.1.2. 问题一的非递归算法

int jump2(int n) {
 	if(n == 1 || n == 2) {
		return n;
	}
	int n1 = 1,n2 = 2;
	int r = 0;
	for (int i = 3; i <= n; i++) {
		r = n1 + n2 ;
		n1 = n2;
		n2 = r ;
	}
	return r;
}

2.3.2.1. 问题二的递归算法

int jumpm0(int n,int m) {
	if(n == 0) {
		return 1;
	}
	if(n <= m) {
		return 1<<(n-1);
	}
	return 2*jumpm0(n-1,m)-jumpm0(n-1-m,m);
}

2.3.3.2. 问题二的非递归算法

int jumpm(int n,int m) {
	if(n <= m) {
		return 1<<(n-1);
	}
	int [] f = new int [1 + m];
	f[0] = 1;
	//求f[1]...f[m]
	for (int i = 0; i < m; ) {
		f[++i] = 1<<i;
	}
	//求fn
	int r = f[m];
	for (int i = m+1; i < n;i++) {
		r = 2 * f[m] - f[0];
		f = poll(f);
		f[m] = r;
	}
	r = 2 * f[m] - f[0];
	return r;
}

int [] poll( int [] m) {
	int len = m.length-1;
	for (int i = 0; i < len ;) {
		m[i] = m[++i];
	}
	return m;
}

图2-1

     非递归算法通过增加辅助存储空间来存储F(n-1-m),.., F(n-2), F(n-1)。首先通过公式F(n)= F(n-1) + F(n-2)+...+ F(n-m)。求出F(0),…, F(1), F(m)。然后通过迭代求F(n)。迭代过程中通过公式F(n)=2 F(n-1) -  F(n-1-m)，求F(n)。每次迭代都需要像图2-1那样移动元素。

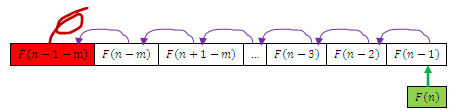
2.3.3.3. 问题二的非递归算法的改进
    问题二的非递归算法中，求F(n)的迭代过程中用到了poll函数，这样每迭代一次数组f都需要整体向做移动一次，效率比较低。如果把数组f中的元素存到一个队列中，每次迭代实际上只与第一个元素和最后一个元素有关。迭代过程中移除首元素之后取出其值和最后一个元素的值计算出F(i)。再将F(i)插入到队尾。这样减少了数组的移动，提高了效率。但需要消耗一定的空间创建对象实例。以空间换取效率。改进后的 存储模型如下：

图2-2

    改进后的java代码如下：

int jumpmm(int n,int m) {
	if(n <= m) {
		return 1<<(n-1);
	}
	//将f[0]...f[m]存放到队列中
	Deque<Integer> fq = new LinkedList<Integer>();
	fq.add(Integer.valueOf(1));
	for (int i = 0; i < m; i++) {
		fq.add(Integer.valueOf(1<<i));
	}
	//求fn
	int r = 0;
	for (int i = m+1; i < n;i++) {
		r = 2 * fq.peekLast() - fq.pollFirst();
		fq.add(Integer.valueOf(r));
	}
	r = 2 * fq.peekLast() - fq.pollFirst();
	return r;
}

2.3.3.4. 问题二的运行结果

图2-3

3. 总结
    通过本文可以了解 二分查找算法的实现； 递归算法向 迭代转化的方法；问题的 分析和推演方法；同时还可以了解java中队列的使用方法。在实际问题中 针对问题本身的特征对问题进行分析是一条很重要的法则，仔细阅读本文就可以看到本文的分析与算法都是基于问题本身的特征的。

4. 附件
    附件中有本文的word，pdf详细文档和java代码。
    附件《ch02.pdf》有第一题的一种巧妙解法。供大家学习参考。在pdf的第19页。