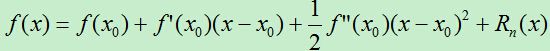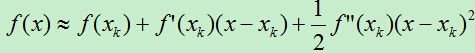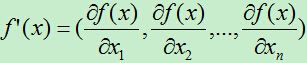牛顿法
牛顿法法主要是为了解决非线性优化问题,其收敛速度比梯度下降速度更快。其需要解决的问题可以描述为:对于目标函数f(x),在无约束条件的情况下求它的最小值。
其中x=(x1,x2,..,xn)是n维空间的向量。我们在下面需要用到的泰勒公式先在这写出来。
牛顿法的主要思想是:在现有的极小值估计值的附近对f(x)做二阶泰勒展开,进而找到极小点的下一个估计值,反复迭代直到函数的一阶导数小于某个接近0的阀值。
为了便于理解,我们通常先从简单的开始进行分析,于是我们就先从x的维度n=1时开始进行讨论。
1)n=1时。
设x=xt时,函数f(x)取得最小值,我们的目标就是希望能求得xt,现在我们设xk作为xt的估计值。首先我们在x=xk处进行泰勒二阶展开,得:
然后对f(x)求导,得:
令:![]() ,即:
,即:
![]()
所以有:
若从初始值x=x0开始进行迭代,将得到x的一个序列:x0,x1,…xk。在一定条件下,此序列可以收敛到f(x)的极小值点。
2)n>1时。
此时,可以将x写成:x=(x1,x2,…,xn)。同样,我们先对x进行泰勒展开:
然后对f(x)求导,此处的求导比n=1的情形要复杂一点,由于f(x)中的x是一个向量,f(x)对x求导意味着对x向量中的每个值求偏导。即,f(x)对x的一阶导数为一个向量,对x的二阶导数为一个n*n的矩阵。
求导后得:
为了方便表达,我们令:
![]()
此时的gk为一个向量,Hk为一个矩阵。
我们令(式1.1)中的f(x)导数为0,得:
即:
![]()
所以:
得到x的迭代值为:
牛顿法算法流程:
1)初始化x0,设置终止阀值a,令k=0.
2)计算f(x)在x=xk的梯度向量gk和海塞矩阵Hk-1的逆矩阵,其计算公式为:
3)判断||gk||<a,则停止计算,得到x=xk即为所求。
算法分析:
1)前提:
要使用该算法要满足两个条件:一是函数f(x)一阶,二阶可偏导;二是海塞矩阵要求正定。若要使得最终结果能收敛到最小值,则f(x)需要为凸函数。
当f(x)满足: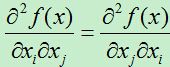 时,海塞矩阵为对称矩阵,对所有特征值大于0的对称矩阵称为正定矩阵。正定矩阵一定是非奇异矩阵。
时,海塞矩阵为对称矩阵,对所有特征值大于0的对称矩阵称为正定矩阵。正定矩阵一定是非奇异矩阵。
附:若A为奇异矩阵,则有:|A|=0.
2)优点:
它比传统的梯度下降算法收敛速度明显要快,另外,当f(x)是二次函数时,仅需一次迭代就能直接收敛到最小值。因为f(x)为二次函数时,在进行泰勒展开式,并没有高阶导数的损失,而在后面的每次计算都是等号运算,因而最后得到结果就是函数f(x)最小值对应的x。而对于非二次函数,若函数的二次形态较强,或迭代点已进入极小点的领域内,则其收敛速度也会很快。
3)缺点:
A)计算复杂度问题。
在上面的这个算法中存在一个问题,即海塞矩阵的计算问题,此问题需要对f(x)求二阶偏导数,计算开销很大;另一方面,海塞矩阵的大小是n的平方,当n增大时,存储和计算的量是平方的速度增加。
针对计算复杂度问题,于是有了拟牛顿法。
B)收敛性问题。
对于非二次函数,也可能会出现f(xk+1)>f(xk)的情况,这时,牛顿法不能收敛,从而导致计算失败。对于这种情况,可以使用阻尼牛顿法来解决。
阻尼牛顿法最核心的一点在于可以修改每次迭代的步长,通过沿着牛顿法确定的方向一维搜索最优的步长,最终选择使得函数值最小的步长。
关于步长的搜索,主要有精确搜索和非精确搜索,上面的方法是一种精确地搜索方法,在实际中还有Wolfe型搜索,Armijo搜索以及满足Goldstein条件的非精度搜索。具体的搜索方法大家可自行研究。
参考文献:
[1] peghoty, http://blog.csdn.net/itplus/article/details/21896453
[2]李航,统计学习方法。