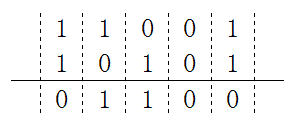【数据校验杂谈】循环冗余检验 (CRC) 算法原理
循环冗余检验 (CRC) 算法原理
Cyclic Redundancy Check循环冗余检验,是基于数据计算一组效验码,用于核对数据传输过程中是否被更改或传输错误。
算法原理
假设数据传输过程中需要发送15位的二进制信息g=101001110100001,这串二进制码可表示为代数多项式g(x) = x^14 + x^12 + x^9 + x^8 + x^7 + x^5 + 1,其中g中第k位的值,对应g(x)中x^k的系数。将g(x)乘以x^m,既将g后加m个0,然后除以m阶多项式h(x),得到的(m-1)阶余项r(x)对应的二进制码r就是CRC编码。
h(x)可以自由选择或者使用国际通行标准,一般按照h(x)的阶数m,将CRC算法称为CRC-m,比如CRC-32、CRC-64等。国际通行标准可以参看http://en.wikipedia.org/wiki/Cyclic_redundancy_check
g(x)和h(x)的除运算,可以通过g和h做xor(异或)运算。比如将11001与10101做xor运算:
明白了xor运算法则后,举一个例子使用CRC-8算法求101001110100001的效验码。CRC-8标准的h(x) = x^8 + x^7 + x^6 + x^4 + x^2 + 1,既h是9位的二进制串111010101。

经过迭代运算后,最终得到的r是10001100,这就是CRC效验码。
通过示例,可以发现一些规律,依据这些规律调整算法:
1. 每次迭代,根据gk的首位决定b,b是与gk进行运算的二进制码。若gk的首位是1,则b=h;若gk的首位是0,则b=0,或者跳过此次迭代,上面的例子中就是碰到0后直接跳到后面的非零位。

2. 每次迭代,gk的首位将会被移出,所以只需考虑第2位后计算即可。这样就可以舍弃h的首位,将b取h的后m位。比如CRC-8的h是111010101,b只需是11010101。
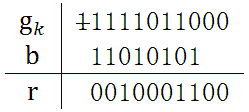
3. 每次迭代,受到影响的是gk的前m位,所以构建一个m位的寄存器S,此寄存器储存gk的前m位。每次迭代计算前先将S的首位抛弃,将寄存器左移一位,同时将g的后一位加入寄存器。若使用此种方法,计算步骤如下:

※蓝色表示寄存器S的首位,是需要移出的,b根据S的首位选择0或者h。黄色是需要移入寄存器的位。S'是经过位移后的S。
查表法
同样是上面的那个例子,将数据按每4位组成1个block,这样g就被分成6个block。
下面的表展示了4次迭代计算步骤,灰色背景的位是保存在寄存器中的。

经4次迭代,B1被移出寄存器。被移出的部分,不我们关心的,我们关心的是这4次迭代对B2和B3产生了什么影响。注意表中红色的部分,先作如下定义:
B23 = 00111010
b1 = 00000000
b2 = 01010100
b3 = 10101010
b4 = 11010101
b' = b1 xor b2 xor b3 xor b4
4次迭代对B2和B3来说,实际上就是让它们与b1,b2,b3,b4做了xor计算,既:
B23 xor b1 xor b2 xor b3 xor b4
可以证明xor运算满足交换律和结合律,于是:
B23 xor b1 xor b2 xor b3 xor b4 = B23 xor (b1 xor b2 xor b3 xor b4) = B23 xor b'
b1是由B1的第1位决定的,b2是由B1迭代1次后的第2位决定(既是由B1的第1和第2位决定),同理,b3和b4都是由B1决定。通过B1就可以计算出b'。另外,B1由4位组成,其一共2^4有种可能值。于是我们就可以想到一种更快捷的算法,事先将b'所有可能的值,16个值可以看成一个表;这样就可以不必进行那4次迭代,而是用B1查表得到b'值,将B1移出,B3移入,与b'计算,然后是下一次迭代。
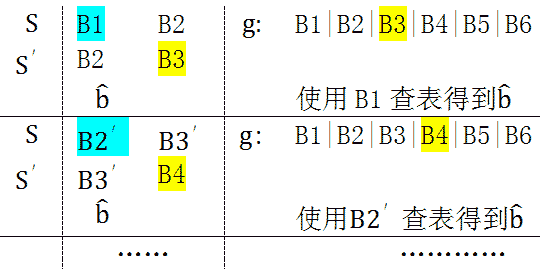
可看到每次迭代,寄存器中的数据以4位为单位移入和移出,关键是通过寄存器前4位查表获得
,这样的算法可以大大提高运算速度。
上面的方法是半字节查表法,另外还有单字节和双字节查表法,原理都是一样的——事先计算出2^8或2^16个b'的可能值,迭代中使用寄存器前8位或16位查表获得b'。
反向算法
之前讨论的算法可以称为正向CRC算法,意思是将g左边的位看作是高位,右边的位看作低位。G的右边加m个0,然后迭代计算是从高位开始,逐步将低位加入到寄存器中。在实际的数据传送过程中,是一边接收数据,一边计算CRC码,正向算法将新接收的数据看作低位。
逆向算法顾名思义就是将左边的数据看作低位,右边的数据看作高位。这样的话需要在g的左边加m个0,h也要逆向,例如正向CRC-16算法h=0x4c11db8,逆向CRC-16算法h=0xedb88320。b的选择0还是h,由寄存器中右边第1位决定,而不是左边第1位。寄存器仍旧是向左位移,就是说迭代变成从低位到高位。