深入理解计算机系统家庭作业——20135308

深入理解计算机系统家庭作业

2.74

解题思路：

有符号整数的相减，溢出规则为：

y=a-b

（1）a,b同号时，y一定不会溢出。

（2）若 a>=0 && b<0 ,则当 y<=0 时溢出。

（3）若 a<=0 && b>=0，则当y>=0时溢出。

当a != b时,  a - b 不等于0。

所以a，b异号，y，b同号即可判定为溢出。

首先先定义两个整型变量x,y，计算出他们的位数，然后计算x - y的值，将三个值右移到符号位，比较a,b是否异号，y,b是否同号。

int tsub_ovf(int x, int y)
{
    int w = sizeof(int)<<3;//左移三位相当于乘以2^3,4*8=32位
    int t = x - y;
    x>>=(w-1);//右移31位，只剩符号位
    y>>=(w-1);
    t>>=(w-1);
    return (x != y) && (y == t);
}

　

2.78

　

解题思路：

计算5*x/8相当于计算((x<<2) + x) >> 3，要舍入x为负数时的情况。

我们假设x的位模式为[b(w-1), b(w-2), ... , b(0)]

计算[b(w-1),b(w-2),b(w-3),   ...    ,b(0),  0, 0] + [b(w-1),b(w-2),...,b(2),  b(1), b(0)] ，然后右移三位，所以我们可以忽略下方的b(1),b(0)。

所以计算(x<<2) + x，再右移一位，但是(x<<2) + x可能也会溢出，所以计算(x>>3) + (x>>1)，这样就不会溢出了。看看b(0)+b(2)会不会产生进位，如果产生进位，则再加一。

最后考虑负数的舍入。负数向0舍入的条件是x<0 && ((x<<2)+x 的后三位不全为0)。满足舍入条件的话，结果再加1。加法后三位不全为0等价为x后三位不全为0。

 

int mul5div8(int x)
{
    int b0 = x&1, b2 = (x>>2)&1;
    int ans = (x>>3) + (x>>1);
    int w = sizeof(int)<<3;
    ans += (b0&b2);
    ans += ((x>>(w-1)) && (x&7));
    return ans;
} 

　　

2.90

解题思路：

A.π的二进制数表示为：0 10000000 10010010000111111101011，

它表示的二进制小数值为：11.0010010000111111101011

B.根据2.82，可知1/7的表示为0.001001[001]...，

所以22/7为11.001001001001001[001]...

C.从第9位开始不同。

8.11

 

解题思路：

4行

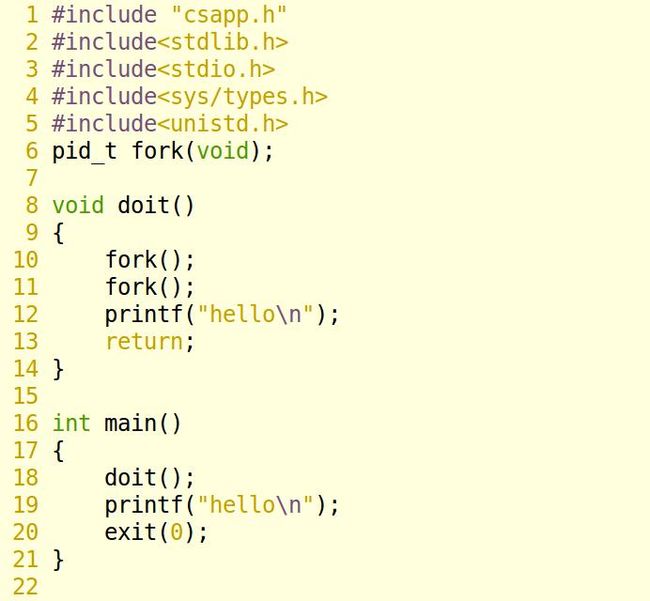
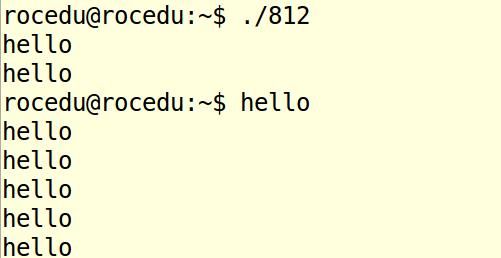
8.12

解题思路：

8行

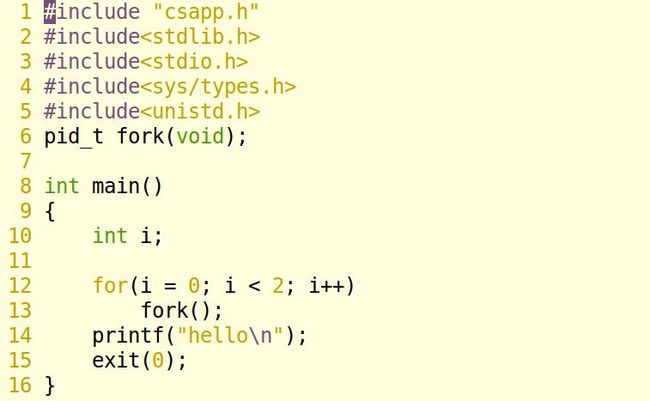
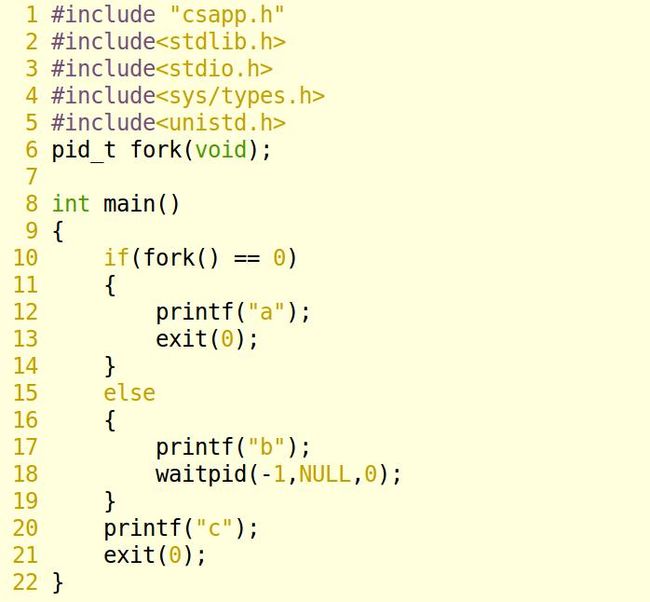
8.21

解题思路：

abc或者bac。c肯定在a和b之后。

因为fork函数只被调用一次，但是会返回两次：父进程返回子进程的PID，子进程返回0.如果失败返回-1。

在fork后，子进程和父进程继续执行fork（）函数后的指令。

所以无论是先输出a还是b，c肯定在最后面。

下面，我们调试代码，运行，验证一下结果：

将文件保存在821.c中，并调试：

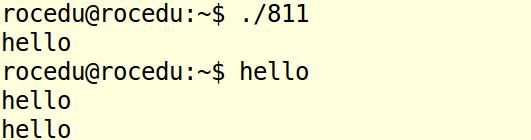
运行文件，查看结果：

结果是abc，c果然在最后面。

9.19

解题思路：

1) a是正确答案，a，对于伙伴系统，如果要申请大小为33的空间，那么需要分配64个空间。如果申请大小为65的空间，那么块大小就需要128，所以最多可能有约50%的空间被浪费。b中，最佳适配要搜索所有空间，所以肯定比首次适配要慢一些。c，边界标记主要功能是释放一个块时，能立即和前后空闲块合并。如果空闲块不按顺序排列的话，其实也能够和前一个或者后一个空闲块进行合并，但如果要和前后一起合并，可能会有些困难，那需要搜索前后块在空闲链表中的位置，并且删除一个再进行合并。可以参考P576，LIFO方法。d，其实任何分配器都可能有外部碎片，只要剩余的空闲块大小和足够但是单个都不够，就会产生外部碎片。

2)d是正确答案。d， 块大小递增，那么最佳适配法找到的块和首次适配找到的块是同一个，因为最佳适配总是想找一个刚好大于请求块大小的空闲块。a，块大小递减，首次适配很容易找到，所以分配性能会很高。b，最佳适配方法无论怎样，都要搜索所有的链表（除非维护成块大小递增的链表）。c，是匹配的最小的。

3) c是正确答案。c，保守的意思就是所有可能被引用的堆都会被标记，int像指针，所以可能认为它表示的地址是正在被引用的（实际上它只是个int）。

 

 

汇总

2.74 **

2.78 **

2.90 *

8.11 *

8.12 *

8.21 **

9.19 *

共计：十分