SVM: 实际中使用SVM的一些问题
使用SVM包来求θ,选择C与核函数
我们使用已经编写好的软件包(这些软件包效率高,用得多,是经无数人证明已经很好的可以使用的软件包)来求θ,而不是自己去编写软件来求它们(就像我们现在很少编写软件来求x½).经常使用的是liblinear和libsvm
虽然不用我们自己来写optimize函数,但是需要我们确定的是要选择C(cost function里面bias与variance权衡的参数=1/λ),以及选择什么样的kernel函数。
一种选择是不使用kernel(也称为linear kernel),直接使用x: 这种情况是当我们的n很大(即维度很高,features很多)但是训练样本却很少的情况下,我们一般不希望画出很复杂的边界线(因为样本很少,画出很复杂的边界线就会过拟合),而是用线性的边界线。
一种选择是使用Gaussian kernel: 这种情况需要确定σ2(平衡bias还是variance)。这种情况是当x的维度不高,但是样本集很多的情况下。如上图中,n=2,但是m却很多,需要一个类似于圆的边界线。(即需要一个复杂的边界)
如果features的范围差别很大,在执行kernel之前要使用feature scaling
我们需要自己编写kernel函数,当然许多SVM都包含了高斯kernel和linear kernel(因为这两个是最常见的);自己编写kernel函数时,将x1,x2(landmarks)做为输入,输出features f(f1,f2.........fm)
在使用高斯kernel时,如果features之间的范围相差太大,要先做feature scaling。因为如果不做feature scaling 的话,在求范数时,则范数主要取决于大的数值的features,而不会去关注小数值的features,这样导致不均衡。如房子价格的预测,有面积与房间个数的话,则范数主要与房子的面积相关,因为房间个数对于范数的贡献太小。
成为有效的kernels需要满足的条件以及其它的一些kernel函数
我们最常用的是高斯kernel和linear kernel(即不使用kernel),但是需要注意的是不是任何相似度函数都是有效的核函数,它们(包括我们常使用的高斯kernel)需要满足一个定理(默塞尔定理),这是因为SVM有很多数值优化技巧,为了有效地求解参数Θ,需要相似度函数满足默塞尔定理,这样才能确保SVM包能够使用优化的方法来求解参数Θ。
一些其它可能会被用到的kernels(很少使用): 多项式核函数,将x与l(landmark)的内积做为一种相似度的度量,如上图所示,它的一般形式为(xTl+constant)degree,有两个参数,一个是constant,一个是degree。多项式核函数一般会要求x与l都是非负的,这样它们的内积才是正的
一些更少用到的核函数:字符串核函数-如果你输入的数据为字符串的话,有时会用到这个核函数,来比较两个对象之间的相似度。卡方核函数,直方图交叉核函数。
我们基本上很少用到这些核函数(用得最多的是高斯kernel与linear kernel),但是碰到它们时,要知道它们为核函数的定义.
SVM中的多分类问题
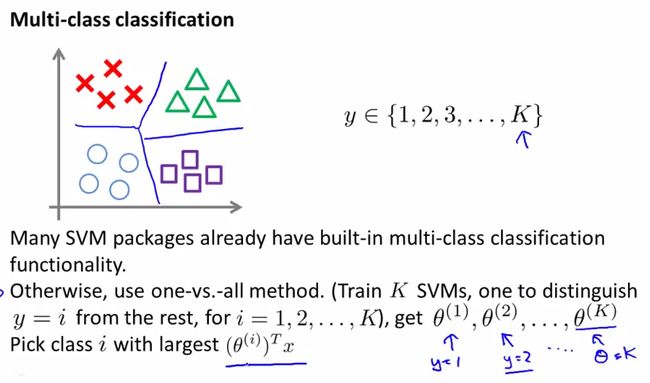
当我们遇到多分类的问题时,如何有效地画出多分类的边界呢?
大多数的SVM都已经内置了多分类问题的软件包,我们可以直接使用。
另一种方法时使用one-vs.-all方法(参考之前的),训练K个SVM(如果有K个分类的话),这样得出K个参数θ向量(每一个参数θ都是将这一类与其它类分别时所求的θ),然后预测时选择最大时的θTx所表示的那个class
logistic regression/SVM/神经网络比较
我们将logistic regression的cost function进行了修改得出了SVM,那么我们在什么情况下应该使用什么算法呢?
如果我们的features要比样本数要大的话(如n=10000,m=10-1000),我们使用logistic regression或者linear kernel,因为在样本较少的情况下,我们使用线性分类效果已经很好了,我们没有足够多的样本来支持我们进行复杂的分类。
如果n较小,m大小适中的话,使用SVM with Gaussion kernel.如我们之前讲的有一个二维(n=2)的数据集,我们可以使用高斯核函数很好的将正负区分出来.
如果n较小,m非常大的话,会创建一些features,然后再使用logistic regeression 或者linear kernel。因为当m非常大的话,使用高斯核函数会较慢
logistic regeression 与linear kernel是非常相似的算法,如果其中一个适合运行的话,那么另一个也很有可能适合运行。
我们使用高斯kernel的范围很大,当m多达50000,n在1-1000(很常见的范围),都可以使用SVM with 高斯kernel,可以解决很多logistic regression不能解决的问题。
神经网络在任何情况下都适用,但是有一个缺点是它训练起来比较慢,相对于SVM来说
SVM求的不是局部最优解,而是全局最优解
相对于使用哪种算法来说,我们更重要的是掌握更多的数据,如何调试算法(bias/variance),如何设计新的特征变量,这些都比是使用SVM还是logistic regression重要。
但是SVM是一种被广泛使用的算法,并且在某个范围内,它的效率非常高,是一种有效地学习复杂的非线性问题的学习算法。
logistic regression,神经网络,SVM这三个学习算法使得我们可以解决很多前沿的机器学习问题。