自我复制、风行机械兽与生命游戏:下一个伟大的事情会是非常小的
本报道整理自CA Technologies API学院API架构主管Mike Amundsen在2014年ArchSummit大会北京站的主题演讲分享:《冯诺依曼等技术先贤留下的API规模经济启示》。
本次分享将围绕三件事情:自我复制、风行机械兽(Strandbeest)和Conway的生命游戏。从这三件事情当中,我们回顾过去的50年,并展望商业、软件和API生态的未来。
我们现在正处于一个十字路口。在过去的十几年间,我们的软件世界遇到了很多问题,其中最大的一个问题就是:整个软件世界在激烈的增长,消费力远超从前,但软件的实践却缺乏足够的可扩展性。这是什么意思?想想移动设备。有人预测说2015年全球连线设备的总数会超过150亿,还有人预测说2020年这个数字会超过400亿。
这意味着什么?大家觉得我们现在从编写软件、debug、测试到部署的这套流程实践的如何?我们以怎样的频率来做这件事?持续集成的理念建议我们每天都要把这套流程跑很多次,但我们实际上一周有做到一次吗?再想想网络,我们今天这个数量级的设备,大家觉得网络的速度如何?如果我们再添加100亿台设备,你觉得网络延时是会变好还是变差?
今天的软件世界太拥挤。我们构建软件的方式太拥挤。一大堆人涌进来想要做很多很多事情,但这很多事情所需要的代码量、工作量,根本不是我们能负担得起的。越是更多人进来插一脚,越是交通拥堵,结果所有人都卡在路上无法前进了。
我们需要新的思路来解决我们想要解决的那些问题。一些创新的想法。而前进的方向,其实历史早已为我们指明。
回顾历史
25年前,刚刚过30岁的Tim Berners-Lee完成了万维网(WWW)雏形的构思。他说,现在我们有了internet,有了TCP/IP协议,有了DNS体系,只要把这三个东西搅拌到一起,这就是可以连接全球的万维网啦。这个体系的设计中没有层级,节点和节点之间通过随机的方式连接,这种设计让万维网可以以很小的成本扩展到无限大(从软件的角度而言)。
几乎在同一个时间段,英国数学家John H. Conway完成了一本大块头著作:ATLAS of Finite Groups,这部关于数论的巨作详细分析了复数的各种特性。这实际上是Conway的第六本书,此前的每一本新作都在数论方面达到了一个新的高度;但更有意思的是Conway在1970年发布在Scientific American上的一篇文章,描述他从一个自创的格子游戏中发现的“新生命”。
二十年后,一位叫做Theo Jansen的荷兰艺术家发明了一个叫做Strandbeest的机械。这个风行机械兽令人着迷的一点在于它的设计方式:它不是由人设计的,而是由电脑设计的。
Tim Berners-Lee,John Conway,Theo Jansen。这三个人没有见过面,但却紧密的联系在一起。
连接他们的那个人叫做冯诺依曼(John von Neumann)。
冯诺依曼在1903年的冬天出生在匈牙利的一个贵族家庭,出生时他的名字叫做Neumann Janos。小诺依曼6岁就能够做两个八位数的除法,8岁就能理解微积分,19岁就发表了两篇数学论文,22岁拿到数学博士,同时还选修了化学和实验物理。他总是能量充沛,繁忙而充分享受生活。
毕业后他在匈牙利本地教书,没几年就受邀去了美国普林斯顿,移民的时候改名为John von Neumann。那是1930年代,普林斯顿的黄金时代,他在那里认识了图灵、爱德华·泰勒、爱因斯坦、哥德尔、狄拉克、奥本海默、以及现代互联网之父Venneavar Bush。诺依曼在普林斯顿的生活是多产的,不过今天我重点只关心两个部分:
- 他对于计算机架构的描述工作
- 他提出的细胞自动机(cellular automata)概念
这两个方向的研究直接影响了我们今天的API经济如何扩展的问题。
诺依曼跟图灵的接触是在1930年代末期,他在那个时候了解了通用图灵机的理论,该理论的关键在于让图灵机能够从同一个“存储介质”上读取有关问题的描述和跟问题相关的数据——图灵用无限长度的纸条来形容这个存储介质。那时候的“程序”就是在一个大板子上把一堆开关扳来扳去,一个地方错了都要重来。
十年后,诺依曼在EDVAC项目工作,期间写了一篇论文描述一种计算机架构,可以把数据和程序一起存储在存储器中的同一个地址空间下。后来他去ENIAC项目工作,其中最原始的编程指令集就是他写的,之后才有Grace Hopper在ENIAC上设计COBOL语言和编译器。
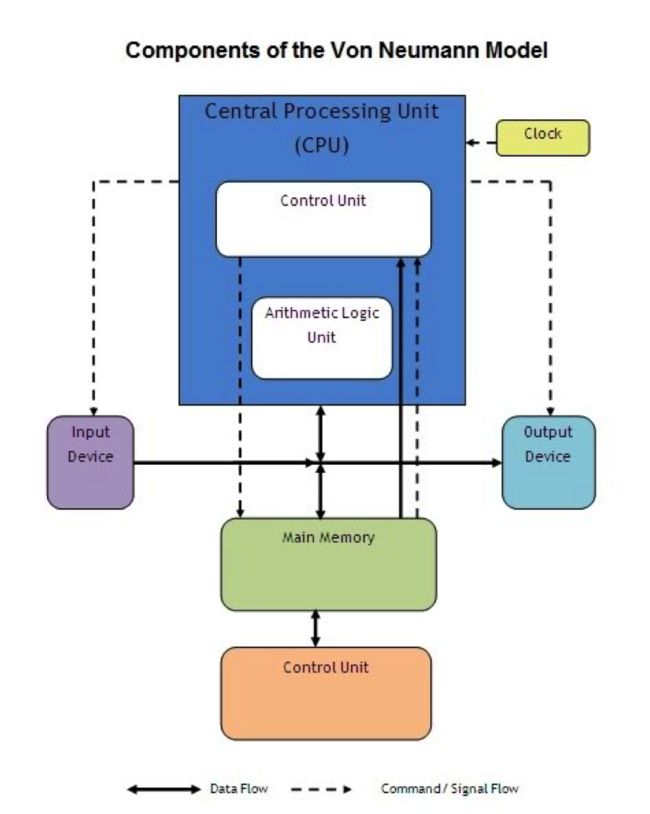
这种架构在今天被称为冯诺依曼结构,内存和计算单元在一起,还有一个时钟。今天的大型主机、台式机、平板、手机都延续了这种架构。
但其实呢,这个架构是他的第二版设计。对于“计算机架构应该如何设计”这件事,诺依曼还提供了另一个构想,是他在曼哈顿项目期间跟乌拉姆(Stanislav Ullam)一起讨论出来的。这一版构想并没有用在项目中,而是在诺依曼去世之后发布为一本小书。书的名字叫做Theory of Self Reproducing Automata——自复制自动机理论。
这个架构没有中央计算单元,没有时钟,也没有线性编程模型。有的仅仅是一堆格子和可以自我复制的小点点(也就是细胞自动机)。
面向自动机的编程方式和我们所知的面向冯诺依曼结构机器的编程方式完全不同。事实上我们不对自动机编程。我们仅仅是给它们设定规则。细胞自动机们接受了这些规则后会从此自己行动,不需要我们再给它们下什么指令,而结果则出人意料的“涌现”出来。
之后的数十年间,无数学者被细胞自动机的理论所吸引而做了大量研究,也有很多成果,比如Stephen Wolfram的著作A New Kind of Science和以此为基础制作的搜索引擎Web服务Wolfram Alpha,比如蜂群/蚁群理论,比如Bubble Growth Theory等等。不过其中最引人注目的成果,还当属Conway的生命游戏。
John H. Conway在1937年冬天出生于英国,当时诺依曼还在普林斯顿授课。小康威在二战的阴影中长大成人,在剑桥大学拿到了自己的数学本科和博士。期间他迷上了Backgammon这个游戏,跟自己见到的所有人挑战这个游戏。Conway一生致力于数论的研究,而他对游戏的热爱导致了组合游戏理论(Combinatorial Game Theory,简称CGT)的诞生。他在数论方面写了一系列的书,包括On Numbers and Games和Winning Ways for your Mathematical Plays,不过最有意思的是他在1970年发布在《科学美国人》杂志(Scientific American)上的那篇Conway's Game of Life。
游戏世界就是诺依曼自动机架构中的一堆格子,每个“自动机”都有八个格子与其相邻。游戏规则仅有三条:
- 生存规则:8个邻格中有2-3个“邻居”的自动机可以存活到下一回合
- 死亡规则:8个邻格中有4个或以上“邻居”的自动机在下一回合死于人口过载;1个或以下“邻居”的自动机在下一回合死于孤独
- 出生规则:8个邻格中有3个“邻居”的空格子在下一回合生出一个新的自动机
Conway搞到了一台PDP-7计算机来运行这套游戏,结果发现了一些奇特的“生命”。无论初始环境怎样不同,最终都会发现这些“生命”的出现。有一类是在本地的两个状态间循环摆动的(oscillators),有一类是在本地静止的(still lifes),但是最神奇的是一种叫做滑翔机的“生命”(spaceships),这个小东西会沿着格子往一个方向不断爬行。
启动一次新的初始环境的时候,没有人会知道结果是怎样的。这跟我们传统以来一直抱有的思路是不同的。以前的我们总是先构想一个目标,一个想要达成的结果,然后找到某种方式到达那种状态。
而现在,我们需要学会在不知道结果的情况下开始我们的旅程。我们不再“创造”结果,我们要学会“发现”结果。这结果在一开始是完全未知的,是在旅途过程中突然涌现的。
我们今天的软件世界还没太适应这种做法,不过已经有一位前辈走在了这条道路上,那就是荷兰人Theo Jansen。Conway在普林斯顿期间,这位40多岁的艺术家刚刚做完了一个画画机器,读完了Richard Dawkins的The Blind Watchmaker一书,决定尝试做一个新玩意儿:建造一种便宜的机械,能够在海边的沙滩上自己建造沙丘以抵抗海平面升高对城市的威胁(众所周知荷兰这个国家是最怕海平面升高的)。
这个名为Strandbeest的机械的设计制作过程有很多精妙之处,不过最有趣的是机械腿的设计过程。轮子式的机械腿无法在沙滩上活动,Theo的机械需要一种既能够在潮湿坚硬的沙地上又能够在干燥松软的沙滩上行动的腿,这个腿该如何设计呢?Theo设计了一种11根“骨骼”组成的结构,然后把寻找最佳比例的工作丢给了电脑上的自动机们。自动机们以1500种随机初始比例为起点,然后按照Theo设计的规则生长、进化,从中挑出最好的100个;这100条腿的骨骼再被打乱随机重组成1500条腿,继续生长进化,再选出100个活的最好的,再生成1500个新的腿,如此这般。过了几个月后,自动机们进化出了一条“最好的腿”,11根骨骼的比例让机械兽在沙滩上行走自如。
这个设计腿的思路后来又用于给机械兽添加新的“生存能力”,包括遇到海浪自动撤退、储存风能备用、寻找更合适的地点等。这整个过程被记录在Theo写的The Great Pretender一书当中,这本书很好,即使你对机械不感兴趣我也推荐你看看。
展望未来
这三个故事展示了计算机能够做什么(而不单纯是我们能让机器做什么)。2001太空漫游里面有一个叫做黑色碑石(monolith)的东西,这是一种能够自己探索太空的自动机。冯诺依曼研究生涯的最后阶段就是在构思这样一种自动机,能够自己探索、自己在陌生的星球着陆、在星球本地收集素材复制自己,然后复制出来的一堆自动机又能够继续往宇宙更深处扩散,从而探索更大的宇宙。这种可以自我复制的宇宙飞船的另一个名字叫做von Neumann Probe,正是黑色碑石的原型。
现在想想那150亿的设备。或者400亿的设备。它们也是一样的。我们实在做不到一一告诉它们要做这个或者要做那个——无论是心力还是创意都不够。我们应该把事情简化起来,给他们设定规则,让它们去自己探索浩瀚的Web宇宙。
梅拉妮·米歇尔的《复杂》一书(Complexity: A Guided Tour)当中描述了一个捡罐子机器人的设计(演化)过程。软件在一开始随机生成了100个机器人,让它们在格子里捡罐子,然后把表现最佳的两个机器人做一个“交配”,依据它们俩的痕迹再随机拼出100个新的机器人。如此反复,机器人捡罐子走的路径就越来越短,效率越来越高。
相比之下,无论是Google还是IBM的学习模型都过于倾向(大)数据分析。这种学习方式也有很大的成果,但它有很大的局限性。Google的Peter Norvig曾经表示这种数据分析方式开始遇到瓶颈了:
“我们的数据是更多了,而我们的系统变好了多少呢?它当然是仍在进步的,但我们从中获得的好处远不如从前。”
这个发现并不令人惊讶。事实上回顾互联网发展的历程,最早的Yahoo索引是以人为排序为基础的等级序列,把人认为有价值的内容放在前面。而Google则不这样做,它发现人认为什么内容有价值并不是最重要的,最重要的是页面之间的链接:当越来越多的互联网用户将页面相连,这个价值就涌现出来了。这一现象跟万维网本身一样,是一个具有无限扩展性的网络。
我们一直在忽略自动机的力量。现在是时候做出改变了。
下一个伟大的事情会是非常小的。不,我说的不是微服务,也不是可穿戴设备,也不是纳米机器人。
我说的“小”是指用“很少的代码”写软件,甚至于“不用代码”写软件!
Leonard Richardson说过一句话:“迷宫”一词是类超链应用的一个比喻。这个意思并不仅是说由超链接组成的Web就像迷宫一样,同时还有另一个意思,那就是一切迷宫只要用最基本的规则就都能走出来。面对对于任何一个二维迷宫,我们所需要的全部规则都在这儿了:
m.rules = {
'east': ['south', 'east', 'north', 'west'],
'south': ['west', 'south', 'east', 'north'],
'west': ['north', 'west', 'south', 'east'],
'north': ['east', 'north', 'west', 'south']
};
我们虽然不知道迷宫的出口长啥样,但我们难道要因此而驻足不前吗?我们在现在这个地方原地打转了太久了,我已经等得不耐烦啦。
千里之行,始于足下。让我们开启新的旅程吧!