【题解】 2015 ACM/ICPC Asia Regional Changchun Online (5+2)

第一次网络赛 怎么说 出题数还可以 可惜没靠自己打入(巨巨学长们一举冲入前百

最后那俩没能出的一个后缀树组/字符串最小表示法+KMP 另一个lucas定理+中国剩余定理。。。(只是赛后了解到了 以后要把这几个算法补上

其他题用的都是简单算法和数据结构 不过还是卡了两处

【1001】 Alisha's Party(优先队列模拟)

Alisha’s Party

Time Limit: 3000/2000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 1066    Accepted Submission(s): 294

Problem Description

Princess Alisha invites her friends to come to her birthday party. Each of her friends will bring a gift of some value  v , and all of them will come at a different time. Because the lobby is not large enough, Alisha can only let a few people in at a time. She decides to let the person whose gift has the highest value enter first.

Each time when Alisha opens the door, she can decide to let  p  people enter her castle. If there are less than  p  people in the lobby, then all of them would enter. And after all of her friends has arrived, Alisha will open the door again and this time every friend who has not entered yet would enter.

If there are two friends who bring gifts of the same value, then the one who comes first should enter first. Given a query  n  Please tell Alisha who the  n−th  person to enter her castle is.

 

Input

The first line of the input gives the number of test cases,  T  , where  1≤T≤15 .

In each test case, the first line contains three numbers  k,m  and  q  separated by blanks.  k  is the number of her friends invited where  1≤k≤150,000 . The door would open m times before all Alisha’s friends arrive where  0≤m≤k . Alisha will have  q  queries where  1≤q≤100 .

The  i−th  of the following  k  lines gives a string  Bi , which consists of no more than  200  English characters, and an integer  vi ,  1≤vi≤108 , separated by a blank.  Bi  is the name of the  i−th  person coming to Alisha’s party and Bi brings a gift of value  vi .

Each of the following  m  lines contains two integers  t(1≤t≤k)  and  p(0≤p≤k)  separated by a blank. The door will open right after the  t−th  person arrives, and Alisha will let  p  friends enter her castle.

The last line of each test case will contain  q  numbers  n1,...,nq  separated by a space, which means Alisha wants to know who are the  n1−th,...,nq−th  friends to enter her castle.

Note: there will be at most two test cases containing  n>10000 .

 

Output

For each test case, output the corresponding name of Alisha’s query, separated by a space.

 

Sample Input

   
   
   
   

    
    
    
    1
5 2 3
Sorey 3
Rose 3
Maltran  3
Lailah 5
Mikleo  6
1 1
4 2
1 2 3
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    Sorey Lailah Rose
   
   
   
   

 

Source

2015 ACM/ICPC Asia Regional Changchun Online

 

Recommend

hujie   |   We have carefully selected several similar problems for you:   5449  5448  5447  5446  5445 

 

优先队列模拟 阿丽莎过生日 邀请了k个朋友去做客 但是她卧室太小了 所以先让他们到客厅 每个朋友都带着价值v的礼物来的 阿丽莎会开卧室门m次 当第t个人来了后 她会带p个人进卧室把礼物放下 礼物价值大的先进 相同价值的 先来的先进 最后一次开门后如果还有没放下礼物的按照同样规定进卧室放礼物

没理解好 当时在纠结按m顺序来开门还是按t来开 后来WA了发 排了下序T了发。。。又改回去改了改WA。。。改回来 T。。。然后又T。。。然后不敢交了

最后楠神想起上次就是被杭电服务器给坑了 再交次吧。。。果然……2000ms变成1679@#￥#@# 糊弄鬼啊。。同样代码……哎 早起该洗脸

正确做法就是按t排个序 然后优先队列模拟开门放礼物 最后按询问输出第a次进入的人的名字即可

代码如下:

#include <bits/stdc++.h>

using namespace std;

typedef struct Friend
{
    char name[233];
    int v,id;
    bool operator <(const struct Friend a)const//优先队列排序 逆序排 越小越靠后
    {
        return v == a.v? id > a.id: v < a.v;//礼物价值相同的 id大的靠后 不同的 价值小的靠后
    }
}Friend;

typedef struct Enter
{
    int t,p;
    bool operator < (const struct Enter a)const//按t排序开门
    {
        return t == a.t? p > a.p: t < a.t;
    }
}Enter;

Enter en[155555];//开门
Friend f[155555];//朋友姓名和礼物价值
Friend to[155555];//第i次进卧室的朋友
int ques[111];//询问

int main()
{
    int t,k,m,q,i,j,mx,cnt,sum;

    scanf("%d",&t);
    while(t--)
    {
        priority_queue <Friend> qq;
        scanf("%d %d %d",&k,&m,&q);
        for(i = 0; i < k; ++i)
        {
            scanf("%s %d",f[i].name,&f[i].v);
            f[i].id = i;
        }

        for(i = 0; i < m; ++i) scanf("%d %d",&en[i].t,&en[i].p);
        en[m].t = k;//最后还有未进的按规则进入 所以加一次开门
        en[m].p = k;
        sort(en,en+m+1);

        mx = 0;
        for(i = 0; i < q; ++i)
        {
            scanf("%d",&ques[i]);
            mx = max(mx,ques[i]);//找出最大询问 缩短时间
        }

        cnt = 0;
        sum = 1;

        for(i = 0; i <= m && sum <= mx; ++i)
        {
            while(cnt < en[i].t)//未达到开门需要人数 朋友入队(进客厅
            {
                qq.push(f[cnt++]);
            }

            while(!qq.empty() && en[i].p-- && sum <= mx)//p个人进卧室 队列空了/足够询问 停止进入
            {
                to[sum++] = qq.top();
                qq.pop();
            }
        }

        for(i = 0; i < q; ++i)
        {
            if(i) putchar(' ');
            printf("%s",to[ques[i]].name);
        }
        puts("");
    }

    return 0;
}

【1002】 Ponds(拓扑+BFS)

Ponds

Time Limit: 1500/1000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 754    Accepted Submission(s): 250

Problem Description

Betty owns a lot of ponds, some of them are connected with other ponds by pipes, and there will not be more than one pipe between two ponds. Each pond has a value  v .

Now Betty wants to remove some ponds because she does not have enough money. But each time when she removes a pond, she can only remove the ponds which are connected with less than two ponds, or the pond will explode.

Note that Betty should keep removing ponds until no more ponds can be removed. After that, please help her calculate the sum of the value for each connected component consisting of a odd number of ponds

 

Input

The first line of input will contain a number  T(1≤T≤30)  which is the number of test cases.

For each test case, the first line contains two number separated by a blank. One is the number  p(1≤p≤104)  which represents the number of ponds she owns, and the other is the number  m(1≤m≤105)  which represents the number of pipes.

The next line contains  p  numbers  v1,...,vp , where  vi(1≤vi≤108)  indicating the value of pond  i .

Each of the last  m  lines contain two numbers  a  and  b , which indicates that pond  a  and pond  b  are connected by a pipe.

 

Output

For each test case, output the sum of the value of all connected components consisting of odd number of ponds after removing all the ponds connected with less than two pipes.

 

Sample Input

   
   
   
   

    
    
    
    1
7 7
1 2 3 4 5 6 7
1 4
1 5
4 5
2 3
2 6
3 6
2 7
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    21
   
   
   
   

 

Source

2015 ACM/ICPC Asia Regional Changchun Online

 

Recommend

hujie   |   We have carefully selected several similar problems for you:   5449  5448  5447  5446  5445 

 

有环无向图 保证输入无重边 每个点具有价值 要求把所有度为0或1的点及其所连边去掉 变成一个个子图 求点为奇数的子图们的总价值(点值和)

拓扑去点 然后按要求找出去点后符合条件的图 把价值加起来即可 注意总价值会超int

代码如下:

#include <bits/stdc++.h>
#define ll long long

using namespace std;

typedef struct Edge
{
    int v,next;
}Edge;

Edge eg[233333];//邻接表
int head[10010],val[10010],in[10010],tp,n;//head表头 val点值 in点度
bool vis[10010];//访问标记

void Add(int u,int v)//加点
{
    eg[tp].v = v;
    eg[tp].next = head[u];
    head[u] = tp++;
}

void Topo()//拓扑去度<=1的点
{
    int i,u,v;
    queue <int> q;
    for(i = 1; i <= n; ++i)//先把度<=1的点入队并标记
    {
        if(in[i] <= 1)
        {
            q.push(i);
            vis[i] = 1;
        }
    }

    while(!q.empty())
    {
        u = q.front();
        q.pop();
        for(i = head[u]; i != -1; i = eg[i].next)//遍历减度入队
        {
            v = eg[i].v;
            if(vis[v]) continue;
            in[v]--;
            if(in[v] <= 1)
            {
                q.push(v);
                vis[v] = 1;
            }
        }
    }

}

ll Search(int u)//遍历u所在子图 返回该图价值
{
    int v,i,cnt = 1;//初始点数1(u)
    ll ans = val[u];//初始价值u点价值
    queue <int> q;
    q.push(u);
    vis[u] = 1;
    while(!q.empty())
    {
        u = q.front();
        q.pop();
        for(i = head[u]; i != -1; i = eg[i].next)
        {
            v = eg[i].v;
            if(vis[v]) continue;
            cnt++;
            q.push(v);
            ans += val[v];
            vis[v] = 1;
        }
    }
    if(cnt%2) return ans;//奇数点价值为点值和 偶数点价值0
    else return 0;
}

int main()
{
    int t,m,i,u,v;
    ll sum;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d %d",&n,&m);
        memset(head,-1,sizeof(head));
        memset(vis,0,sizeof(vis));
        memset(in,0,sizeof(in));
        sum = tp = 0;

        for(i = 1; i <= n; ++i)
            scanf("%d",&val[i]);

        for(i = 0; i < m; ++i)
        {
            scanf("%d %d",&u,&v);
            Add(u,v);
            Add(v,u);
            in[u]++;
            in[v]++;
        }

        Topo();
        for(i = 1; i <= n; ++i)
        {
            if(vis[i]) continue;
            sum += Search(i);
        }
        printf("%I64d\n",sum);
    }
    return 0;
}

【1005】 Travel(并查集)

Travel

Time Limit: 1500/1000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 495    Accepted Submission(s): 205

Problem Description

Jack likes to travel around the world, but he doesn’t like to wait. Now, he is traveling in the Undirected Kingdom. There are  n  cities and  m  bidirectional roads connecting the cities. Jack hates waiting too long on the bus, but he can rest at every city. Jack can only stand staying on the bus for a limited time and will go berserk after that. Assuming you know the time it takes to go from one city to another and that the time Jack can stand staying on a bus is  x  minutes, how many pairs of city  (a,b)  are there that Jack can travel from city  a  to  b  without going berserk?

 

Input

The first line contains one integer  T,T≤5 , which represents the number of test case.

For each test case, the first line consists of three integers  n,m  and  q  where  n≤20000,m≤100000,q≤5000 . The Undirected Kingdom has  n  cities and  m bidirectional roads, and there are  q  queries.

Each of the following  m  lines consists of three integers  a,b  and  d  where  a,b∈{1,...,n}  and  d≤100000 . It takes Jack  d  minutes to travel from city  a  to city  b and vice versa.

Then  q  lines follow. Each of them is a query consisting of an integer  x  where  x  is the time limit before Jack goes berserk.

 

Output

You should print  q  lines for each test case. Each of them contains one integer as the number of pair of cities  (a,b)  which Jack may travel from  a  to  b  within the time limit  x .

Note that  (a,b)  and  (b,a)  are counted as different pairs and  a  and  b  must be different cities.

 

Sample Input

   
   
   
   

    
    
    
    1
5 5 3
2 3 6334
1 5 15724
3 5 5705
4 3 12382
1 3 21726
6000
10000
13000
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    2
6
12
   
   
   
   

 

Source

2015 ACM/ICPC Asia Regional Changchun Online

 

Recommend

hujie   |   We have carefully selected several similar problems for you:   5449  5448  5447  5446  5445 

 

n个城市 m个旅游方案 q次查询

每个方案u v w表示在u跟v间旅游需要w时间

旅游多对城市花费时间为这些花费中的最大值 每次询问花x时间能观赏多少对城市

每个城市可以当做图中一个点 两点间花费可看做一条带权无向边 以wi时间游览ui vi 可同时游览u,v间时间花费不大于wi的城市

也就是说 需要不大于wi时间的与u成对的城市 和与v成对的城市 可互相访问

演化成两个集合间城市两两访问 把输入按w排序 然后走并查集就行 同时开个数组 记录与每个点可访问的点数(即该点所在集合包含的点数)

每加一条边时 新加入的可访问城市对数即为两集合点数相乘再乘2(无向边)

代码如下:

#include <bits/stdc++.h>

using namespace std;

typedef struct Edge
{
    int u,v,w;
    bool operator < (const struct Edge a)const
    {
        return w < a.w;
    }
}Edge;

Edge eg[100100];//邻接表存图
int ned[100100];//不超过x时间能访问的城市对
int pre[100100];//并查集
int can[100100];//集合中点数

int Find(int x)
{
    return x == pre[x]? pre[x]: (pre[x] = Find(pre[x]));
}

int main()
{
    int t,n,m,q,i,k,r,ans,x;
    scanf("%d",&t);

    while(t--)
    {
        scanf("%d %d %d",&n,&m,&q);
        memset(ned,0,sizeof(ned));

        for(i = 1; i <= n; ++i)
        {
            pre[i] = i;
            can[i] = 1;
        }

        for(i = 0; i < m; ++i)
            scanf("%d %d %d",&eg[i].u,&eg[i].v,&eg[i].w);

        sort(eg,eg+m);
        for(i = 0; i < m; ++i)
        {
            k = Find(eg[i].v);
            r = Find(eg[i].u);
            if(k == r) continue;//两个点在一个集合 没有新城市对产生
            if(k > r) pre[k] = r;//始终以小节点为集合祖先
            else pre[r] = k;
            ned[eg[i].w] += can[r]*can[k]*2;//以w时间能访问的城市对
            can[k] = can[r] += can[k];//两集合合并后生成新集合为两集合点数和
        }

        ans = 0;
        for(i = 1; i <= 100000; ++i)//更新数组为不超过i时间能访问的最多城市对
        {
            ans += ned[i];
            ned[i] = ans;
        }

        while(q--)
        {
            scanf("%d",&x);
            printf("%d\n",ned[x]);
        }
    }

    return 0;
}

【1007】 The Water Problem(RMQ/线段树)

The Water Problem

Time Limit: 1500/1000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 337    Accepted Submission(s): 275

Problem Description

In Land waterless, water is a very limited resource. People always fight for the biggest source of water. Given a sequence of water sources with  a1,a2,a3,...,an representing the size of the water source. Given a set of queries each containing  2  integers  l  and  r , please find out the biggest water source between  al  and  ar .

 

Input

First you are given an integer  T(T≤10)  indicating the number of test cases. For each test case, there is a number  n(0≤n≤1000)  on a line representing the number of water sources.  n  integers follow, respectively  a1,a2,a3,...,an , and each integer is in  {1,...,106} . On the next line, there is a number  q(0≤q≤1000)  representing the number of queries. After that, there will be  q  lines with two integers  l  and  r(1≤l≤r≤n)  indicating the range of which you should find out the biggest water source.

 

Output

For each query, output an integer representing the size of the biggest water source.

 

Sample Input

   
   
   
   

    
    
    
    3
1
100
1
1 1
5
1 2 3 4 5
5
1 2
1 3
2 4
3 4
3 5
3
1 999999 1
4
1 1
1 2
2 3
3 3
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    100
2
3
4
4
5
1
999999
999999
1
   
   
   
   

 

Source

2015 ACM/ICPC Asia Regional Changchun Online

 

Recommend

hujie   |   We have carefully selected several similar problems for you:   5449  5448  5447  5446  5445 

 

RMQ模板 当时脑残了 RMQ写搓了 紧张之下猛敲线段树TOT 对不起队友……(楠神还特意提醒 用线段树吧)

回来用RMQ重敲了遍 一发过 还是不熟练啊 要不比赛时就不会卡壳了……

代码如下:

#include <bits/stdc++.h>

using namespace std;

int rmq[1111][10];

int main()
{
    int t,n,q,i,j,k,l,r;
    scanf("%d",&t);

    while(t--)
    {
        scanf("%d",&n);
        for(i = 1; i <= n; ++i) scanf("%d",&rmq[i][0]);

        for(j = 1; 1<<j <= n; ++j)
            for(i = 1; i+(1<<j)-1 <= n; ++i)
                rmq[i][j] = max(rmq[i][j-1],rmq[i+(1<<(j-1))][j-1]);

        scanf("%d",&q);
        while(q--)
        {
            scanf("%d %d",&l,&r);
            k = log10(r-l+1)/log10(2);
            printf("%d\n",max(rmq[l][k],rmq[r-(1<<k)+1][k]));
        }
    }

    return 0;
}

【1008】 Elven Postman(暴力建排序树+树上找点)

Elven Postman

Time Limit: 1500/1000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 352    Accepted Submission(s): 187

Problem Description

Elves are very peculiar creatures. As we all know, they can live for a very long time and their magical prowess are not something to be taken lightly. Also, they live on trees. However, there is something about them you may not know. Although delivering stuffs through magical teleportation is extremely convenient (much like emails). They still sometimes prefer other more “traditional” methods.

So, as a elven postman, it is crucial to understand how to deliver the mail to the correct room of the tree. The elven tree always branches into no more than two paths upon intersection, either in the east direction or the west. It coincidentally looks awfully like a binary tree we human computer scientist know. Not only that, when numbering the rooms, they always number the room number from the east-most position to the west. For rooms in the east are usually more preferable and more expensive due to they having the privilege to see the sunrise, which matters a lot in elven culture.

Anyways, the elves usually wrote down all the rooms in a sequence at the root of the tree so that the postman may know how to deliver the mail. The sequence is written as follows, it will go straight to visit the east-most room and write down every room it encountered along the way. After the first room is reached, it will then go to the next unvisited east-most room, writing down every unvisited room on the way as well until all rooms are visited.

Your task is to determine how to reach a certain room given the sequence written on the root.

For instance, the sequence 2, 1, 4, 3 would be written on the root of the following tree.

 

Input

First you are given an integer  T(T≤10)  indicating the number of test cases.

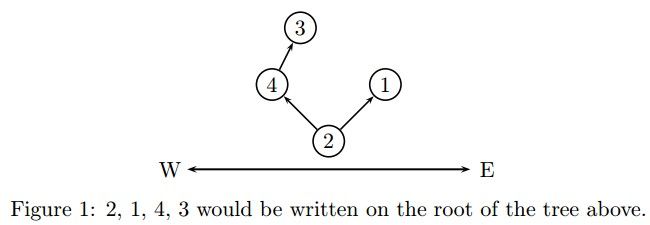
For each test case, there is a number  n(n≤1000)  on a line representing the number of rooms in this tree.  n  integers representing the sequence written at the root follow, respectively  a1,...,an  where  a1,...,an∈{1,...,n} .

On the next line, there is a number  q  representing the number of mails to be sent. After that, there will be  q  integers  x1,...,xq  indicating the destination room number of each mail.

 

Output

For each query, output a sequence of move ( E  or  W ) the postman needs to make to deliver the mail. For that  E  means that the postman should move up the eastern branch and  W  the western one. If the destination is on the root, just output a blank line would suffice.

Note that for simplicity, we assume the postman always starts from the root regardless of the room he had just visited.

 

Sample Input

   
   
   
   

    
    
    
    2
4
2 1 4 3
3
1 2 3
6
6 5 4 3 2 1
1
1
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    E

WE
EEEEE
   
   
   
   

 

Source

2015 ACM/ICPC Asia Regional Changchun Online

 

Recommend

hujie   |   We have carefully selected several similar problems for you:   5449  5448  5447  5446  5445 

 

当时看了半天看出来是排序树直接愣了 弱渣不会啊TOT 不过后来仔细读了读 因为给的建树是遍历建树 而且节点也不多 暴力建一颗就行 刚开始考虑空间复杂度脑残了 当做满二叉考虑了 RE好几发 后来无脑又交了几发RE(也是最后了 做的头胀 随意交了。。。(反正罚时已经这样了 而且另俩题看着也不太友好。。。)) 最后发现改成指针过了
 

代码如下:

#include <bits/stdc++.h>

using namespace std;

typedef struct Node Node;
typedef struct Node* Nd;

struct Node
{
    Nd lchild,rchild;
    int data;
};

void Add(Nd tr,int x)
{
    Nd q = (Nd)malloc(sizeof(Node));
    Nd t = tr;
    q->data = x;
    q->lchild = q->rchild = NULL;

    while(1)
    {
        if(x > t->data)//x大于当前节点 往右子树加
        {
            if(!t->rchild)//访问到叶子 加到右孩子
            {
                t->rchild = q;
                return;
            }
            t = t->rchild;
        }
        else//否则 往左子树加
        {
            if(!t->lchild)//访问到叶子 加到左孩子
            {
                t->lchild = q;
                return;
            }
            t = t->lchild;
        }
    }
}

void Search(Nd tr,int x)
{
    Nd t = tr;
    while(t->data != x)
    {
        if(x > t->data)
        {
            putchar('W');
            t = t->rchild;
        }
        else
        {
            putchar('E');
            t = t->lchild;
        }
    }
}

int main()
{
    int t,n,i,x,q;

    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        Nd tr = (Nd)malloc(sizeof(Node));
        scanf("%d",&tr->data);
        tr->lchild = tr->rchild = NULL;//初始化根节点

        for(i = 1; i < n; ++i)
        {
            scanf("%d",&x);
            Add(tr,x);//加点
        }

        scanf("%d",&q);
        while(q--)
        {
            scanf("%d",&x);
            Search(tr,x);//查x
            puts("");
        }
    }

    return 0;
}

【1006】 Favorite Donut (KMP+最小表示法)

Favorite Donut

Time Limit: 1500/1000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 2015    Accepted Submission(s): 489

Problem Description

Lulu has a sweet tooth. Her favorite food is ring donut. Everyday she buys a ring donut from the same bakery. A ring donut is consists of  n  parts. Every part has its own sugariness that can be expressed by a letter from  a  to  z  (from low to high), and a ring donut can be expressed by a string whose i-th character represents the sugariness of the  i−th  part in clockwise order. Note that  z  is the sweetest, and two parts are equally sweet if they have the same sugariness.

Once Lulu eats a part of the donut, she must continue to eat its uneaten adjacent part until all parts are eaten. Therefore, she has to eat either clockwise or counter-clockwise after her first bite, and there are  2n  ways to eat the ring donut of  n  parts. For example, Lulu has  6  ways to eat a ring donut  abc :  abc,bca,cab,acb,bac,cba . Lulu likes eating the sweetest part first, so she actually prefer the way of the greatest lexicographic order. If there are two or more lexicographic maxima, then she will prefer the way whose starting part has the minimum index in clockwise order. If two ways start at the same part, then she will prefer eating the donut in clockwise order. Please compute the way to eat the donut she likes most.

 

Input

First line contain one integer  T,T≤20 , which means the number of test case.

For each test case, the first line contains one integer  n,n≤20000 , which represents how many parts the ring donut has. The next line contains a string consisted of  n  lowercase alphabets representing the ring donut.

 

Output

You should print one line for each test case, consisted of two integers, which represents the starting point (from  1  to  n ) and the direction ( 0  for clockwise and  1  for counterclockwise).

 

Sample Input

   
   
   
   

    
    
    
    2
4
abab
4
aaab
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    2 0
4 0
   
   
   
   

 

Source

2015 ACM/ICPC Asia Regional Changchun Online

 

Recommend

hujie   |   We have carefully selected several similar problems for you:   5467  5466  5463  5462  5461 

 

拖到这么晚才来补题。。题意就是找一个同构串 让它字典序最大 这个串可以从原串任意位置出发 顺时针或逆时针转一圈

把串拷出来一个逆串 或者string直接用reserve方法 正逆都跑一遍最大表示 改一下最小表示的比较符号即可 正串找到的就是最左端 逆串找到的是逆串最左端 也就是正串最右端 用KMP算出正串最小循环节(len-next[len])%len == 0? len/next[len]: 1; 对最小循环节取余即可

需要注意的是如果两个方向得到的串字典序一样 输出下标靠左的 如果下标一样 输出顺时针的

 关于最小(大)表示法 善用百度。。

代码如下:

#include <bits/stdc++.h>

using namespace std;

char st1[23333],st2[23333];

int Maximze(char *s,int len)//最大表示法
{
    int i,j,k,t;

    i = k = 0;
    j = 1;
    while(i < len && j < len && k < len)
    {
        t = s[(j+k)%len] - s[(i+k)%len];
        if(!t) ++k;
        else
        {
            if(t > 0) i = i+k+1;
            else j = j+k+1;
            if(i == j) ++j;
            k = 0;
        }
    }
    return min(i,j);
}

int cmp(char *str1,int s1,char *str2,int s2,int len)//两方向字典序比较
{
    for(int i = 0; i < len; ++i, s1 = (s1+1)%len, s2 = (s2+1)%len)
    {
        if(str1[s1] > str2[s2]) return 1;
        else if(str1[s1] < str2[s2]) return -1;
    }
    return 0;
}

int Next[23333];
void Get(char *s,int len)//KMP
{
    int i,j;
    j = Next[0] = -1;
    i = 1;
    while(i < len)
    {
        while(j != -1 && s[i] != s[j])
        {
            j = Next[j];
        }
        Next[i] = ++j;
        ++i;
    }
}

//void Print(int len)
//{
//    for(int i = 0; i < len; ++i) printf("%d ",Next[i]);
//    puts("");
//}

int Solve(char *s,int len)
{
    Get(s,len);
    if(len%(len-Next[len-1])) return len;
    else return len-Next[len-1];
}

int main()
{
    int t,n,a,b,c,k;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d %s",&n,st1);
        for(int i = 0; st1[i]; ++i)//求逆串
            st2[n-i-1] = st1[i];
        st2[n] = 0;
        //puts(st2);
        a = Maximze(st1,n);//正串最大表示
        b = Maximze(st2,n);//逆串最大表示
        //printf("%d %d\n",a,b);
        k = cmp(st2,b,st1,a,n);//比较两个最大表示字典序 1:b>a -1:b<a 0:a=b
        if(k > 0)
        {
            printf("%d 1\n",(n-b-1)%Solve(st1,n)+1);
            //Print(n);
        }
        else if(k < 0)
        {
            printf("%d 0\n",a+1);
        }
        else
        {
            b = (n-b-1)%Solve(st1,n)+1;
            a++;
            if(a <= b) printf("%d 0\n",a);
            else printf("%d 1\n",b);
            //Print(n);
        }
    }
    return 0;
}

【1003】 Aggregated Counting (找规律+打表)

Aggregated Counting

Time Limit: 1500/1000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 508    Accepted Submission(s): 226

Problem Description

Aggregated Counting Meetup (ACM) is a regular event hosted by Intercontinental Crazily Passionate Counters (ICPC). The ICPC people recently proposed an interesting sequence at ACM2016 and encountered a problem needed to be solved.

The sequence is generated by the following scheme.
1. First, write down 1, 2 on a paper.
2. The 2nd number is 2, write down 2 2’s (including the one originally on the paper). The paper thus has 1, 2, 2 written on it.
3. The 3rd number is 2, write down 2 3’s. 1, 2, 2, 3, 3 is now shown on the paper.
4. The 4th number is 3, write down 3 4’s. 1, 2, 2, 3, 3, 4, 4, 4 is now shown on the paper.
5. The procedure continues indefinitely as you can imagine. 1, 2, 2, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6, 6, . . . .

The ICPC is widely renowned for its counting ability. At ACM2016, they came up with all sorts of intriguing problems in regard to this sequence, and here is one: Given a positive number  n , First of all, find out the position of the last  n  that appeared in the sequence. For instance, the position of the last 3 is 5, the position of the last 4 is 8. After obtaining the position, do the same again: Find out the position of the last (position number). For instance, the position of the last 3 is 5, and the position of the last 5 is 11. ICPC would like you to help them tackle such problems efficiently.

 

Input

The first line contains a positive integer  T,T≤2000 , indicating the number of queries to follow. Each of the following  T  lines contain a positive number  n(n≤109)  representing a query.

 

Output

Output the last position of the last position of each query  n . In case the answer is greater than  1000000006 , please modulo the answer with  1000000007 .

 

Sample Input

   
   
   
   

    
    
    
    3
3
10
100000
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    11
217
507231491
   
   
   
   

 

Source

2015 ACM/ICPC Asia Regional Changchun Online

 

Recommend

hujie   |   We have carefully selected several similar problems for you:   5467  5466  5463  5462  5460 

 

给出数列是1 2 2 3 3 4 4 4 5 5 5 6 6 6 6 7 7 7 7 8 8 8 8 9*5 10*5 11*5 12*6 13*6 14*6 15*6 16*7...

发现什么了么 没错 从1~k 每个数有一个管辖范围 即管辖范围内的数会出现k次

1 [1,1]

2 [2,3]

3 [4,5]

4 [6,8]

5 [9,11]

可以发现 对于第i个区域[a,b] 第a~b个区域内有i个数 即 3 [4,5] 导致 4 {6,7,8} 5{9,10,11}

即遍历到区域3[4,5] 让 4~5个取余分别为 range[4] = range[4-1]+3 range[5] = range[5-1]+3 range存放区域上限 这样就可以一直递推出影响到1e9的区域(range[k] >= 1e9)

同时由于类似关系的传递 每个管辖范围又会继续往下影响 即i -> last[i] -> last[last[i]]

last[i] = last[i-1]+range[i]

last[last[i]] = last[last[i-1]] + range[last[i]];

新开一个数组ans[i] 表示last[last[i]]影响的区间的上限

1 [1,1]  1]

2 [2,3] 11]

3 [4,5] 38]

4 [6,8] 122

5 [9,11] 272

6 [12,15] 596

可以得出 ans[i] = ans[i-1]+∑(last[i-1],last[i]]*i 即ans存的就是last[i] 最后一次出现的位置

这样last[i]表示受第i个数影响的区间 ans表示该区间映射到的受影响区间 找出规律就很好打表了

每次给个n二分找到他所在的last区间 然后从对应ans[pos]递减出n对应的答案即可

代码如下:

#include <bits/stdc++.h>
#define ll long long
#define mod 1000000007

using namespace std;

int ans[500000];
int post[500000];
int tp;

ll cal(ll a)//找∑(1~a)
{
    return a&1? (a+1)/2*a: a/2*(a+1);
}

int binsearch(int l,int r,int x)//二分找第一个大于等于x的区间
{
    int ans;
    while(l <= r)
    {
        int mid = (l+r)>>1;
        if(x <= post[mid])
        {
            ans = mid;
            r = mid-1;
        }
        else l = mid+1;
    }
    return ans;
}

int main()
{
    post[1] = 1;
    ans[1] = 1;
    post[2] = 3;
    ans[2] = 5;
    tp = 3;
    for(int i = 2, j = 3; i < tp; ++i)
    {
        while(j <= post[i] && post[tp-1] < 1000000000)//n <= 1e9 所以只需找到post[tp] <= 1e9即可 i影响区间[j,post[i]]
        {
            post[tp] = post[tp-1]+i;
            ++j;
            ++tp;
        }
        ans[i] = (ans[i-1]+(((cal(post[i])-cal(post[i-1]))%mod)*i)%mod)%mod;//ans[i] = ans[i-1] + (∑(1~post[i])-∑(1~post[i]))*i
    }

    int t,n,id;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        id = binsearch(1,tp-1,n);//二分找到第一个大于等于n的区间
        printf("%d\n",(ans[id]-((cal(post[id])-cal(n))*id)%mod+mod)%mod);//ans[i] - (∑(1~post[i])-∑(1~n)) 即为n对应的答案
    }

    return 0;
}