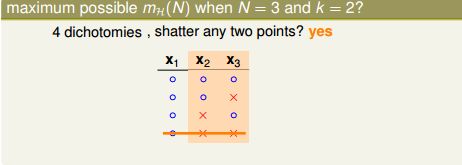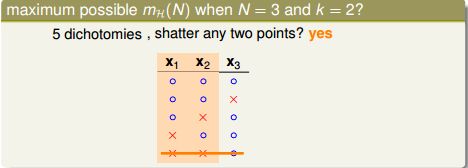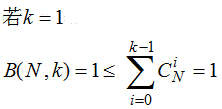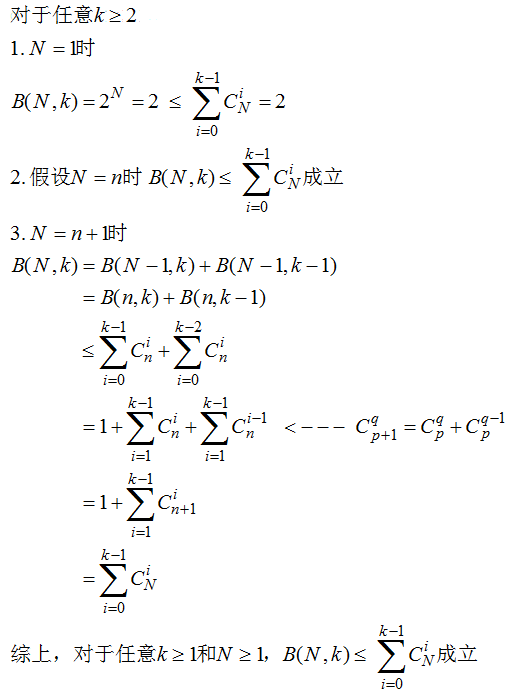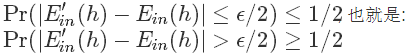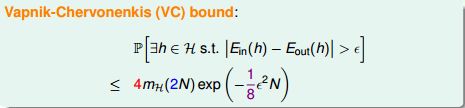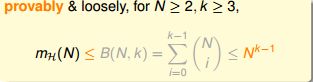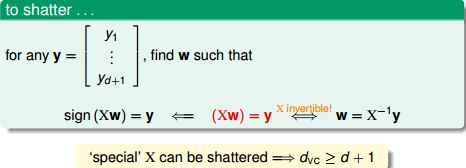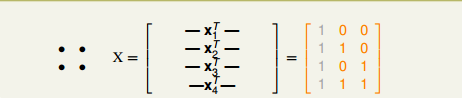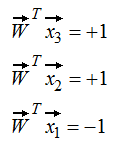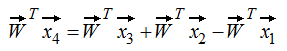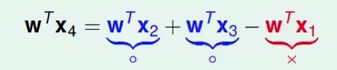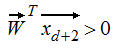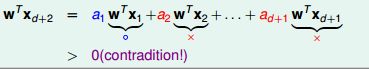NTU-Coursera机器学习:VC Bound和VC维度
Break Point 对成长函数的限制
上一讲重点是一些分析机器学习可行性的重要思想和概念,尤其是生长函数(growth function) 和突破点(break point) 的理解(上一节提到的4个成长函数):
假设对于一个问题,minimum break point k = 2(对于任意2个输入,H不能穷尽所有划分),基于该条件我们做出推论:
即当 N=2 时,成长函数一定 < 2^2=4,所以此时成长函数的 maximum possible value = 3。
当 N=3 时,我们看看成长函数的 maximum possible value 等于多少?
任意3个输入(x1, x2, x3),我们一定能找到以下3个合法的划分:
在寻找更多划分之前,我们要明确一点就是因为k=2,所以(x1, x2, x3)中任意2个点都不能被shatter,所以下面这个划分不可能出现,因为(x2, x3)所有4种可能的划分被穷尽了:
但是接下来的划分就可能了:
再之后,你发现不论再寻找什么划分,总有两个点被shatter:
所以,N=3时成长函数的maximum possible value就是 4 了。而且 4 << 2^3=8。综上我们发现,当 N > break point k,成长函数的maximum possible value显著下降并远小于 2^N。
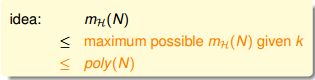
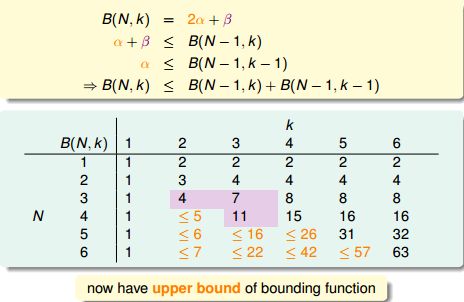
上一节课最后提出了一个猜测:如果下面的不等式成立,则猜测一定成立:
边界函数 Bounding Function(成长函数的上限)
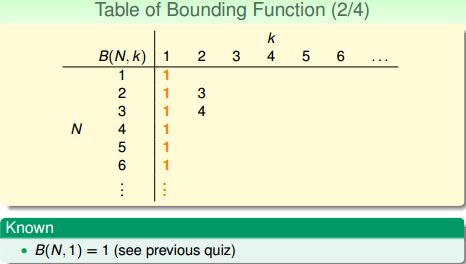
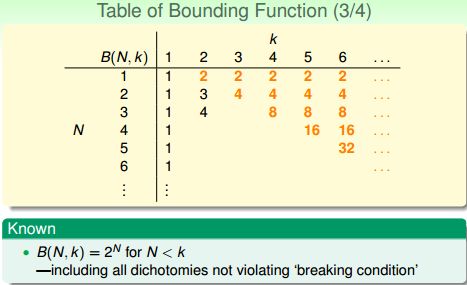
边界函数 Bounding Function B(N,k) 的定义:所以有:
当k=1时,给定任意N个输入,只能有一种划分的可能,因为任何第二种划分都会导致有一个点被shatter,这与k=1相悖,所以:
当 N<k 时,N个输入一定都能被shatter,所以 B(N,k)=2^N:
当 N=k时,首次出现N个输入不能被Shatter,所以 B(N,k)=2^N - 1 一定没错:
综上,在确定B(N,k)的过程中我们已经把软柿子都捏了,现在讨论N>k的情况。
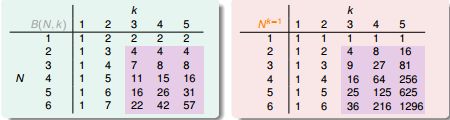
根据上图,B(3,2)=B(2,1)+B(2,2)=1+3=4;B(3,3)=B(2,2)+B(2,3)=3+4=7........
我们猜测 B(N,k) 与 B(N-1, k-1) + B(N-1, k) 也许有关系。
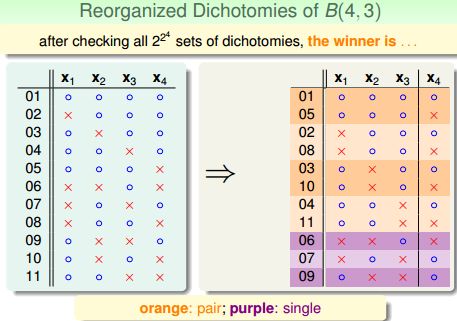
以B(4,3)为例,4个输入中任意3个都不能被shatter,用一个简单的程序遍历所有2^16个划分组合得到B(4,3)=11。

那些数学家们把这11个划分很鸡贼的分成两组(╮(╯▽╰)╭):
其中橙色的划分总能找到自己相似的“伴侣”,它与“伴侣”的(x1, x2, x3)相等,x4相反,有 2α 个;
紫色的划分总是“单身”,他找不到那个(x1, x2, x3)与它相等的“伴侣”,有 β 个。所以:
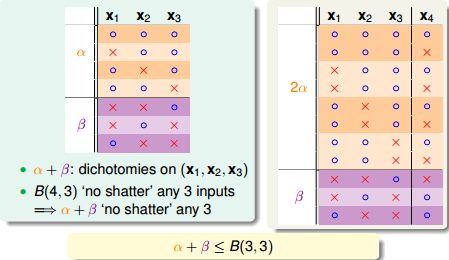
由于k=3,所以(x1, x2, x3)不能被shatter:
![]()
由于x4成对,且(x1, x2, x3, x4)不能shatter任意3个,所以(x1, x2, x3)不能shatter任意2个:
![]()
所以:
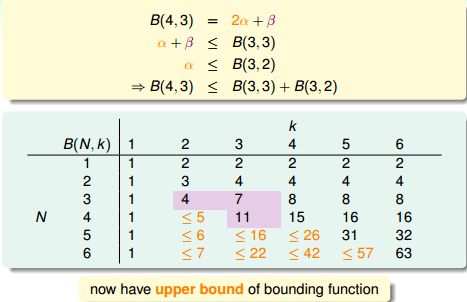
最终
边界函数的成长性为O(N^(k-1))。
======PS:上图中不等式可以用数学归纳法证明:(证明来自课程论坛ID是:Kai-Chi Huang)=====
实际上,不等式中的等号是恒成立的,证明如下:
======================================
对 VC Bound 的图像化证明
把备选函数集H中备选函数的数量M用成长函数代替,我们得到:我们看看这些多出来的系数都是怎么来的。
====PS:(下述证明过程来自课程论坛 by @hsiao-fei liu)================
首先,E-out(h)衡量的是h在全体输入上的错误,全体输入包含了未知的无限多个输入,所以我们想在训练数据集D之外再搞一个测试数据集D',然后用E'-in(h)代替E-out(h),我们把D'叫做 Ghost Data(鬼魂数据?幻影数据?what ever..)。
如果存在h在D上使得
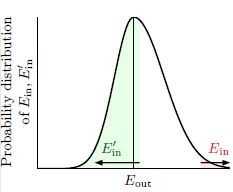
那么有很大概率使得h在D'上得到的错误 E'-in(h)与E-out(h)的距离相比E-in(h)与E-out(h)应该更近:
结合图片解释就是,样本犯错的比例有很大的概率接近全体犯错的比例,所以下面的不等式成立:
![]()
因为
![]()
所以以上这两个事件没有交集,故:
![]()
综合不等式(1)和(2)得到:
所以
=======================================================
上述不等式两边乘以2,右侧是事件【BAD】,左侧是事件发生概率的一个上边界,如果我们用去重后的Union Bound拓展这个边界,得到:
进一步,做一个等效替换:
相当于我们关心D上的错误与(D+D')上的错误之间的差距,上述不等式变成:
这就是VC Bound:
它提供了一个对机器学习结果可靠性的衡量,因为成长函数是N的多项式,所以BAD事件发生的概率随着N的增大而显著下降。需要强调的是,以上所讲的只适用于二元分类问题,因为我们在推导 break point、成长函数和边界函数时一直都基于二元分类这一前提.
VC Dimension的定义
我们知道dichotomies数量的上限是成长函数,成长函数的上限是边界函数:
边界函数的上限就是N^(k-1)了:
于是我们得到了上限(成长函数)的上限(边界函数)的上限........
所以VC Bound可以改写成:
复习结束,下面我们定义VC Dimension:
用中文讲,对于某个备选函数集H,VC Dimension就是它所能shatter的最大数据个数N。
VC Dimension = minimum break point - 1。
所以在VC Bound中,(2N)^(k-1)可以替换为(2N)^(VC Dimension)。
VC Dimension与学习算法A,输入分布P,目标函数f均无关。
PLA的VC Dimension
1D的PLA最多shatter2个点,所以VC Dimension = 2;
2D的PLA最多shatter3个点,所以VC Dimension = 3;
所以dD的PLA,VC Dimension会不会等于d+1?

要证明这一点,只需证明:
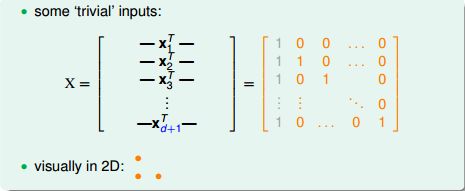
(1) 证明VC Dimension≥d+1,只需证明H可以shatter某些d+1个输入。我们刻意构造一组d+1个输入:
第一列灰色的1是对每个输入提高1维的操作,这个是一个d+1维的方阵,对角线全部是1,所以该矩阵可逆。对于任意一种输出,我们总能找到一个备选函数使得:
即这一组输入的所有dichotomies都被穷尽了,所以VC Dimension≥d+1得证。(2) 证明VC Dimension≤d+1,只需证明H不能shatter任何d+2个输入。在2D情形下构造一组4个输入:
所以 x4 = x3 + x2 - x1。
如果前3个输出是:
那么第4个输出是多少?
如果有一个备选函数W,使得其在x1,x2,x3上的输出的符号与方程中的符号相同:
那么一定有:
所以H不能shatter 2+2=4个输入。
推广到d维:

任何d+2个数据作为输入,即使升了一维之后,输入矩阵的行数(d+2)依然大于列数(d+1),所以矩阵各行是线性相关的,即x(d+2)能用x(d+1),......,x2,x1的线性组合来表示。
我们假设H可以shatter d+2个输入,那么我们一定能找到一个W,使得x(d+1),......,x2,x1对应的输出的符号与他们在线性表达式中的系数符号相同:
所以:
之前的假设是错的,H不能shatter d+2个输入。所以VC Dimension≤d+1得证。
综合(1)(2),对于d-D PLA,其VC Dimension=d+1。
VC Dimension的物理意义
在教程中这么说:即VC Dimension是备选函数集H的“能力”。“能力”越大,H对数据的划分就越细致。
例如,从Positive Ray到Positive Interval,自由变量从1个变成了2个,VC Dimension从1变成了2,H变得更强大。
在VC Dimension与备选函数集大小M基本正相关:

深入理解VC Dimension
VC Bound:所以GOOD事件:| E-in(h) - E-out(h) ≤ ε |可以改写成:
我们最终希望E-out越小越好,所以上面的不等式中可以只关心上界。我们把根号项看做一种惩罚,它拉大了E-in与E-out之间的距离,这个惩罚与“模型复杂度”有关,模型越复杂,惩罚越大:
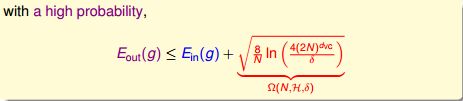
上面的”模型复杂度“ 的惩罚(penalty),基本表达了模型越复杂(VC维大),Eout 可能距离Ein 越远。下面的曲线可以更直观地表示这一点:一图胜千言,可以看出随着模型复杂度的增加,E-in与E-out两条曲线渐行渐远。
如果VC Dimension太大,模型复杂度增加,E-in与E-out偏离;
如果VC Dimension太小,虽然E-in≈E-out,但H不够给力,很难找到不犯错(或很少犯错)的h。
-----------------------------------------------------------------------------------------------------------
VC Bound提高了数据复杂度。
用一个简单的数学题就能说明:
你帮老板分析股票数据,老板说E-in与E-out差距最大为ε=0.1;置信度为90%,即δ=0.1;所用模型的VC Dimension = 3。你用程序算了一番,发现:

于是你向老板汇报,请给我29300条数据作为训练集、29300条作为测试集,我就能达到你的要求,如果想万无一失,200000条数据是起码的。本来被老板逼死的节奏,现在要把老板逼死了,哪来这么多数据?
本题中:
need N ≈ 10000 * VC Dimension
而实际应用中,需要的数据量在10倍VC Dimension左右。
为什么VC Bound会这么宽松,以至于过多估算数据量?
因为VC Bound对数据分布、目标函数、备选函数集、学习算法都没有要求,它牺牲了部分精确性,换来了无所不包的一般性。这使得VC Bound具有哲学意义上的指导性。即便如此,VC Dimension & VC bound 依然是分析机器学习模型的最重要的理论工具。
关于Machine Learning更多讨论与交流,敬请关注本博客和新浪微博songzi_tea.