线性回归,偏差、方差权衡
转:http://www.cnblogs.com/LeftNotEasy/archive/2010/12/19/mathmatic_in_machine_learning_2_regression_and_bias_variance_trade_off.html
版权声明:
本文由LeftNotEasy所有,发布于http://leftnoteasy.cnblogs.com。如果转载,请注明出处,在未经作者同意下将本文用于商业用途,将追究其法律责任。如果有问题,请联系作者 [email protected]
前言:
距离上次发文章,也快有半个月的时间了,这半个月的时间里又在学习机器学习的道路上摸索着前进,积累了一点心得,以后会慢慢的写写这些心得。写文章是促进自己对知识认识的一个好方法,看书的时候往往不是非常细,所以有些公式、知识点什么的就一带而过,里面的一些具体意义就不容易理解了。而写文章,特别是写科普性的文章,需要对里面的具体意义弄明白,甚至还要能举出更生动的例子,这是一个挑战。为了写文章,往往需要把之前自己认为看明白的内容重新理解一下。
机器学习可不是一个完全的技术性的东西,之前和部门老大在outing的时候一直在聊这个问题,机器学习绝对不是一个一个孤立的算法堆砌起来的,想要像看《算法导论》这样看机器学习是个不可取的方法,机器学习里面有几个东西一直贯穿全书,比如说数据的分布、最大似然(以及求极值的几个方法,不过这个比较数学了),偏差、方差的权衡,还有特征选择,模型选择,混合模型等等知识,这些知识像砖头、水泥一样构成了机器学习里面的一个个的算法。想要真正学好这些算法,一定要静下心来将这些基础知识弄清楚,才能够真正理解、实现好各种机器学习算法。
今天的主题是线性回归,也会提一下偏差、方差的均衡这个主题。
线性回归定义:
在上一个主题中,也是一个与回归相关的,不过上一节更侧重于梯度这个概念,这一节更侧重于回归本身与偏差和方差的概念。
回归最简单的定义是,给出一个点集D,用一个函数去拟合这个点集,并且使得点集与拟合函数间的误差最小。
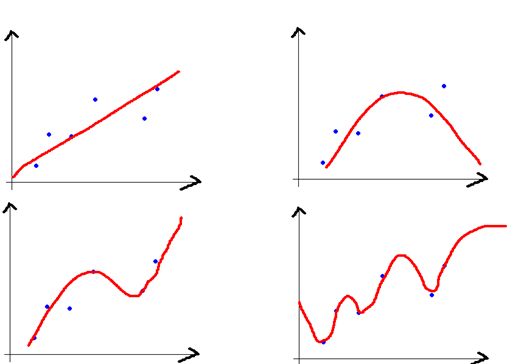 上图所示,给出一个点集(x,y), 需要用一个函数去拟合这个点集,蓝色的点是点集中的点,而红色的曲线是函数的曲线,第一张图是一个最简单的模型,对应的函数为y = f(x) = ax + b,这个就是一个线性函数,
上图所示,给出一个点集(x,y), 需要用一个函数去拟合这个点集,蓝色的点是点集中的点,而红色的曲线是函数的曲线,第一张图是一个最简单的模型,对应的函数为y = f(x) = ax + b,这个就是一个线性函数,
第二张图是二次曲线,对应的函数是y = f(x) = ax^2 + b。
第三张图我也不知道是什么函数,瞎画的。
第四张图可以认为是一个N次曲线,N = M - 1,M是点集中点的个数,有一个定理是,对于给定的M个点,我们可以用一个M - 1次的函数去完美的经过这个点集。
真正的线性回归,不仅会考虑使得曲线与给定点集的拟合程度最好,还会考虑模型最简单(奥卡母剃刀问题),这个话题我们将在本章后面的偏差、方差的权衡中深入的说,另外这个话题还可以参考我之前的一篇文章:贝叶斯、概率分布与机器学习,里面对模型复杂度的问题也进行了一些讨论。
线性回归(linear regression),并非是指的线性函数,也就是
x0,x1…表示一个点不同的维度,比如说上一节中提到的,房子的价钱是由包括面积、房间的个数、房屋的朝向等等因素去决定的。而是用广义的线性函数:
![]() wj是系数,w就是这个系数组成的向量,它影响着不同维度的Φj(x)在回归函数中的影响度,比如说对于房屋的售价来说,房间朝向的w一定比房间面积的w更小。Φ(x)是可以换成不同的函数,不一定要求Φ(x)=x,这样的模型我们认为是广义线性模型。
wj是系数,w就是这个系数组成的向量,它影响着不同维度的Φj(x)在回归函数中的影响度,比如说对于房屋的售价来说,房间朝向的w一定比房间面积的w更小。Φ(x)是可以换成不同的函数,不一定要求Φ(x)=x,这样的模型我们认为是广义线性模型。
最小二乘法与最大似然:
这个话题在此处有一个很详细的讨论,我这里主要谈谈这个问题的理解。最小二乘法是线性回归中一个最简单的方法,它的推导有一个假设,就是回归函数的估计值与真实值间的误差假设是一个高斯分布。这个用公式来表示是下面的样子:![]() ,y(x,w)就是给定了w系数向量下的回归函数的估计值,而t就是真实值了,ε表示误差。我们可以接下来推出下面的式子:
,y(x,w)就是给定了w系数向量下的回归函数的估计值,而t就是真实值了,ε表示误差。我们可以接下来推出下面的式子:
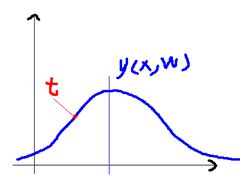
![]() 这是一个简单的条件概率表达式,表示在给定了x,w,β的情况下,得到真实值t的概率,由于ε服从高斯分布,则从估计值到真实值间的概率也是高斯分布的,看起来像下面的样子:
这是一个简单的条件概率表达式,表示在给定了x,w,β的情况下,得到真实值t的概率,由于ε服从高斯分布,则从估计值到真实值间的概率也是高斯分布的,看起来像下面的样子:
 贝叶斯、概率分布与机器学习这篇文章中对分布影响结果这个话题讨论比较多,可以回过头去看看,由于最小二乘法有这样一个假设,则会导致,如果我们给出的估计函数y(x,w)与真实值t不是高斯分布的,甚至是一个差距很大的分布,那么算出来的模型一定是不正确的,当给定一个新的点x’想要求出一个估计值y’,与真实值t’可能就非常的远了。
贝叶斯、概率分布与机器学习这篇文章中对分布影响结果这个话题讨论比较多,可以回过头去看看,由于最小二乘法有这样一个假设,则会导致,如果我们给出的估计函数y(x,w)与真实值t不是高斯分布的,甚至是一个差距很大的分布,那么算出来的模型一定是不正确的,当给定一个新的点x’想要求出一个估计值y’,与真实值t’可能就非常的远了。
概率分布是一个可爱又可恨的东西,当我们能够准确的预知某些数据的分布时,那我们可以做出一个非常精确的模型去预测它,但是在大多数真实的应用场景中,数据的分布是不可知的,我们也很难去用一个分布、甚至多个分布的混合去表示数据的真实分布,比如说给定了1亿篇网页,希望用一个现有的分布(比如说混合高斯分布)去匹配里面词频的分布,是不可能的。在这种情况下,我们只能得到词的出现概率,比如p(的)的概率是0.5,也就是一个网页有1/2的概率出现“的”。如果一个算法,是对里面的分布进行了某些假设,那么可能这个算法在真实的应用中就会表现欠佳。最小二乘法对于类似的一个复杂问题,就很无力了
偏差、方差的权衡(trade-off):
偏差(bias)和方差(variance)是统计学的概念,刚进公司的时候,看到每个人的嘴里随时蹦出这两个词,觉得很可怕。首先得明确的,方差是多个模型间的比较,而非对一个模型而言的,对于单独的一个模型,比如说:
这样的一个给定了具体系数的估计函数,是不能说f(x)的方差是多少。而偏差可以是单个数据集中的,也可以是多个数据集中的,这个得看具体的定义。
方差和偏差一般来说,是从同一个数据集中,用科学的采样方法得到几个不同的子数据集,用这些子数据集得到的模型,就可以谈他们的方差和偏差的情况了。方差和偏差的变化一般是和模型的复杂程度成正比的,就像本文一开始那四张小图片一样,当我们一味的追求模型精确匹配,则可能会导致同一组数据训练出不同的模型,它们之间的差异非常大。这就叫做方差,不过他们的偏差就很小了。这里我lsj是这样的理解:就是你的模型越复杂最后你拟合的曲线与源数据的偏差很小。相反,你的模型越简单则你拟合出的模型将会导致偏差大。总之,偏差是与源数据之间的误差。而当你的模型选得复杂的话,那么容易导致通过不同子数据集拟合出来的曲线不一样,这就是方差。那么你需要在方差和偏差直接寻找一个平衡,trade—off。
如下图所示:
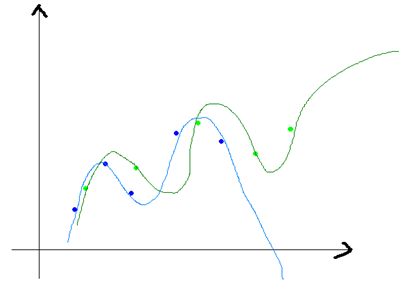 上图的蓝色和绿色的点是表示一个数据集中采样得到的不同的子数据集,我们有两个N次的曲线去拟合这些点集,则可以得到两条曲线(蓝色和深绿色),它们的差异就很大,但是他们本是由同一个数据集生成的,这个就是模型复杂造成的方差大。模型越复杂,偏差就越小,而模型越简单,偏差就越大,方差和偏差是按下面的方式进行变化的:
上图的蓝色和绿色的点是表示一个数据集中采样得到的不同的子数据集,我们有两个N次的曲线去拟合这些点集,则可以得到两条曲线(蓝色和深绿色),它们的差异就很大,但是他们本是由同一个数据集生成的,这个就是模型复杂造成的方差大。模型越复杂,偏差就越小,而模型越简单,偏差就越大,方差和偏差是按下面的方式进行变化的:
用一个很通俗的例子来说,现在咱们国家一味的追求GDP,GDP就像是模型的偏差,国家希望现有的GDP和目标的GDP差异尽量的小,但是其中使用了很多复杂的手段,比如说倒卖土地、强拆等等,这个增加了模型的复杂度,也会使得偏差(居民的收入分配)变大,穷的人越穷(被赶出城市的人与进入城市买不起房的人),富的人越富(倒卖土地的人与卖房子的人)。其实本来模型不需要这么复杂,能够让居民的收入分配与国家的发展取得一个平衡的模型是最好的模型。
最后还是用数学的语言来描述一下偏差和方差:
![]() E(L)是损失函数,h(x)表示真实值的平均,第一部分是与y(模型的估计函数)有关的,这个部分是由于我们选择不同的估计函数(模型)带来的差异,而第二部分是与y无关的,这个部分可以认为是模型的固有噪声。
E(L)是损失函数,h(x)表示真实值的平均,第一部分是与y(模型的估计函数)有关的,这个部分是由于我们选择不同的估计函数(模型)带来的差异,而第二部分是与y无关的,这个部分可以认为是模型的固有噪声。
对于上面公式的第一部分,我们可以化成下面的形式:
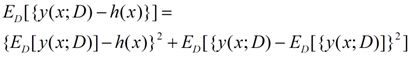 这个部分在PRML的1.5.5推导,前一半是表示偏差,而后一半表示方差,我们可以得出:损失函数=偏差^2+方差+固有噪音。
这个部分在PRML的1.5.5推导,前一半是表示偏差,而后一半表示方差,我们可以得出:损失函数=偏差^2+方差+固有噪音。
下图也来自PRML:
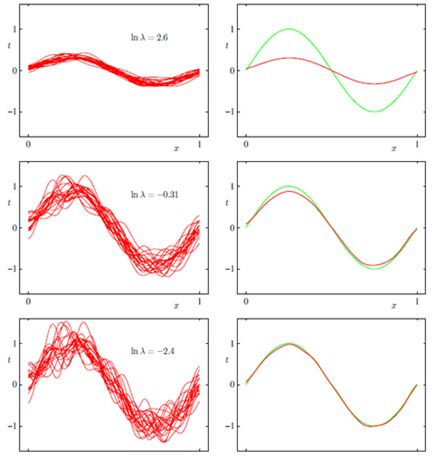
注:lsj,我们在允许一定的方差范围,同时也可以达到偏差很好。
这是一个曲线拟合的问题,对同分布的不同的数据集进行了多次的曲线拟合,左边表示方差,右边表示偏差,绿色是真实值函数。ln lambda表示模型的复杂程度,这个值越小,表示模型的复杂程度越高,在第一行,大家的复杂度都很低(每个人都很穷)的时候,方差是很小的,但是偏差同样很小(国家也很穷),但是到了最后一幅图,我们可以得到,每个人的复杂程度都很高的情况下,不同的函数就有着天壤之别了(贫富差异大),但是偏差就很小了(国家很富有)。