树和二叉树
引言
这次我们有一门数据结构的自考,还有软考,里面的很多知识都是重复的,所以我们学起来相对没有那么难。但实时总结还是很有必要的!今天我们来说说树和二叉树。
概念
树
相关概念
结点的度:树上任一结点所拥有的子树的数目称为该结点的度。
叶子:度为0的结点称为叶子或终端结点。
树的度:一棵树中所有结点的度的最大值称为该树的度。
结点的层次:从根开始算起,根的层次为1,其余结点的层次为双亲的层次加1.
树的高度:一棵树中所有结点层次数的最大值称为该树的高度或深度。
有序树:若树种各结点的子树从左到右是有次序的,不能互换,称为有序树。有序树中最左边子树的根称为第一个孩子,左边第i个子树的根称为第i个孩子。
无序树:若树中各结点的子树是无次序的,可以互换,则称为无序树。
树的遍历:访问树中的每个结点,且每个结点仅被访问一次。可分为:先序遍历、中序遍历、后序遍历和层次遍历。
二叉树
二叉树是n个(n≥0)个结点的有限集合,它或者是空树(n=0),或者是由一个根结点及两棵不相交的且分别称为左、右子树的二叉树所组成。
树和二叉树之间的主要区别是:二叉树中结点的子树要区分左子树和右子树,即使在结点只有一颗子树的情况下,也要明确指出该子树是左子树还是右子树。另外,二叉树结点最大度为2,而树中不限制结点的度数。。
二叉树的性质:
1、 二叉树第i层(i≥1)上最多有2^(i-1)个结点。
2、高度为k 的二叉树最多有2^k-1.
3、 对于任何一棵二叉树,若其终端结点数为n0,度为2的结点数为n2,则n0=n2+1。
4、 具有n个结点的完全二叉树的深度为┗log2n┘+1.
5、 对一棵有n个结点的完全二叉树的所有结点按层次自上而下、自左至右进行编号,对于任一个结点i(1≤i≤n)有:
① 若i=1,则结点i是二叉树的根,无双亲;若i>1,则其双亲为i/2。
② 若2i>n,则结点i没有左孩子,否则其左孩子为2i。
③ 若2i+1>n,则结点i没有右孩子,否则其右孩子为2i+1。
例如:
二叉树的遍历:
分为先序遍历、终须遍历和后序遍历。这里是根据根的顺序说的。
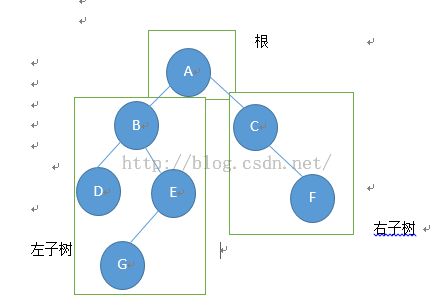
我们根据上面的二叉树来做个例子:
1、 先序遍历(根左右)
先访问根,然后访问左子树,最后访问右子树。
所以顺序是:ABDEGCF
2、 中序遍历(左根右)
先访问左子树,然后访问根,最后访问右子树。
所以顺序是:DBGEACF
3、 后序遍历(左右根)
先访问左子树,然后访问右子树,最后访问根。
所以顺序是:DGEBFCA
其他二叉树
线索二叉树
当n 个结点的二叉树采用二叉链表做存储结构,则链表中必然有n+1个空指针域,利用这些空指针域存放指向结点在某种遍历次序下的前驱和后继结点的指针。
加上线索的二叉树称为线索二叉树。线索就是指向结点前驱和后继的指针。
最优二叉树
又称为哈夫曼树,是一类带权路径长度最短的树。
树的路径长度是从树根到每一个叶子之间的路径长度之和。带权路径长度为从该结点到树根之间的路径长度与该结点权值的乘积。
平衡二叉树
是一棵空树或它的左右两个子树的高度的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
当平衡二叉树失去平衡了,我们可以采用LL型单向右旋平衡、RR型单向左旋平衡处理、LR型先左后又双向旋转平衡、RL型先右后左双向旋转平衡处理。不过这几种处理还有点蒙,正在研究当中……请大家不吝赐教!
总结
有的知识,你总觉得自己会了,但是你不去总结,其实还是什么都不会,当时只是眼熟而已。总结真的很有必要,给自己留一点总结的时间,同时,给自己的知识一个沉淀的过程!fighting~