概率统计随记(显著性检验 置信区间等）



显著性检验（significance test）就是事先对总体（随机变量）的参数或总体分布形式做出一个假设，然后利用样本信息来判断这个假设（备则假设）是否合理，即判断总体的真实情况与原假设是否有显著性差异。或者说，显著性检验要判断样本与我们对总体所做的假设之间的差异是纯属机会变异（随机产生的），还是由我们所做的假设与总体真实情况之间不一致所引起的。 显著性检验是针对我们对总体所做的假设做检验，其原理就是“小概率事件实际不可能性原理”来接受或否定假设。
上面的话是抄来的，如果不是很好理解，我们来看几个例子：
A）抛硬币试验
      我们知道如果硬币是均匀的，则抛硬币试验服从二项分布，如果抛100次，出现正面和反面的次数应该差不多。但如果实际抛的结果正反面出现的次数差别很大呢？这时候我们就要考虑怀疑假设了。通过这种假设和结果检验，给我们提供了一种判断手段（硬币是不是均匀的）。
     原假设H0：硬币是均匀的
    备选假设H1:硬币不是均匀的.
B）测量身高值（这个可以扩充为任何参数值）
     我们知道，如果测量身高的误差产生是随机的，那么标准化的误差应该服从N(0，1）分布。如果实际的误差非常大，那么也可以怀疑我们的假设（误差是随机产生的）有问题。
    原假设H0：测量的误差是随机的
    备选假设H1:测量的误差不是随机的
C）总体均值
    如果随机变量x1,x2,...,xn的是相互独立的，那么这些样本的均值m将服从正态分布N(μ，δ）,如果样本结果均值m与μ的差异非常大，当然也可以怀疑假设出问题了.
    原假设H0：随机变量序列x1,x2,...,xn是相互独立的
    备选假设H1:随机变量序列x1,x2,...,xn不是相互独立的.

从上面的例子我们可以看出，可以利用样本信息来判断我们的假设是否合理。但问题随之而来：

A）什么时候我们可以接受原假设，什么时候我们可以否定原假设呢？
      比如抛硬币试验，有4次试验结果：
     1) 60次正 40次反 差异20
     2) 80次正 20次反 差异60
     3) 95次正 5次反  差异90
     4) 99次正 1次反  差异98
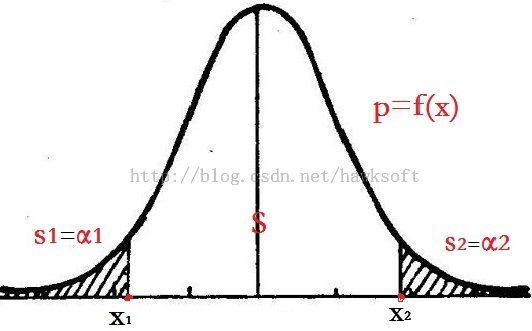
     这个判断就很主观，不怎么好做，而且不直观。我们知道如果n比较大的话，二项分布近似于正态分布.如上面图示，如果设k为试验中的正面次数，P{x1<= k <=x2}=95%==》P{k>=95}的概率小于5%(这个很容易推算，正态分布是对称的，s1+s2的概率就略小于5%（x1,x2是2倍标准差位置），利用频率收敛于概率,可以得出100*5%=5次），这个概率已经比较小了，基本上不可能发生（小概率事件实际不可能性原理）。也就是说100次中，出现5次在落点在x1和x2之外的概率已经非常小。但3)和4)确实发生了，这说明什么呢？说明原假设是不可接受的。上面的s1+s2就是显著性水平，显著性水平α是一个概率，α=s1+s2。需要注意的是，这个α的值的选取是经验性的，一般取0.1,0.05,0.01.
一般来说，如果比这个α还小概率的事件确实发生了，那么就可以否定原假设（更合理的叫拒绝，后面会谈到为什么），因为我们选取的是5%,试验3落在[x1,x2]之外的概率为5%,试验4落在[x1,x2]之外的概率为1%。为了谨慎起见，我们在拒绝原假设时一般都要求样本概率p小于α.因此如果实际试验出现的是第4)种情况，则可以拒绝原假设。
B）接受原假设，假设就一定为真？否定了原假设，原假设就一定不是真的？
     上面说否定原假设是不合理的，应该叫拒绝原假设，为什么呢？大家可以看出，概率在怎么小，毕竟也是概率，因此在统计中是无绝对的。实际上，上面的分析中，α=5%,说k明落在[x1,x2]之间的概率应该是95%，现在k没落在[x1,x2]之间，你也只能说有95%的把握可以拒绝原假设，换一种说话就是拒绝原假设的支持度只有95%，95%就是置信度，一般置信度=1-α。p值是实际计算出来的概率值。如果p<α则拒绝原假设，如果p>=α则接受原假设。
      注意：拒绝原假设，原假设也不一定为假，接受原假设，原假设也不绝对为真，需要用概率的思维来看待。所以才会加个可信度（置信度）。

总结：从上面的图可以看出，在某个假设为真的情况下，样本X服从概率密度为f(x)的分布，样本X的某个参数值θ:P{x1<=θ<=x2}=1-α,如果α比较小，则表示θ落在[x1,x2]的概率非常大，等价于θ落在区间[x1,x2]之外的概率非常小，根据小概率事件实际不可能性原理，如果样本X的参数θ的观察p值（实际概率）小于α,我们就可以拒绝原假设。这个α值是根据经验取的。而且根据f(x)我们可以算出[x1,x2]区间，这个区间就是置信区间。下面是常用的置信区间计算：

分布较z检验，t检验,x平方检验。

需要注意的是置信度和置信区间与显著性检验还是有区别的，显著性检验关注的是对总体的参数或者分布的假设是否合理，而置信度和置信区间，关注的是样本值和总体值（测量值和真实值）之间的关系。比如一个样本的测量值是u,如果置信度为95%，置信区间是[x1,x2],则表示样本的真实值值有95%的置信度（可靠性）落在[x1,x2]之间。当然x1,x2是u的函数。一般可以利用u算出来。常用的置信区间计算可参考上面的图中所示。

后记：如果总体的概率密度为p=f(x),我们假设样本服从总体，那么本质上来说，显著性检验就是利用下图中的阴影部分的概率α（对应于面积s1+s2，也叫截尾面积），如果α很小，则可以认为事件不可能发生在区间[x1,x2]之外，但如果事件落在区间[x1,x2]之外实际发生了，而且其实际观测概率p比α还小，这就说明样本事件可能不是来自于总体。即样本与总体是有显著差异的。当然，α可以看作是我们认为样本与总体有显著差异性的可接受的最小值(底线）。如果事件实际落在[x1,x2]之外的概率p，还比α小（α这就已经比较小了，我们已经认为事件不可能发生了，但样本还在更小的概率p下发生了,这太没天理了，突破了我们可以接受的底线），则说明差异确实存在，而且确实显著。