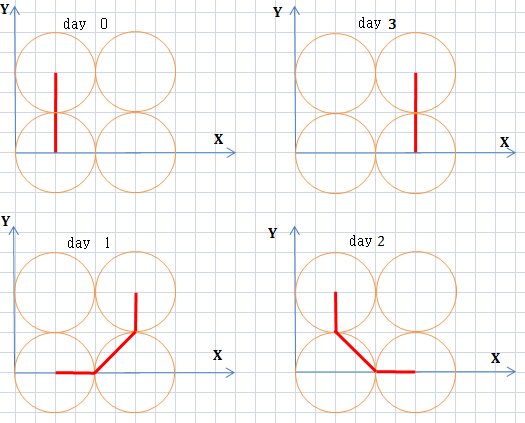CF#195(div2) B:Vasily the Bear and Fly

http://codeforces.com/contest/336/problem/B

 

One beautiful day Vasily the bear painted 2m circles of the same radiusR on a coordinate plane. Circles with numbers from1 to m had centers at points(2R - R, 0), (4R - R, 0), ..., (2Rm - R, 0), respectively. Circles with numbers from m + 1 to 2m had centers at points(2R - R, 2R), (4R - R, 2R), ...,(2Rm - R, 2R), respectively.

Naturally, the bear painted the circles for a simple experiment with a fly. The experiment continued form² days. Each day of the experiment got its own unique number from0 to m² - 1, inclusive.

On the day number i the following things happened:

1. The fly arrived at the coordinate plane at the center of the circle with number ( is the result of dividing number x by numbery, rounded down to an integer).
2. The fly went along the coordinate plane to the center of the circle number ( is the remainder after dividing number x by numbery). The bear noticed that the fly went from the center of circlev to the center of circle u along the shortest path with all points lying on the border or inside at least one of the2m circles. After the fly reached the center of circleu, it flew away in an unknown direction.

Help Vasily, count the average distance the fly went along the coordinate plane during each of thesem² days.

Input

The first line contains two integers m, R (1 ≤ m ≤ 10⁵,1 ≤ R ≤ 10).

Output

In a single line print a single real number — the answer to the problem. The answer will be considered correct if its absolute or relative error doesn't exceed10^- 6.

Sample test(s)

Input

1 1

Output

2.0000000000

Input

2 2

Output

5.4142135624

Note

Figure to the second sample

题意：给出m和r，一共有两排，每排m个圆圈，其序号确定，一共有m^2天，每天七点是 ，终点是

要求出m^2天里所走的平均路程，注意每次路程必须最短

 

思路：根据给出的条件，我们可以知道，最终所走的路线就是以每个下面圈为起点去遍历上面所有的点，当距离大于3的时候，斜线必然要走两次，当时一直卡在这里了。

 

#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <math.h>
using namespace std;

double a[100005],s[100005],ans;

int main()
{
    int i,m;
    double x = sqrt(2.0),r;
    while(~scanf("%d%lf",&m,&r))
    {
        ans = 0;
        s[0] = 0;
        a[1] = 2.0*r;//m为1时的走法
        a[2] = 2.0*r+x*r;//m为2只走一斜线
        a[3] = 2.0*r+2.0*x*r;//从下到上，要跨越的纵向距离为3，必然要斜走两次，这样才是最短
        for(i = 4; i<=m; i++)
            a[i] = a[i-1]+2*r;//除了斜走之外，全部都是直走
        for(i = 1; i<=m; i++)
            s[i] = s[i-1]+a[i];//将所有点的走法加起来
        for(i = 1; i<=m; i++)
            ans+=(s[i]+s[m-i+1]-a[1])/m;//加上每次的走法，因为s的限制，必须加上对称点再减去重复的部位
            /*这里以m为5,i为2为例，i = 2时，走法应该是：a2+a1+a2+a3+a4,即a1+2*a2+a3+a4
            s[2] = a1+a2，但是这样走不到3,4,5，加上对称点s[4] = a1+a2+a3+a4,才能得到正确的走法
            */
        printf("%.10lf\n",ans/m);
    }

    return 0;
}