给10^7个有重复的整数排序(败者树)
参考July博文:程序员编程艺术:第十章、如何给10^7个数据量的磁盘文件排序,感谢July。
给10^7个无重复的整数排序请看另一篇博文:10^7个无重复的整数排序
对于给10^7个有重复的整数排序,我们不能用位图法来做,位图法只适用于无重复的数字,那么假设我们没有足够的内存去存储这1千万个整数,我们该如何去排序呢?还是分治法,把大化为小。比如:我们可以把这1千万个整数化为10份,用10个文件存储,分别为data1.txt到data10.txt,并且我们的内存足够存储每一份数据,即每一个dataX.txt,这样,我们就可以依次对这10个文件读取进内存,并利用内部排序,如快速排序,对每一个文件进行排序,然后在对这10个有序的文件进行归并排序,这样就达到我们的要求,即对这10^7个有重复的整数排序了。
下面请看代码,我把这10^7个整数分为10份,存储在10个文件中,依次对每一个文件进行快速排序,然后在对这10个文件进行归并排序,在归并的时候,只是采用类似选择排序的方法选择最小值,故比较次数与文件成线性关系。
const int FILE_NUM = 10; const int MAX_PART = 1000000; FILE *fpreads[FILE_NUM]; int cmp(const void* a, const void *b) { return *((int*)a) - *((int*)b); } //从unsort_data.txt中读取数据 int read_data(FILE *fp, int *array, int N) { int length = 0; int num; for (int i = 0; i < MAX_PART && (EOF != fscanf(fp, "%d", &num)); i++) { length++; array[i] = num; } return length; } //打开data1.txt - data10.txt这10个文件 FILE* open_file(int count, char *mode) { FILE *fpwrite; char filename[20]; memset(filename, 0, 20); sprintf(filename, "data%d.txt", count); fpwrite = fopen(filename, mode); assert(fpwrite != NULL); return fpwrite; } //向data1.txt - data10.txt这10个文件写入排好序的数据 void write_data(int *array, int N, int count) { FILE *fpwrite = open_file(count, "w"); for (int i = 0; i < N; i++) { fprintf(fpwrite, "%d ", array[i]); } fclose(fpwrite); } //内部排序,调用10次快速排序,产生data1.txt - data10.txt这10个有序文件 void interior_sort(void) { clock_t begin = clock(); FILE *fpread = fopen("unsort_data.txt", "r"); assert(fpread != NULL); int count = 1; int *array = new int[MAX_PART]; assert(array != NULL); while (1) { memset(array, 0, sizeof(int) * MAX_PART); int length = read_data(fpread, array, MAX_PART); if (length == 0) { break; } qsort(array, length, sizeof(int), cmp); write_data(array, length, count); count++; } delete [] array; fclose(fpread); clock_t end = clock(); cout<<"10次快速排序所需时间为: "<<(end - begin)/CLK_TCK << "s"<<endl; } //对data1.txt - data10.txt这10个有序文件进行归并 void merge_sort() { clock_t begin = clock(); FILE *fpreads[FILE_NUM]; //10个文件的描述符 int data[FILE_NUM]; //10个文件的10个当前最小数据 bool flag[FILE_NUM] = {0}; //标记10个文件,是否已到EOF FILE *fpwrite = fopen("sort_data.txt", "w"); assert(fpwrite != NULL); for (int i = 0; i < FILE_NUM; i++) { fpreads[i] = open_file(i + 1, "r"); } for (int i = 0; i < FILE_NUM; i++) { fscanf(fpreads[i], "%d", &data[i]); } while (1) { int count = 0; while (count < FILE_NUM && flag[count]) { count++; } if (count == FILE_NUM) { break; } int min_data = data[count]; int index = count; for (int i = index; i < FILE_NUM; i++) //在10个文件中找最小的数 { if (!flag[i] && min_data > data[i]) { min_data = data[i]; index = i; } } fprintf(fpwrite, "%d ", min_data); if (EOF == fscanf(fpreads[index],"%d", &data[index])) { flag[index] = true; } } for (int i = 0; i < FILE_NUM; i++) { fclose(fpreads[i]); } fclose(fpwrite); clock_t end = clock(); cout<<"10路归并排序所需时间为: "<<(end - begin)/CLK_TCK << "s"<<endl; } int _tmain(int argc, _TCHAR* argv[]) { interior_sort(); merge_sort(); return 0; }
对于上述归并排序,我们可以用败者树来刷选最小值,这样比较次数就从上述的线性级降到对数级,在归并数多的情况下,效率要比上述的要好,代码如下:
//利用败者树 const int N = 10000000; const int FILE_NUM = 10; const int MAX_PART = 1000000; FILE *fpreads[FILE_NUM]; const int MIN = -1; //最小值,必须比要排序数字的最小值要小,否则出错 const int MAX = N + 1; //最大值,必须比要排序数字的最大值要大,否则出错 int cmp(const void* a, const void *b) { return *((int*)a) - *((int*)b); } //从unsort_data.txt中读取数据 int read_data(FILE *fp, int *array, int N) { int length = 0; int num; for (int i = 0; i < MAX_PART && (EOF != fscanf(fp, "%d", &num)); i++) { length++; array[i] = num; } return length; } //打开data0.txt - data9.txt这10个文件 FILE* open_file(int count, char *mode) { FILE *fpwrite; char filename[20]; memset(filename, 0, 20); sprintf(filename, "data%d.txt", count); fpwrite = fopen(filename, mode); assert(fpwrite != NULL); return fpwrite; } //向data0.txt - data9.txt这10个文件写入排好序的数据 void write_data(int *array, int N, int count) { FILE *fpwrite = open_file(count, "w"); for (int i = 0; i < N; i++) { fprintf(fpwrite, "%d ", array[i]); } fprintf(fpwrite, "%d", MAX); //在每个文件最后写入一个最大值,表示文件结束 fclose(fpwrite); } //内部排序,调用10次快速排序,产生data0.txt - data9.txt这10个有序文件 void interior_sort(void) { clock_t begin = clock(); FILE *fpread = fopen("unsort_data.txt", "r"); assert(fpread != NULL); int count = 0; int *array = new int[MAX_PART]; assert(array != NULL); while (1) { memset(array, 0, sizeof(int) * MAX_PART); int length = read_data(fpread, array, MAX_PART); if (length == 0) { break; } qsort(array, length, sizeof(int), cmp); write_data(array, length, count); count++; } delete [] array; fclose(fpread); clock_t end = clock(); cout<<"10次快速排序所需时间为: "<<(end - begin)/CLK_TCK << "s"<<endl; } //调整 void adjust(int ls[], int data[], int s) { int t = (s + FILE_NUM)/2; while (t) { if (data[s] > data[ls[t]]) { int temp = s; s = ls[t]; ls[t] = temp; } t /= 2; } ls[0] = s; } void create_loser_tree(int ls[], int data[]) { data[FILE_NUM] = MIN; for (int i = 0; i < FILE_NUM; i++) { ls[i] = FILE_NUM; } for (int i = FILE_NUM - 1; i >= 0; i--) { adjust(ls, data, i); } } void merge_sort_by_losertree() { clock_t begin = clock(); FILE *fpreads[FILE_NUM]; //10个文件的描述符 int data[FILE_NUM + 1]; //10个文件的10个当前最小数据 int ls[FILE_NUM]; //存放败者索引的节点 int index; FILE *fpwrite = fopen("sort_data_by_losertree.txt", "w"); assert(fpwrite != NULL); for (int i = 0; i < FILE_NUM; i++) { fpreads[i] = open_file(i, "r"); } for (int i = 0; i < FILE_NUM; i++) { fscanf(fpreads[i], "%d", &data[i]); } create_loser_tree(ls, data); //创建败者树 while (data[ls[0]] != MAX) { index = ls[0]; fprintf(fpwrite, "%d ", data[index]); fscanf(fpreads[index], "%d", &data[index]); adjust(ls, data, index); } for (int i = 0; i < FILE_NUM; i++) { fclose(fpreads[i]); } fclose(fpwrite); clock_t end = clock(); cout<<"10路归并排序所需时间为: "<<(end - begin)/CLK_TCK << "s"<<endl; } int _tmain(int argc, _TCHAR* argv[]) { interior_sort(); merge_sort_by_losertree(); return 0; }
未排序的数据如下:
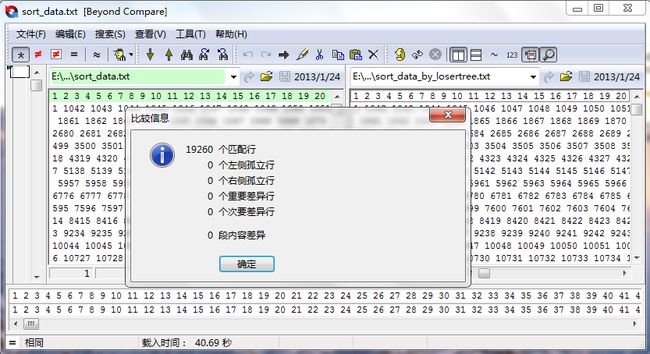
利用归并排序后的文件如下:
2013年1月24日 venow 完