机器学习实战——SVM(3/3)
前面两篇总结了线性支持向量机模型,总体来说,就是在样本输入空间下对每个维度进行线性组合之后使用符号函数判别最终的类别。第一个是理想情况下的线性可分SVM,这是第二个的近似线性可分SVM的基础。而且也是一种递进关系,是为了从数学抽象化的理想模型到现实情形的一种推广,但它们终究是一种线性模型,对于更复杂的现实情形有时候依然会难以描述,需要使用非线性模型去描述。
非线性SVM
由于现实问题的复杂性,导致训练的样本数据无法使用在输入空间 χ=Rn(或其子集或其离散集合) 下使用一个线性超平面进行分隔,对于给定的训练数据 T={(x1,y1),(x2,y2),...(xN,yN)} , xi∈χ,yi∈{−1,+1},i=1,2...N ,如果在输入空间存在一个非线性的超曲面进行分隔,将不同标记类别的训练数据分开,那么就是非线性可分的问题。
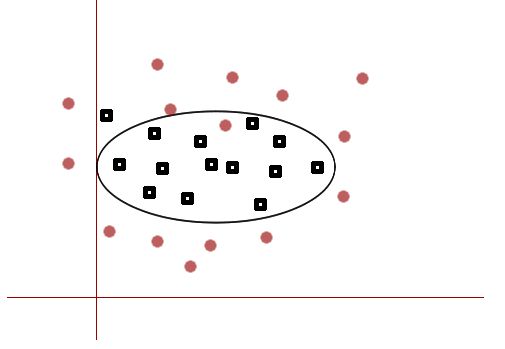
上述两类数据可以使用一个非线性的曲面进行分隔,同时为了更好地模拟现实情形,依然使用软间隔,对个别的噪声数据做出“让步”。这样也是为了防止对有限的训练数据过拟合。
实际上,如果不考虑非线性模型的复杂度和实用性,任何复杂的数据都可以使用非线性的超曲面分隔。这也是非线性SVM在前面线性SVM的基础上进行的进一步推广,涵盖了任何现实问题的最终模型。同时,将输入空间的超平面也划分为广义的非线性超曲面,那么所有的SVM模型就是统一的形式了。
空间变换与核技巧
在输入空间 χ 下的非线性分类模型不易求解,如果可以使用线性方法求解那就与前面的线性SVM的求解殊途同归了,不仅解决了非线性SVM,同时可以沿用前面求解的经验。
空间变换
解决这个问题的办法就是进行非线性的空间变换
将输入空间的 x∈χ 变换为新的空间下的 ϕ(x)∈Ω ,是的在新的空间下,所有的数据是线性可分或者近似线性可分的。这样原空间非线性问题就变为了新空间的线性问题。
但是如果寻找这样的空间变换是非常困难的,仅仅对于二次型变换就已经非常困难了,如果需要变换到更高次或者非多项式的变换,那么基本上是无法求解,更重要的是现实问题涉及到成百上千的维度,越发使得不能显式求解这样的变换,那么就需要将解决这样的问题交给核技巧了。
核技巧
核技巧(kernel trick)就是解决上述空间变换问题引入的,本质上是一个数学上解决空间变换复杂问题的一个技巧(trick),不仅仅用在这里的非线性SVM应用中,同时可以推广用到任何需要解决这种空间变换问题的统计学习问题。
核技巧首先需要定义核函数 K(x,z)
设输入空间 χ 到特征空间 Ω 存在一个变换函数
ϕ(x):χ→Ω
使得 ∀x,z∈χ ,函数 K(x,z) 满足
K(x,z)=ϕ(x)⋅ϕ(z)
那么 K(x,z) 称为核函数,式中 (⋅) 为内积。
核技巧的思想就是只定义核函数 K(x,z) ,而不定义映射函数 ϕ(x) ,将输入空间下的内积运算转换为特征空间下的内积运算,而特征空间下的内积运算就直接使用定义的核函数计算即可,这样就巧妙地绕开了显式定义空间变换困难的问题。其中特征空间的取法和核函数的取法均不唯一,可以取不同的特征空间 Ω ,同一空间下也可以取不同的核函数。
应用核技巧的非线性SVM模型
通过对之前两篇博文中两种线性模型的分析,可以看出最终都是归结为求解一个二次约束凸优化问题
目标函数中存在的唯一与 输入样本数据点相关的就是 计算任意两个样本点的内积 (xi⋅xj) 。这也正是可以使用核技巧来解决非线性SVM的关键所在。
特征空间下的线性模型
通过定义核函数 K(xi,xj) 来代替在变换后的特征空间下的任意两个数据点的内积运算,就可以得到如下的优化问题:
上述形式就和线性SVM的优化问题统一了,在新的特征空间下利用线性SVM的方法学习 线性支持向量机。这样学习了最优参数后,最终的分类决策函数就是
其中的 NΩ 是特征空间 Ω 下的样本数目。
通过上述分析可以看出,使用线性分类问题的解决办法求解了非线性的问题,其中的学习过程是 隐式地在特征空间 Ω 下进行的,不需要显式定义空间变换函数 ϕ(x) ,这就是使用核技巧解决非线性SVM问题的本质。同时这也是核技巧的魅力所在,其他类似问题同样可以使用核技巧来解决。
其实,如果选取的核函数为 线性核函数,也就是 K(xi,xj)=xi⋅xj ,那么就是 在输入空间直接学习线性SVM模型,也就对应了之前的关于线性SVM模型的讨论。因此空间变换是一种 对线性SVM的抽象,线性SVM是其中的一种特例。同时可以推广到一般特征空间下的线性SVM模型。这体现的就是数学模型 从一般(现实问题)到特殊(线性可分SVM),再从特殊(近似线性可分SVM)到一般(特征空间下的SVM)的演变过程。
核函数
给定一个函数,必须满足在特征空间下是对称的,同时,需要满足下面条件才能作为核函数使用
1, K(x,z)=K(z,x)
2, K(x,z)2≤K(x,x)K(z,z)
3, K:χ×χ→R 是对称函数, ∀xi∈χ,i=1,2...N , K(x,z) 对应的Gram矩阵K=[K(xi,xj)]N×N是半正定矩阵。
常用核函数
- 线性核函数:
K(x,z)=x⋅z原始数据是高维数据,而且每个维度都是独立的和比较重要的,就相当于在输入空间直接进行线性SVM模型的学习。
- 多项式核函数:
K(x,z)=(x⋅z+1)p对应的支持向量机是一个p次多项式分类器。
- 高斯核函数(RBF核):
K(x,z)=exp(−||x−z||22σ2)
- 余弦相似度核函数:
K(x,z)=x⋅z||x||2||z||2
还有很多其他核函数,如字符串核函数,用来度量两个字符串的相似性;Matern核函数,用在高斯过程回归的模型学习中。
模型的求解
上述包括线性SVM和使用核技巧的非线性SVM问题,最终都归结到了对偶问题的优化,是二次约束凸优化问题,这在理论上是存在全局最优解决的,可以使用最优化理论的方法进行求解,但是需要的时间是 O(N3) 。这在数据量急剧增大和维度较大时,求解过程耗时太大或者计算量无法容忍。因此需要高效算法进行求解,序列最小最优化(SMO)方法,就是Platt于1998年提出的用来高效求解的这类二次约束优化问题的,耗时只需要 O(N2) ,这在速度上的提升是非常显著的。
关于SMO算法的详细推导可以查阅相关文献容易得到,这里是对算法的一个实现。
def SMO(dataMat, labels, C, tolerance, maxIter, kernel):
objAS = AlphaStruct(dataMat, labels, C, kernel, tolerance)
ite = 0
entireSet = True; alphaPairChanged = 0
while (ite < maxIter) and ((alphaPairChanged > 0) or (entireSet)):
alphaPairChanged = 0
if entireSet:
for i in range(objAS.N):
alphaPairChanged += innerLoop(i, objAS)
print "Full set , iter : %d i: %d, pairs changed %d" % (ite, i, alphaPairChanged)
ite += 1
else:
nonBound = nonzero((objAS.alpha.A > 0) * (objAS.alpha.A < C)) [0]
for i in nonBound:
alphaPairChanged += innerLoop(i, objAS)
print "non bound, iter: %d i:%d, pairs changed %d" % (ite, i, alphaPairChanged)
ite += 1
if entireSet: entireSet = False
elif alphaPairChanged == 0: entireSet = True
print "Iteration number: %d" % ite
w = calcW(AS)
return w, objAS.b
class AlphaStruct(object):
def __init__(self, dataMat, yMat, C, kernel, tolerance):
self.X = dataMat
self.Y = yMat
self.C = C
self.tol = tolerance
self.N = dataMat.shape[0]
self.alpha = mat(zeros((self.N, 1)))
self.b = 0
self.E = mat(zeros((self.N, 2)))
self.Kernel = kernel外层while循环寻找到第一个变量后,使用内层循环寻找第二个变量,并对这两个变量依次更新。其中用到的内层循环寻找第二个变量如下:
def innerLoop(i, AS):
Ei = calcE(AS, i)
if ((AS.Y[i] * Ei < -1.0 * AS.tol) and (AS.alpha[i] < AS.C)) or\
((AS.Y[i] * Ei > AS.tol) and (AS.alpha[i] > 0)):
j,Ej = selectJ(i, AS, Ei)
alphaIold = AS.alpha[i].copy(); alphaJold = AS.alpha[j].copy()
if AS.Y[i] != AS.Y[j]:
L = max(0, AS.alpha[j] - AS.alpha[i])
H = min(AS.C, AS.C + AS.alpha[j] - AS.alpha[i])
else:
L = max(0, AS.alpha[j] + AS.alpha[i] - AS.C)
H = min(AS.C, AS.alpha[j] + AS.alpha[i])
if L == H:
print "L == H"; return 0
eta = K(AS.X[i,:], AS.X[i,:], AS.Kernel) + \
K(AS.X[j,:], AS.X[j,:], AS.Kernel) - \
2.0 * K(AS.X[i,:], AS.X[j,:], AS.Kernel)
if eta <= 0:
print "eta <= 0"; return 0;
###Update the new alpha
AS.alpha[j] = alphaJold + AS.Y[j] * (Ei - Ej) / eta
if AS.alpha[j] > H: AS.alpha[j] = H
elif AS.alpha[j] < L: AS.alpha[j] = L
updateE(AS, j)
if abs(AS.alpha[j] - alphaJold) < 0.00001:
print "j not move enough. new alpha2: %f, old alpha2 %f" % (AS.alpha[j], alphaJold); return 0
AS.alpha[i] = alphaIold + AS.Y[i] * AS.Y[j] * (alphaJold - AS.alpha[j])
updateE(AS, i)
b1 = AS.b - Ei - AS.Y[i] * K(AS.X[i,:], AS.X[i,:], AS.Kernel) * (AS.alpha[i] - alphaIold) -\
AS.Y[j] * K(AS.X[j,:], AS.X[i,:], AS.Kernel) * (AS.alpha[j] - alphaJold)
b2 = AS.b - Ej - AS.Y[i] * K(AS.X[i,:], AS.X[j,:], AS.Kernel) * (AS.alpha[i] - alphaIold) -\
AS.Y[j] * K(AS.X[j,:], AS.X[j,:], AS.Kernel) * (AS.alpha[j] - alphaJold)
if (AS.alpha[i] > 0) and (AS.alpha[i] < AS.C): AS.b = b1
elif (AS.alpha[j] > 0) and (AS.alpha[j] < AS.C): AS.b = b2
else: AS.b = (b1 + b2) / 2.0
return 1
else: return 0选取第二个变量时使用的最大步长方法,也就是选择该变量最大的。上述使用的学习到参数后,使用alpha计算出权重w,并进行最终的预测:
def calcW(AS):
ay = AS.alpha.A * AS.Y.A
w = zeros((n,1))
for i in range(AS.N):
w += AS.X[i,:].T * ay[i]
return mat(w)
def SVMClassify(model, predict):
w,b = model
res = array(predict * w) + b
res[res >= 0] = 1
res[res < 0] = -1
return res