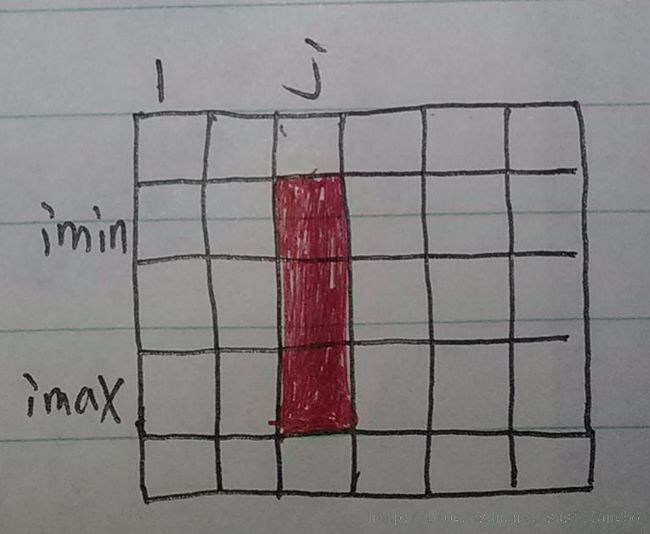上篇讲了一维的连续子数组和的最大值(编程之美错误分析),下面来分析二维数组的最大子数组和,亦称最大子矩阵,
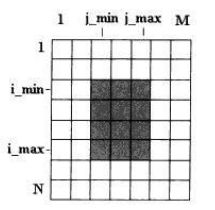
穷举法:
//求二维数组的连续子数组之和的最大值
int MaxSum(int (*array)[N])
{
int i,j;
int MaxSum=-INFINITY;//初始化
int imin,imax,jmin,jmax;
for(imin=1;imin<=N;imin++)//行的最小值
{
for(imax=imin;imax<=N;imax++)//行的最大值
{
for(jmin=1;jmin<=M;jmin++)//列的最小值
{
for(jmax=jmin;jmax<=M;jmax++)//列的最大值
MaxSum=MaxNum(MaxSum,PartSum(imin,jmin,imax,jmax));//计算子矩阵的部分和
}
}
}
return MaxSum;
}时间复杂度(N^2*M^2*O(PartSum)),如何求部分和PartSum呢?我们可以先求子矩阵的部分和,利用已经求出的部分和,来解出当前要求的矩阵的部分和,这个时候遍历求的时候复杂度就是O(1)。我们定义一个部分和数组PartSum,其中PartSum[i][[j]代表了下标(0,0),(0,j),(i,0),(i,j)包围的区间的和。
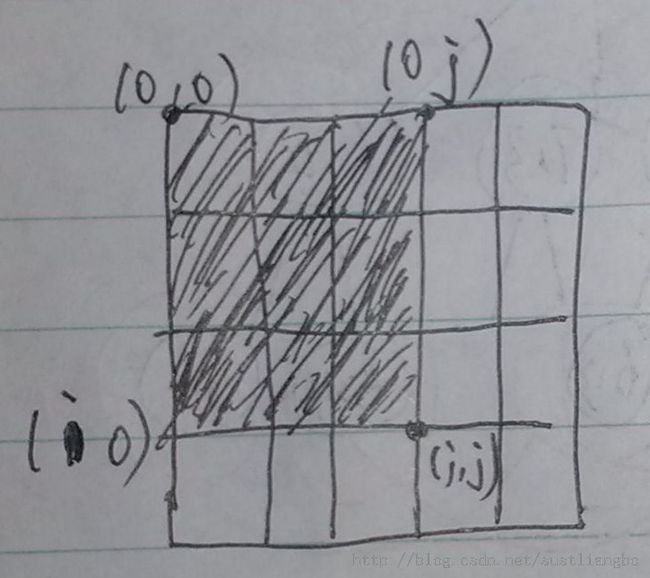
而此时下标(imin,jmin),(imin,jmax),(imax,jmin),(imax,jmax)包围的区间和就等于
PartSum[imax][[jmax]-PartSum[imin-1][[jmax]-PartSum[imax][[jmin-1]+PartSum[imin-1][[jmin-1]。如下图:
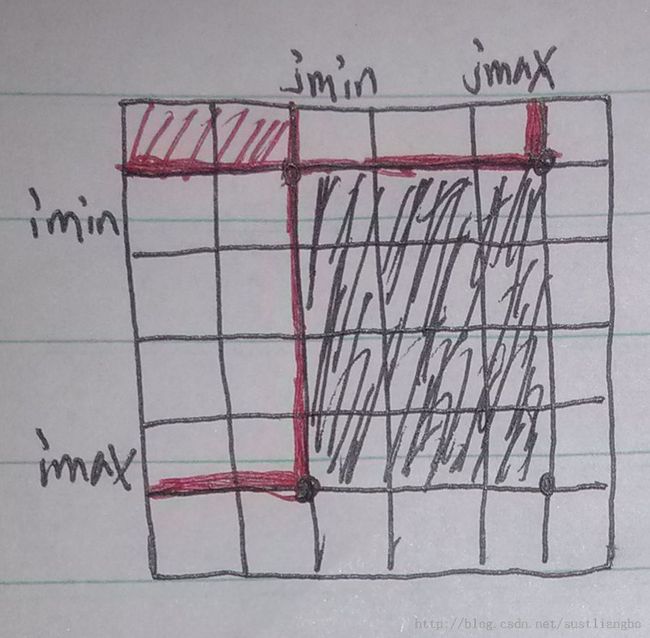
这就是我们要求的PartSum(imin,jmin,imax,jmax),接下来就是求PartSum数组了。如何求呢?对于每一个PartSum[i][[j]都不是孤立的,都是和其他的有关系的。我们要找出这个递推关系式

PartSum[i][[j]=PartSum[i-1][[j]+PartSum[i][[j-1]-PartSum[i-1][[j-1]+array[i][j],这样可以求出全部的PartSum[i][[j]。
int PartSum[N+1][M+1];
int i,j;
for(i=0;i<=N;i++)
PartSum[i][0]=0;
for(j=0;j<=M;j++)
PartSum[0][j]=0;
for(i=1;i<=N;i++)
for(j=1;j<=M;j++)
PartSum[i][j]=PartSum[i-1][j]+PartSum[i][j-1]-PartSum[i-1][j-1]+array[i-1][j-1];
OK,求得部分和之后,下标(imin,jmin),(imin,jmax),(imax,jmin),(imax,jmax)包围的区间和为:
PartSum[imax][[jmax]-PartSum[imin-1][[jmax]-PartSum[imax][[jmin-1]+PartSum[imin-1][[jmin-1]。
//求二维数组的连续子数组之和的最大值
int MaxSum(int (*array)[N])
{
int PartSum[N+1][M+1];
int i,j;
for(i=0;i<=N;i++)
PartSum[i][0]=0;
for(j=0;j<=M;j++)
PartSum[0][j]=0;
for(i=1;i<=N;i++)
for(j=1;j<=M;j++)
PartSum[i][j]=PartSum[i-1][j]+PartSum[i][j-1]-PartSum[i-1][j-1]+array[i-1][j-1];
int MaxSum=-INFINITY;//初始化
int imin,imax,jmin,jmax;
for(imin=1;imin<=N;imin++)
for(imax=imin;imax<=N;imax++)
for(jmin=1;jmin<=M;jmin++)
for(jmax=jmin;jmax<=M;jmax++)
MaxSum=MaxNum(MaxSum,PartSum[imax][jmax]-PartSum[imin-1][jmax]-PartSum[imax][jmin-1]+PartSum[imin-1][jmin-1]);
return MaxSum;
}时间复杂度是O(N^2*M^2)。这个复杂度还可以继续降低,用DP来做,我们把每一列看成一个元素,这样对于遍历的行区间,我们就可以当成一维来做。
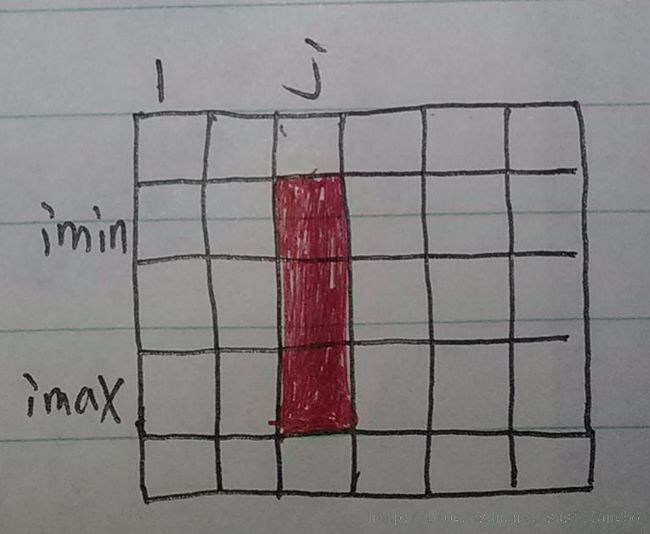
对于imin和imax之间的每一列,就相当于一维的一个元素。假设这个一维数组是BC,则BC[j]=array[imin][j]+....+array[imax][j],问题就变成了求BC数组的连续子数组之和的最大值了。而根据刚才求的部分和,我们可以知道对于imin行和imax行之间的区间第j列的值是 BC(PartSum,imin,imax,j)=PartSum[imax][j]-PartSum[imin-1][j]-PartSum[imax][j-1]+PartSum[imin-1][j-1]。// MaxMatrix.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include <iostream>
#include <limits>
using namespace std;
#define N 4
#define M 3
int BC(int (*PartSum)[M+1],int imin,int imax,int j) //imin--imax第j列的和
{
int value;
value=PartSum[imax][j]-PartSum[imin-1][j]-PartSum[imax][j-1]+PartSum[imin-1][j-1];
return value;
}
//求二维数组的连续子数组之和的最大值
int MaxSum(int (*array)[M])
{
int PartSum[N+1][M+1];
int i,j;
for(i=0;i<=N;i++)
PartSum[i][0]=0;
for(j=0;j<=M;j++)
PartSum[0][j]=0;
for(i=1;i<=N;i++)
for(j=1;j<=M;j++)
PartSum[i][j]=PartSum[i-1][j]+PartSum[i][j-1]-PartSum[i-1][j-1]+array[i-1][j-1];
int MaxSum=INT_MIN;
int Start,All;
int imin,imax;
for(imin=1;imin<=N;imin++)
{
for(imax=imin;imax<=N;imax++)
{
Start=BC(PartSum,imin,imax,M);
All=BC(PartSum,imin,imax,M);
for(j=M-1;j>=1;j--)
{
if(Start>0)
Start+=BC(PartSum,imin,imax,j);
else
Start=BC(PartSum,imin,imax,j);
if(Start>All)
All=Start;
}
if(All>MaxSum)
MaxSum=All;
}
}
return MaxSum;
}
int _tmain(int argc, _TCHAR* argv[])
{
int a[N][M]={
1,2,3,
4,0,-2,
-8,2,2,
9,3,-4
};
int maxSum=MaxSum(a);
cout<<maxSum<<endl;
getchar();
return 0;
}时间复杂度降到O(N*N*min(M,N)),差不多O(N^3)吧。