《机器学习》 KNN算法
《机器学习》 第八章 基于实例的学习
k-近邻算法 学习笔记
1.用途:
KNN算法主要用来分类。
2.概述和核心思想:
概述为一句话即为:
对于每个新实例,找出训练集(x(x为n维向量,x^n代表n维空间),y)空间中最靠近它的k个点,找出这k个点中出现次数最多的y值,将这个y值赋值给新实例的输出,从而以y取值的不同来分类。
思路与梯度下降的区别:
基于实例,顾名思义,这里的实例即训练集是已经知道输入参数x(多维向量),y=f(x),y也已知道,但是f(x)未知。
而既然是基于实例,前提则是训练集足够大。
因此可以使得KNN不用形成关于目标函数 f(x) 的明确函数公式,这点和之前的梯度下降算法有本质的区别:
梯度下降算法本质是在寻找公式,先自己假定一个函数,比如线性公式 y=f(x)=c0*x0+c1*c1 梯度下降的训练集虽然也是已经输入x和输出y。
但是梯度下降算法的思想是在寻找合适的c0,c1来明确化 目标函数。
而KNN不需要明确的目标函数公式,这点上KNN显得比较高帅富。
3.
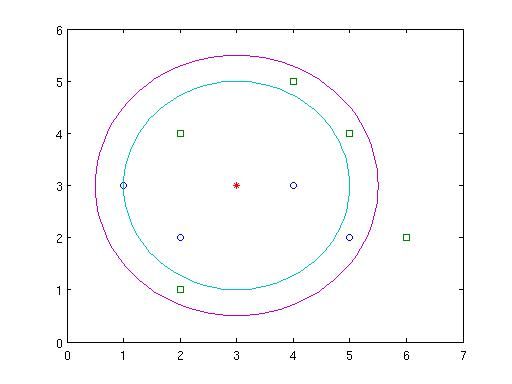
如下图,A类点为圆圈(假设y=0),B类点为方形(假设y=1),新实例点C为中间红色星号。
当k=4时,如下蓝色圆圈内的4个点,其中有A点3个,B点1个,故得y=f(C)=0,即归为A类。
当k=8时,A点和B点都是4个,所以C类归为A类或者B类都行,见仁见智。
当k>8时,显然C类归为B类。
上图由如下matlab代码画出
ax=[1,2,4,5]; ay=[3,2,3,2]; bx=[2,2,6,4,5]; by=[1,4,2,5,4]; r1=2; r2=2.5; cposx=3; cposy=3; alpha=0:pi/50:2*pi; c1x=r1*cos(alpha)+cposx; c1y=r1*sin(alpha)+cposy; c2x=r2*cos(alpha)+cposx; c2y=r2*sin(alpha)+cposy; plot(ax,ay,'o',bx,by,'s',3,3,'*',c1x,c1y,'-',c2x,c2y,'-') axis([0 7 0 6])
4.距离加权最近邻算法
上面的归类法有很明显的弊端,即每个点对新实例的归类的贡献值没有区别,这显然不合常理。
所以这里加入改进,将每个点对新实例的贡献值和距离相关,成反比的关系。
这里需要注意k值的意义:
当k值取训练集数量n的时候,则为查询一个新实例时候考虑所有样例,此时称为全局法,全局法的弊端是时间消耗。
如果仅考虑最靠近的样例,则为局部法。
5.关于KNN算法的几个要点:
*健壮性:
当给定训练集合足够大时可以消除孤立噪声。
*维度灾难:
样例每一维代表每一个属性,多维构成欧式空间,所以在分类时考虑了每一维,即每个属性都考虑了。
这点和决策树有明显不同。决策树是在每个分叉选择出最有分类能力的属性来作为分类假设。
分类时考虑全属性很可能会带来维度灾难,因为有可能每个属性对于分类的贡献不同,比如20个属性,其中只有2个属性和分类有关时。
解决方法:
将每个维度在计算距离时乘上一个贡献度参数。至于这个参数的选取又是一个机器学习的过程,大概是用交叉验证的方法。
*高效索引问题:
因为KNN算法是每次进来一个新实例时候才开始进行大量计算,所以有时候为了实时性,需要对已知样例建立索引,以便查找最近邻的时间开销足够小。
用到的一种索引方法是kd-tree:
将实例存储为树的叶子节点,邻近的实例存储在附近的节点。