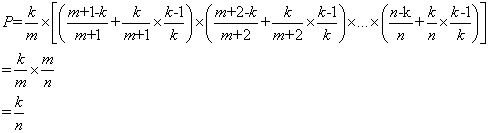蓄水池抽样——《编程珠玑》读书笔记

        问题：如何随机从n个对象中选择一个对象，这n个对象是按序排列的，但是在此之前你是不知道n的值的。

        思路：如果我们知道n的值，那么问题就可以简单的用一个大随机数rand()%n得到一个确切的随机位置，那么该位置的对象就是所求的对象，选中的概率是1/n。

        但现在我们并不知道n的值，这个问题便抽象为蓄水池抽样问题，即从一个包含n个对象的列表S中随机选取k个对象，n为一个非常大或者不知道的值。通常情况下，n是一个非常大的值，大到无法一次性把所有列表S中的对象都放到内存中。我们这个问题是蓄水池抽样问题的一个特例，即k=1。

        解法：我们总是选择第一个对象，以1/2的概率选择第二个，以1/3的概率选择第三个，以此类推，以1/m的概率选择第m个对象。当该过程结束时，每一个对象具有相同的选中概率，即1/n，证明如下。

        证明：第m个对象最终被选中的概率P=选择m的概率*其后面所有对象不被选择的概率，即

        对应的该问题的伪代码如下：

i = 0
while more input items
        with probability 1.0 / ++i
                choice = this input item
print choice

        C++代码实现如下：

#include <iostream>
#include <cstdlib>
#include <ctime>
#include <vector>

using namespace std;

typedef vector<int> IntVec;
typedef typename IntVec::iterator Iter;
typedef typename IntVec::const_iterator Const_Iter;

// generate a random number between i and k,
// both i and k are inclusive.
int randint(int i, int k)
{
	if (i > k)
	{
		int t = i; i = k; k = t; // swap
	}
	int ret = i + rand() % (k - i + 1);
	return ret;
}

// take 1 sample to result from input of unknown n items.
bool reservoir_sampling(const IntVec &input, int &result)
{
	srand(time(NULL));
	if (input.size() <= 0)
		return false;

	Const_Iter iter = input.begin();
	result = *iter++;
	for (int i = 1; iter != input.end(); ++iter, ++i)
	{
		int j = randint(0, i);
		if (j < 1)
			result = *iter;	
	}
	return true;
}

int main()
{
	const int n = 10;
	IntVec input(n);
	int result = 0;

	for (int i = 0; i != n; ++i)
		input[i] = i;
	if (reservoir_sampling(input, result))
		cout << result << endl;
	return 0;
}

        对应蓄水池抽样问题，可以类似的思路解决。先把读到的前k个对象放入“水库”，对于第k+1个对象开始，以k/(k+1)的概率选择该对象，以k/(k+2)的概率选择第k+2个对象，以此类推，以k/m的概率选择第m个对象（m>k）。如果m被选中，则随机替换水库中的一个对象。最终每个对象被选中的概率均为k/n，证明如下。

        证明：第m个对象被选中的概率=选择m的概率*（其后元素不被选择的概率+其后元素被选择的概率*不替换第m个对象的概率），即

        蓄水池抽样问题的伪代码如下：

array S[n];    //source, 0-based
array R[k];    // result, 0-based
integer i, j;

// fill the reservoir array
for each i in 0 to k - 1 do
        R[i] = S[i]
done;

// replace elements with gradually decreasing probability
for each i in k to n do
        j = random(0, i);   // important: inclusive range
        if j < k then
                R[j] = S[i]
        fi
done

        C++代码实现如下，该版本假设n知道，但n非常大：

#include <iostream>
#include <cstdlib>
#include <ctime>

using namespace std;

// generate a random number between i and k,
// both i and k are inclusive.
int randint(int i, int k)
{
	if (i > k)
	{
		int t = i; i = k; k = t; // swap
	}
	int ret = i + rand() % (k - i + 1);
	return ret;
}

// take m samples to result from input of n items.
bool reservoir_sampling(const int *input, int n, int *result, int m)
{
	srand(time(NULL));
	if (n < m || input == NULL || result == NULL)
		return false;
	for (int i = 0; i != m; ++i)
		result[i] = input[i];

	for (int i = m; i != n; ++i)
	{
		int j = randint(0, i);
		if (j < m)
			result[j] = input[i];	
	}
	return true;
}

int main()
{
	const int n = 100;
	const int m = 10;
	int input[n];
	int result[m];

	for (int i = 0; i != n; ++i)
		input[i] = i;
	if (reservoir_sampling(input, n, result, m))
		for (int i = 0; i != m; ++i)
			cout << result[i] << " ";
	cout << endl;
	return 0;
}

        下面这个程序假设不知道n的大小

#include <iostream>
#include <cstdlib>
#include <ctime>
#include <vector>

using namespace std;

typedef vector<int> IntVec;
typedef typename IntVec::iterator Iter;
typedef typename IntVec::const_iterator Const_Iter;

// generate a random number between i and k,
// both i and k are inclusive.
int randint(int i, int k)
{
	if (i > k)
	{
		int t = i; i = k; k = t; // swap
	}
	int ret = i + rand() % (k - i + 1);
	return ret;
}

// take m samples to result from input of n items.
bool reservoir_sampling(const IntVec &input, IntVec &result, int m)
{
	srand(time(NULL));
	if (input.size() < m)
		return false;

	result.resize(m);
	Const_Iter iter = input.begin();
	for (int i = 0; i != m; ++i)
		result[i] = *iter++;

	for (int i = m; iter != input.end(); ++i, ++iter)
	{
		int j = randint(0, i);
		if (j < m)
			result[j] = *iter;
	}
	return true;
}

int main()
{
	const int n = 100;
	const int m = 10;
	IntVec input(n), result(m);

	for (int i = 0; i != n; ++i)
		input[i] = i;
	if (reservoir_sampling(input, result, m))
		for (int i = 0; i != m; ++i)
			cout << result[i] << " ";
	cout << endl;
	return 0;
}

        本文参考：

http://www.cnblogs.com/HappyAngel/archive/2011/02/07/1949762.html

http://en.wikipedia.org/wiki/Reservoir_sampling

http://en.wikipedia.org/wiki/Fisher-Yates_shuffle