最小生成树

　设G = (V,E)是无向连通带权图，即一个网络。E中的每一条边（v,w）的权为c[v][w]。如果G的子图G’是一棵包含G的所有顶点的树，则称G’为G的生成树。生成树上各边权的总和称为生成树的耗费。在G的所有生成树中，耗费最小的生成树称为G的最小生成树。构造最小生成树的两种方法：Prim算法和Kruskal算法。

　　一、最小生成树的性质

　　设G = (V,E)是连通带权图，U是V的真子集。如果(u,v)∈E,且u∈U,v∈V-U,且在所有这样的边中，(u,v)的权c[u][v]最小，那么一定存在G的一棵最小生成树，它意(u,v)为其中一条边。这个性质有时也称为MST性质。

　　二、Prim算法

　　设G = (V,E)是连通带权图，V = {1,2,…,n}。构造G的最小生成树Prim算法的基本思想是：首先置S = {1}，然后，只要S是V的真子集，就进行如下的贪心选择：选取满足条件i ∈S,j ∈V – S,且c[i][j]最小的边，将顶点j添加到S中。这个过程一直进行到S = V时为止。在这个过程中选取到的所有边恰好构成G的一棵最小生成树。

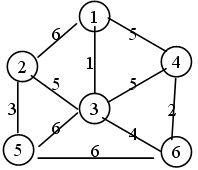
如下带权图：

生成过程：

1 -> 3 : 1

3 -> 6 : 4

6 -> 4: 2

3 -> 2 : 5

2 -> 5 : 3

 prim算法的演示如下：

http://sjjp.tjuci.edu.cn/sjjg/DataStructure/DS/web/flashhtml/prim.htm

/* 主题：贪心算法——最小生成树（Prim）
* 作者：chinazhangjie
* 邮箱：[email protected]
* 开发语言： C++
* 开发环境： Virsual Studio 2005
* 时间: 2010.11.30
*/

#include <iostream>
#include <vector>
#include <limits>
using namespace std ;

struct TreeNode
{
public:
    TreeNode (int nVertexIndexA = 0, int nVertexIndexB = 0, int nWeight = 0)
        : m_nVertexIndexA (nVertexIndexA),
        m_nVertexIndexB (nVertexIndexB),
        m_nWeight (nWeight)
    { }
public:
    int m_nVertexIndexA ;
    int m_nVertexIndexB ;
    int m_nWeight ;
} ;

class MST_Prim
{
public:
    MST_Prim (const vector<vector<int> >& vnGraph) 
    {
        m_nvGraph = vnGraph ;
        m_nNodeCount = (int)m_nvGraph.size () ;
    }
    void DoPrim ()
    {
        // 是否被访问标志
        vector<bool> bFlag (m_nNodeCount, false) ;
        bFlag[0] = true ;

        int nMaxIndexA ;
        int nMaxIndexB ;
        int j = 0 ;
        while (j < m_nNodeCount - 1) {
            int nMaxWeight = numeric_limits<int>::max () ;
            // 找到当前最短路径
            int i = 0 ;
            while (i < m_nNodeCount) {
                if (!bFlag[i]) {
                    ++ i ;
                    continue ;
                }
                for (int j = 0; j < m_nNodeCount; ++ j) {
                    if (!bFlag[j] && nMaxWeight > m_nvGraph[i][j]) {
                        nMaxWeight = m_nvGraph[i][j] ;
                        nMaxIndexA = i ;
                        nMaxIndexB = j ;
                    } 
                }
                ++ i ;
            }
            bFlag[nMaxIndexB] = true ;
            m_tnMSTree.push_back (TreeNode(nMaxIndexA, nMaxIndexB, nMaxWeight)) ;
            ++ j ;
        }
        // 输出结果
        for (vector<TreeNode>::const_iterator ite = m_tnMSTree.begin() ;
                ite != m_tnMSTree.end() ;
                ++ ite ) {
            cout << (*ite).m_nVertexIndexA << "->" 
                << (*ite).m_nVertexIndexB << " : "
                << (*ite).m_nWeight << endl ;
        }
    }
private:
    vector<vector<int> > m_nvGraph ;    // 无向连通图
    vector<TreeNode>    m_tnMSTree ;    // 最小生成树
    int    m_nNodeCount ;
} ;

int main()
{
    const int cnNodeCount = 6 ;
    vector<vector<int> > graph (cnNodeCount) ;
    for (size_t i = 0; i < graph.size() ; ++ i) {
        graph[i].resize (cnNodeCount, numeric_limits<int>::max()) ;
    }
    graph[0][1]= 6 ;
    graph[0][2] = 1 ;
    graph[0][3] = 5 ;
    graph[1][2] = 5 ;
    graph[1][4] = 3 ;
    graph[2][3] = 5 ;
    graph[2][4] = 6 ;
    graph[2][5] = 4 ;
    graph[3][5] = 2 ;
    graph[4][5] = 6 ;
    
    graph[1][0]= 6 ;
    graph[2][0] = 1 ;
    graph[3][0] = 5 ;
    graph[2][1] = 5 ;
    graph[4][1] = 3 ;
    graph[3][2] = 5 ;
    graph[4][2] = 6 ;
    graph[5][2] = 4 ;
    graph[5][3] = 2 ;
    graph[5][4] = 6 ;

    MST_Prim mstp (graph) ;
    mstp.DoPrim () ;
     return 0 ;
}

　三、Kruskal算法

　　当图的边数为e时，Kruskal算法所需的时间是O(eloge)。当e = Ω(n^2)时，Kruskal算法比Prim算法差；但当e = o(n^2)时，Kruskal算法比Prim算法好得多。

给定无向连同带权图G = (V,E),V = {1,2,...,n}。Kruskal算法构造G的最小生成树的基本思想是：

（1）首先将G的n个顶点看成n个孤立的连通分支。将所有的边按权从小大排序。

（2）从第一条边开始，依边权递增的顺序检查每一条边。并按照下述方法连接两个不同的连通分支：当查看到第k条边(v,w)时，如果端点v和w分别是当前两个不同的连通分支T1和T2的端点是，就用边(v,w)将T1和T2连接成一个连通分支，然后继续查看第k+1条边；如果端点v和w在当前的同一个连通分支中，就直接再查看k+1条边。这个过程一个进行到只剩下一个连通分支时为止。

此时，已构成G的一棵最小生成树。

Kruskal算法的选边过程：

1 -> 3 : 1

4 -> 6 : 2

2 -> 5 : 3

3 -> 4 : 4

2 -> 3 : 5

/* 主题：贪心算法之最小生成树(Kruskal算法)
* 作者：chinazhangjie
* 邮箱：[email protected]
* 开发语言：C++
* 开发环境：Visual Studio 2005
* 时间：2010.12.01
*/

#include <iostream>
#include <vector>
#include <queue>
#include <limits>
using namespace std ;

struct TreeNode
{
public:
    TreeNode (int nVertexIndexA = 0, int nVertexIndexB = 0, int nWeight = 0)
        : m_nVertexIndexA (nVertexIndexA),
        m_nVertexIndexB (nVertexIndexB),
        m_nWeight (nWeight)
    { }
    friend 
    bool operator < (const TreeNode& lth, const TreeNode& rth) 
    {
        return lth.m_nWeight > rth.m_nWeight ;
    }

public:
    int m_nVertexIndexA ;
    int m_nVertexIndexB ;
    int m_nWeight ;
} ;

//  并查集
class UnionSet 
{
public:
    UnionSet (int nSetEleCount)
        : m_nSetEleCount (nSetEleCount)
    {
        __init() ;
    }
    // 合并i，j。如果i，j同在集合中，返回false。否则返回true
    bool Union (int i, int j)
    {
        int ifather = __find (i) ;
        int jfather = __find (j) ;
        if (ifather == jfather )
        {
            return false ;
            // copy (m_nvFather.begin(), m_nvFather.end(), ostream_iterator<int> (cout, " "));
            // cout << endl ;
        }
        else
        {
            m_nvFather[jfather] = ifather ;
            // copy (m_nvFather.begin(), m_nvFather.end(), ostream_iterator<int> (cout, " "));
            // cout << endl ;
            return true ;
        }
        
    }

private:
    // 初始化并查集
    int __init()
    {
        m_nvFather.resize (m_nSetEleCount) ;
        for (vector<int>::size_type i = 0 ;
            i < m_nSetEleCount;
            ++ i )
        {
            m_nvFather[i] = static_cast<int>(i) ;
            // cout << m_nvFather[i] << " " ;
        }
        // cout << endl ;
        return 0 ;
    }
    // 查找index元素的父亲节点 并且压缩路径长度 
    int __find (int nIndex)
    {
        if (nIndex == m_nvFather[nIndex])
        {
            return nIndex;
        }
        return  m_nvFather[nIndex] = __find (m_nvFather[nIndex]);
    }

private:
    vector<int>                m_nvFather ;    // 父亲数组
    vector<int>::size_type m_nSetEleCount ;    // 集合中结点个数
} ;

class MST_Kruskal
{
    typedef priority_queue<TreeNode> MinHeap ;
public:
    MST_Kruskal (const vector<vector<int> >& graph) 
    {
        m_nNodeCount = static_cast<int>(graph.size ()) ;
        __getMinHeap (graph) ;
    }
    void DoKruskal ()
    {
        UnionSet us (m_nNodeCount) ;
        int k = 0 ; 
        while (m_minheap.size() != 0 && k < m_nNodeCount - 1) 
        {
            TreeNode tn = m_minheap.top () ;
            m_minheap.pop () ;
            // 判断合理性
            if (us.Union (tn.m_nVertexIndexA, tn.m_nVertexIndexB)) 
            {
                m_tnMSTree.push_back (tn) ;
                ++ k ;
            }
        }
        // 输出结果
        for (size_t i = 0; i < m_tnMSTree.size() ; ++ i) 
        {
            cout << m_tnMSTree[i].m_nVertexIndexA << "->"
                << m_tnMSTree[i].m_nVertexIndexB << " : "
                << m_tnMSTree[i].m_nWeight 
                << endl ;
        }
    }

private:
    void __getMinHeap (const vector<vector<int> >& graph) 
    {
        for (int i = 0; i < m_nNodeCount; ++ i) 
        {
            for (int j = 0; j < m_nNodeCount; ++ j) 
            {
                if (graph[i][j] != numeric_limits<int>::max()) 
                {
                    m_minheap.push (TreeNode(i, j, graph[i][j])) ;
                }
            }
        }
    }
private:
    vector<TreeNode>    m_tnMSTree ;
    int                    m_nNodeCount ;
    MinHeap                m_minheap ;
} ;


int main ()
{
    const int cnNodeCount = 6 ;
    vector<vector<int> > graph (cnNodeCount) ;
    for (size_t i = 0; i < graph.size() ; ++ i) 
    {
        graph[i].resize (cnNodeCount, numeric_limits<int>::max()) ;
    }
    graph[0][1]= 6 ;
    graph[0][2] = 1 ;
    graph[0][3] = 3 ;
    graph[1][2] = 5 ;
    graph[1][4] = 3 ;
    graph[2][3] = 5 ;
    graph[2][4] = 6 ;
    graph[2][5] = 4 ;
    graph[3][5] = 2 ;
    graph[4][5] = 6 ;
    
    graph[1][0]= 6 ;
    graph[2][0] = 1 ;
    graph[3][0] = 3 ;
    graph[2][1] = 5 ;
    graph[4][1] = 3 ;
    graph[3][2] = 5 ;
    graph[4][2] = 6 ;
    graph[5][2] = 4 ;
    graph[5][3] = 2 ;
    graph[5][4] = 6 ;

    MST_Kruskal mst (graph);
    mst.DoKruskal () ;
}