UVa OJ 105 - The Skyline Problem (地平线问题)
Time limit: 3.000 seconds
Background
With the advent of high speed graphics workstations, CAD (computer-aided design) and other areas (CAM, VLSI design) have made increasingly effective use of computers. One of the problems with drawing images is the elimination of hidden lines -- lines obscured by other parts of a drawing.
The Problem
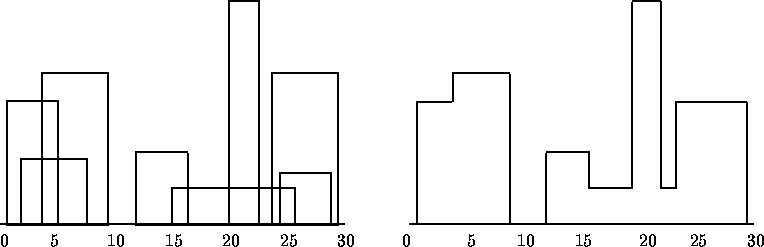
You are to design a program to assist an architect in drawing the skyline of a city given the locations of the buildings in the city. To make the problem tractable, all buildings are rectangular in shape and they share a common bottom (the city they are built in is very flat). The city is also viewed as two-dimensional. A building is specified by an ordered triple (Li, Hi, Ri) where Li and Ri are left and right coordinates, respectively, of building i and Hi is the height of the building. In the diagram below buildings are shown on the left with triples (1,11,5), (2,6,7), (3,13,9), (12,7,16), (14,3,25), (19,18,22), (23,13,29), (24,4,28)
the skyline, shown on the right, is represented by the sequence: (1, 11, 3, 13, 9, 0, 12, 7, 16, 3, 19, 18, 22, 3, 23, 13, 29, 0)
The Input
The input is a sequence of building triples. All coordinates of buildings are positive integers less than 10,000 and there will be at least one and at most 5,000 buildings in the input file. Each building triple is on a line by itself in the input file. All integers in a triple are separated by one or more spaces. The triples will be sorted by Li , the left x-coordinate of the building, so the building with the smallest left x-coordinate is first in the input file.
The Output
The output should consist of the vector that describes the skyline as shown in the example above. In the skyline vector (v1, v2, v3, ..., vn-2, vn-1, nv) , the vi such that i is an even number represent a horizontal line (height). The vi such that i is an odd number represent a vertical line (x-coordinate). The skyline vector should represent the "path" taken, for example, by a bug starting at the minimum x-coordinate and traveling horizontally and vertically over all the lines that define the skyline. Thus the last entry in the skyline vector will be a 0. The coordinates must be separated by a blank space.
Sample Input
1 11 5
2 6 7
3 13 9
12 7 16
14 3 25
19 18 22
23 13 29
24 4 28
Sample Output
1 11 3 13 9 0 12 7 16 3 19 18 22 3 23 13 29 0
Hint
这道题是简单题,由于限定的数据量很小,可以直接开一个横坐标数组,直接标定每一点的高度即可。但是如何使用尽可能小的内存和时间来完成就是一件值得思考的事了。我的思路是按输入的数据将图形分成从左至右,首尾相接的小段,这样就可以边输入边处理了,不用存储整个坐标轴的数据。当输入一个新的块时,从右向左依次判断与已有小段的相互位置关系,做相应的插入、更新操作。在循环每一个已有小段时,要保证新入的块与小段右对齐,如果没有对齐则进行分解插入。每处理完一轮就缩小新给的小段,使它再与下一个小段右对齐。
Analysis
#include <iostream>
#include <list>
using namespace std;
struct OUTLINE {
int nLeft;
int nRight;
int nHeight;
};
int main(void){
OUTLINE CurOL, NewOL;
list<OUTLINE> listSkyline;
cin >> CurOL.nLeft >> CurOL.nHeight >> CurOL.nRight;
listSkyline.push_front(CurOL);
while (cin >> CurOL.nLeft >> CurOL.nHeight >> CurOL.nRight) {
if (CurOL.nHeight <= listSkyline.front().nHeight &&
CurOL.nRight <= listSkyline.front().nRight) {
continue;
}
if (CurOL.nLeft > listSkyline.front().nRight) {
NewOL.nLeft = listSkyline.front().nRight;
NewOL.nRight = CurOL.nLeft;
NewOL.nHeight = 0;
listSkyline.push_front(NewOL);
}
for (list<OUTLINE>::iterator iPrev = listSkyline.begin();
iPrev != listSkyline.end(); ++iPrev) {
if (CurOL.nLeft == CurOL.nRight) {
break;
}
if (CurOL.nRight <= iPrev->nLeft) {
continue;
}
if (CurOL.nRight > iPrev->nRight) {
NewOL.nLeft = iPrev->nRight;
NewOL.nRight = CurOL.nRight;
NewOL.nHeight = CurOL.nHeight;
iPrev = listSkyline.insert(iPrev, NewOL);
CurOL.nRight = NewOL.nLeft;
continue;
}
if (CurOL.nRight < iPrev->nRight &&
CurOL.nHeight > iPrev->nHeight) {
NewOL.nLeft = CurOL.nRight;
NewOL.nRight = iPrev->nRight;
NewOL.nHeight = iPrev->nHeight;
iPrev->nRight = NewOL.nLeft;
iPrev = listSkyline.insert(iPrev, NewOL);
continue;
}
if (CurOL.nLeft > iPrev->nLeft) {
if (CurOL.nHeight > iPrev->nHeight) {
iPrev->nRight = CurOL.nLeft;
listSkyline.insert(iPrev, CurOL);
}
break;
}
if (CurOL.nHeight > iPrev->nHeight) {
iPrev->nHeight = CurOL.nHeight;
}
CurOL.nRight = iPrev->nLeft;
}
}
int nLastHeight = 0;
for (list<OUTLINE>::reverse_iterator ri = listSkyline.rbegin();
ri != listSkyline.rend(); ++ri) {
if (ri->nHeight != nLastHeight) {
cout << ri->nLeft << ' ' << ri->nHeight << ' ';
nLastHeight = ri->nHeight;
}
}
cout << listSkyline.front().nRight << " 0" << endl;
return 0;
}