0037算法笔记——【分支限界法】最大团问题

        问题描述

     给定无向图G=(V, E)，其中V是非空集合，称为顶点集；E是V中元素构成的无序二元组的集合，称为边集，无向图中的边均是顶点的无序对，无序对常用圆括号“( )”表示。如果U∈V，且对任意两个顶点u，v∈U有(u, v)∈E，则称U是G的完全子图(完全图G就是指图G的每个顶点之间都有连边)。G的完全子图U是G的团当且仅当U不包含在G的更大的完全子图中。G的最大团是指G中所含顶点数最多的团。

     如果U∈V且对任意u，v∈U有(u, v)不属于E，则称U是G的空子图。G的空子图U是G的独立集当且仅当U不包含在G的更大的空子图中。G的最大独立集是G中所含顶点数最多的独立集。

     对于任一无向图G=(V, E)，其补图G'=(V', E')定义为：V'=V，且(u, v)∈E'当且仅当(u, v)∈E。
     如果U是G的完全子图，则它也是G'的空子图，反之亦然。因此，G的团与G'的独立集之间存在一一对应的关系。特殊地，U是G的最大团当且仅当U是G'的最大独立集。

     例：如图所示，给定无向图G={V, E}，其中V={1,2,3,4,5}，E={(1,2), (1,4), (1,5),(2,3), (2,5), (3,5), (4,5)}。根据最大团(MCP)定义，子集{1,2}是图G的一个大小为2的完全子图，但不是一个团，因为它包含于G的更大的完全子图{1,2,5}之中。{1,2,5}是G的一个最大团。{1,4,5}和{2,3,5}也是G的最大团。右侧图是无向图G的补图G'。根据最大独立集定义，{2,4}是G的一个空子图，同时也是G的一个最大独立集。虽然{1,2}也是G'的空子图，但它不是G'的独立集，因为它包含在G'的空子图{1,2,5}中。{1,2,5}是G'的最大独立集。{1,4,5}和{2,3,5}也是G'的最大独立集。

     算法设计

      最大团问题的解空间树也是一棵子集树。子集树的根结点是初始扩展结点，对于这个特殊的扩展结点，其cliqueSize的值为0。 算法在扩展内部结点时，首先考察其左儿子结点。在左儿子结点处，将顶点i加入到当前团中，并检查该顶点与当前团中其它顶点之间是否有边相连。当顶点i与当前团中所有顶点之间都有边相连，则相应的左儿子结点是可行结点，将它加入到子集树中并插入活结点优先队列，否则就不是可行结点。

     接着继续考察当前扩展结点的右儿子结点。当upperSize>bestn时，右子树中可能含有最优解，此时将右儿子结点加入到子集树中并插入到活结点优先队列中。算法的while循环的终止条件是遇到子集树中的一个叶结点(即n+1层结点)成为当前扩展结点。
    对于子集树中的叶结点，有upperSize＝cliqueSize。此时活结点优先队列中剩余结点的upperSize值均不超过当前扩展结点的upperSize值，从而进一步搜索不可能得到更大的团，此时算法已找到一个最优解。

     算法具体实现如下：

     1、MaxHeap.h

template<class T>
class MaxHeap
{
	public:
		MaxHeap(int MaxHeapSize = 10);
		~MaxHeap() {delete [] heap;}
        int Size() const {return CurrentSize;}

        T Max() 
		{          //查
           if (CurrentSize == 0)
		   {
                throw OutOfBounds();
		   }
           return heap[1];
        }

		MaxHeap<T>& Insert(const T& x); //增
		MaxHeap<T>& DeleteMax(T& x);   //删

		void Initialize(T a[], int size, int ArraySize);

	private:
		int CurrentSize, MaxSize;
		T *heap;  // element array
};

template<class T>
MaxHeap<T>::MaxHeap(int MaxHeapSize)
{// Max heap constructor.
	MaxSize = MaxHeapSize;
	heap = new T[MaxSize+1];
	CurrentSize = 0;
}

template<class T>
MaxHeap<T>& MaxHeap<T>::Insert(const T& x)
{// Insert x into the max heap.
	if (CurrentSize == MaxSize)
	{
		cout<<"no space!"<<endl; 
		return *this; 
	}

    // 寻找新元素x的位置
    // i——初始为新叶节点的位置，逐层向上，寻找最终位置
	int i = ++CurrentSize;
	while (i != 1 && x > heap[i/2])
	{
		// i不是根节点，且其值大于父节点的值，需要继续调整
		heap[i] = heap[i/2]; // 父节点下降
		i /= 2;              // 继续向上，搜寻正确位置
    }

   heap[i] = x;
   return *this;
}

template<class T>
MaxHeap<T>& MaxHeap<T>::DeleteMax(T& x)
{// Set x to max element and delete max element from heap.
	// check if heap is empty
	if (CurrentSize == 0)
	{
		cout<<"Empty heap!"<<endl; 
		return *this; 
	}

	x = heap[1]; // 删除最大元素
	// 重整堆
	T y = heap[CurrentSize--]; // 取最后一个节点，从根开始重整

	// find place for y starting at root
	int i = 1,  // current node of heap
	   ci = 2; // child of i

	while (ci <= CurrentSize) 
    {
		// 使ci指向i的两个孩子中较大者
		if (ci < CurrentSize && heap[ci] < heap[ci+1])
		{
			ci++;
		}
		// y的值大于等于孩子节点吗？
		if (y >= heap[ci])
		{
			break;   // 是，i就是y的正确位置，退出
		}

		// 否，需要继续向下，重整堆
		heap[i] = heap[ci]; // 大于父节点的孩子节点上升
		i = ci;             // 向下一层，继续搜索正确位置
		ci *= 2;
    }

	heap[i] = y;
	return *this;
}

template<class T>
void MaxHeap<T>::Initialize(T a[], int size,int ArraySize)
{// Initialize max heap to array a.
	delete [] heap;
	heap = a;
	CurrentSize = size;
	MaxSize = ArraySize;

	// 从最后一个内部节点开始，一直到根，对每个子树进行堆重整
   for (int i = CurrentSize/2; i >= 1; i--)
   {
		T y = heap[i]; // 子树根节点元素
		// find place to put y
		int c = 2*i; // parent of c is target
                   // location for y
		while (c <= CurrentSize) 
		{
			// heap[c] should be larger sibling
			if (c < CurrentSize && heap[c] < heap[c+1])
			{
				c++;
			}
			// can we put y in heap[c/2]?
			if (y >= heap[c])
			{
				break;  // yes
			}

			// no
			heap[c/2] = heap[c]; // move child up
			c *= 2; // move down a level
        }
		heap[c/2] = y;
	}
}

     2、6d6.cpp

//最大团问题 优先队列分支限界法求解 
#include "stdafx.h"
#include "MaxHeap.h"
#include <iostream>
#include <fstream>
using namespace std;

const int N = 5;//图G的顶点数
ifstream fin("6d6.txt");   

class bbnode
{
	friend class Clique;
	private:
		bbnode *parent;		//指向父节点的指针
		bool LChild;		//左儿子节点标识
};

class CliqueNode
{
	friend class Clique;
	public:
		operator int() const
		{	
			return un;
		}
	private:
		int cn,			//当前团的顶点数
			un,			//当前团最大顶点数的上界
			level;		//节点在子集空间树中所处的层次
		bbnode *ptr;	//指向活节点在子集树中相应节点的指针
};

class Clique
{
	friend int main(void);
	public:
		int BBMaxClique(int []);
	private:
		void AddLiveNode(MaxHeap<CliqueNode>&H,int cn,int un,int level,bbnode E[],bool ch);
		int **a,		//图G的邻接矩阵
			n;			//图G的顶点数
};

int main()
{
	int bestx[N+1];
	int **a = new int *[N+1];  
    for(int i=1;i<=N;i++)    
    {    
        a[i] = new int[N+1];    
    } 
	
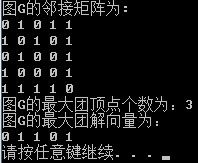
	cout<<"图G的邻接矩阵为:"<<endl;
	for(int i=1; i<=N; i++)  
    {  
        for(int j=1; j<=N; j++)  
        {  
            fin>>a[i][j];      
            cout<<a[i][j]<<" ";    
        }  
        cout<<endl;  
    }

	Clique c;
	c.a = a;
	c.n = N;

	cout<<"图G的最大团顶点个数为："<<c.BBMaxClique(bestx)<<endl;
	cout<<"图G的最大团解向量为："<<endl;
	for(int i=1;i<=N;i++)    
    {   
		cout<<bestx[i]<<" ";
    } 
	cout<<endl;

	for(int i=1;i<=N;i++)    
    {   
        delete[] a[i];   
    } 
	delete []a;
	return 0;
}

//将活节点加入到子集空间树中并插入到最大堆中
void Clique::AddLiveNode(MaxHeap<CliqueNode> &H, int cn, int un, int level, bbnode E[], bool ch)
{
	bbnode *b = new bbnode;
	b->parent = E;
	b->LChild = ch;

	CliqueNode N;
	N.cn = cn;
	N.ptr = b;
	N.un = un;
	N.level = level;
	H.Insert(N);
}

//解最大团问题的优先队列式分支限界法
int Clique::BBMaxClique(int bestx[])
{
	MaxHeap<CliqueNode> H(1000);

	//初始化
	bbnode *E = 0;
	int i = 1,
		cn = 0,
		bestn = 0;

	//搜集子集空间树
	while(i!=n+1)//非叶节点
	{
		//检查顶点i与当前团中其他顶点之间是否有边相连
		bool OK = true;
		bbnode *B = E;
		for(int j=i-1; j>0; B=B->parent,j--)
		{
			if(B->LChild && a[i][j]==0)
			{
				OK = false;
				break;
			}
		}

		if(OK)//左儿子节点为可行结点
		{
			if(cn+1>bestn)
			{
				bestn = cn + 1;
			}
			AddLiveNode(H,cn+1,cn+n-i+1,i+1,E,true);
		}

		if(cn+n-i>=bestn)//右子树可能含有最优解
		{
			AddLiveNode(H,cn,cn+n-i,i+1,E,false);
		}

		//取下一扩展节点
		CliqueNode N;
		H.DeleteMax(N); //堆非空
		E = N.ptr;
		cn = N.cn;
		i = N.level;
	}

	//构造当前最优解
	for(int j=n; j>0; j--)
	{
		bestx[j] = E->LChild;
		E = E->parent;
	}

	return bestn;
}